利用T矩阵法实现大衰减量的测量

闫道广　陈志宇

(1.北京理工大学，北京 100081；2.中国人民解放军92493部队，葫芦岛 125000)

0　引言

微波衰减是无线电计量最为基础的参量之一，其用来表征无线电信号的幅度在传输过程中减弱的程度，是各种传输线、电子元器件、电子设备及系统的传输特性[1-2]。现有的微波衰减计量测试手段，由于隔离衰减器占用了部分动态范围，真正可用量程最高达到90dB，在毫米波段甚至量程更低，即使采用高灵敏度的接收机也很难实现大衰减量的精确测量。然而，目前Agilent、R/S、Anritsu、Weinschel等主流微波厂商出品的可变衰减器量程都已达到110dB甚至更高，现有的测试手段已不能满足测试需求[3]。为解决大衰减量的计量测试问题，通过对基础测试理论的分析研究，提出了利用T矩阵法实现大衰减量间接测量的技术方案。

1　微波网络参数模型[4-6]

在对微波网络进行分析研究时，常常利用散射参量、传输参量、电路参量等，而应用最广泛且具有良好的可测性的是散射参量，即我们所熟悉的S参数。而传输参量不像散射参量那样全部具有明确的物理意义，也不方便测量，但是散射参量却有一个非常好的特性——级联特性。当网络由两个或多个网络级联而成时，使用传输参量矩阵进行表征和分析更为方便。而研究具有大衰减量的步进可变衰减器的测量问题时，即可将其看作由多个不同衰减量的衰减器级联而成。

对于一个线性无源二端口网络，如图1所示，设a1、b1为端口1的入射波和反射波电压，a2、b2为端口2的入射波和反射波电压，则二端口网络的传输特性可由式(1)表征。其中T参数矩阵即为网络的传输参量，具体定义如式(2)所示。

(1)

(2)

图1　使用T参数描述线性无源二端口网络

式中，T11表示端口2接匹配负载(a2=0)时，端口1到端口2的传输系数的倒数，T22表示端口2无反射输出(b2=0)时，端口2到端口1的传输系数，其余参量无明确的物理意义。

T参量的级联特性表现为，当多个线性无源的二端口网络连接后，总的T参量等于各个二端口网络T参量的乘积，如式(3)所示。

[T]=[T1]·[T2]·……·[Tn]

(3)

利用这个性质，只要预先测得步进可变衰减器中的分衰减器的T参量即可计算得出总的T参量。为此需要寻求T参量与可测参量S参数的关系。

散射参量是表征微波网络端口参考面处的入射波和输出波之间关系的量，是开展微波网络外特性研究应用最为广泛的参量形式。散射参量一般用S参数矩阵进行描述，一个线性无源二端口网络可用式(4)进行表征。

(4)

(5)

其中，S11、S21表示端口2接匹配负载(a2=0)时，端口1的反射系数及端口1到端口2的传输系数；S22、S12表示端口1接匹配负载(a1=0)时，端口2的反射系数及端口2到端口1的传输系数。S参数仅与网络本身的性质有关，与外界因素无关。

对于二端口网络T参数和S参数可以通过式(6)进行转化。

(6)

2　T矩阵法测量大衰减量的测试原理

以Agilent公司的步进式程控可变衰减器84906L为例，其为机械电阻式步进衰减器，衰减量程从0～90dB，频率范围DC～50GHz。衰减器的内部结构如图2所示，在衰减器内部由4个分衰减器连接而成，分别是10dB、20dB和2个30dB。当需要输出不同的衰减量时，可通过表1选择不同的分衰减器组合而成。

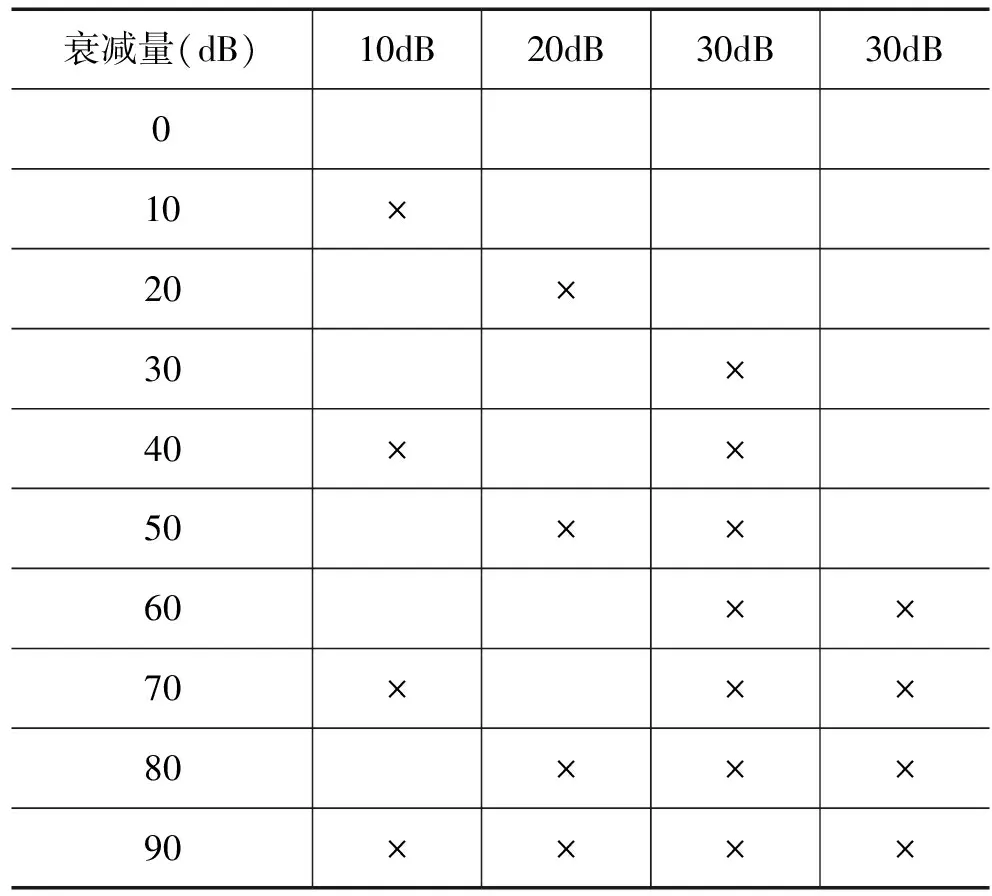
表1　衰减量内部组合表

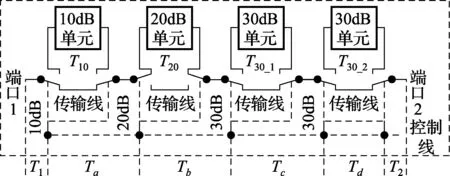
图2　84906L可变衰减器的内部结构

设Ta、Tb、Tc、Td分别是各个分衰减器短接时的T参数，T1、T2分别是端口1和端口2的连接部分的T参数，T0_m、T10_m、T20_m、T30_1_m、T30_2_m分别是84906L直接输出0dB、10dB、20dB、30dB_1、30dB_2时的T参数，根据T参数的级联特性，可以推导出各个分衰减器的T矩阵参数(T10、T20、T30_1、T30_2)，如式(7)所示。

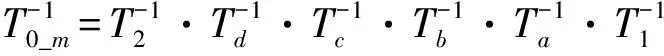
(7)

同样根据T矩阵的级联特性，以设定90dB的衰减量为例，此时要求所有分衰减器全部选通，总的T矩阵(T90_m)等于各个分衰减器的T矩阵(T10、T20、T30_1、T30_2)及输入输出端口的T矩阵(T1、T2)的乘积，如式(8)所示，经过推导，可以得出T90_m与T0_m、T10_m、T20_m、T30_1_m、T30_2_m之间的确定关系，而后者可以通过精确测量的分衰减器S参数转化得出，即T90_m可以通过精确测量值推导得出，从而在经过转化得出相应的S参数，得出90dB时的精确衰减量值[7]。类似的，其它衰减量值点也可通过相应的推导计算得出，如表2所示。

T90_m=T1·T10·T20·T30_1·T30_2·T2

·T30_2_m

(8)

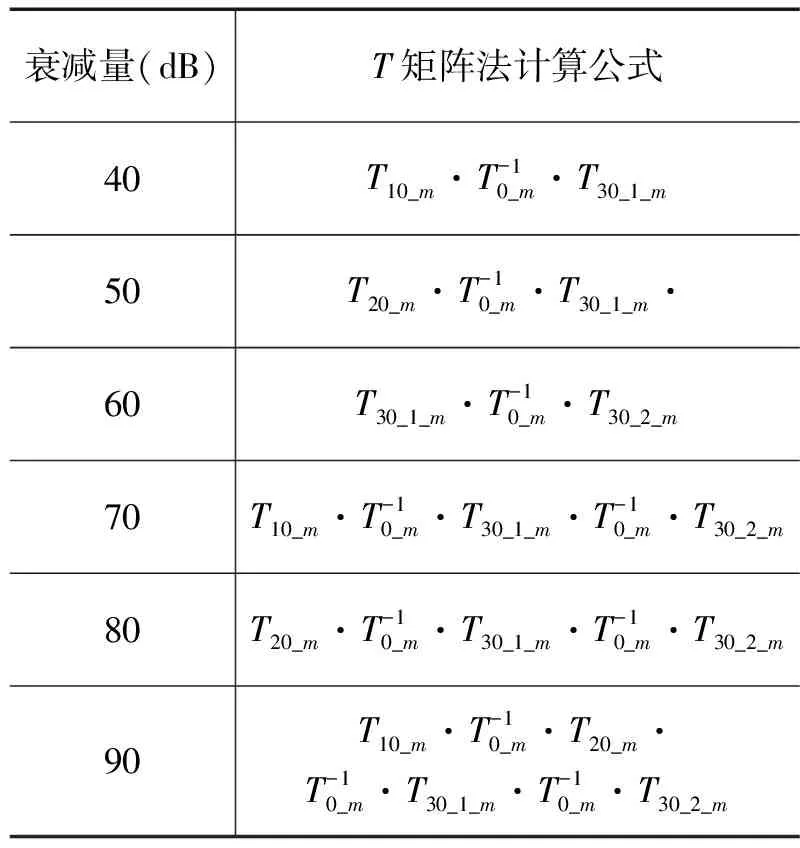
表2　不同衰减量计算公式一览表

3　实测验证

为验证方法的可行性，使用N5230A矢量网络分析仪对84906L程控可变衰减器的全部S参数进行了测量，使用T矩阵法进行运算，结果同上级给定的计量值进行比较，如图3所示，结果表明一致性比较好。

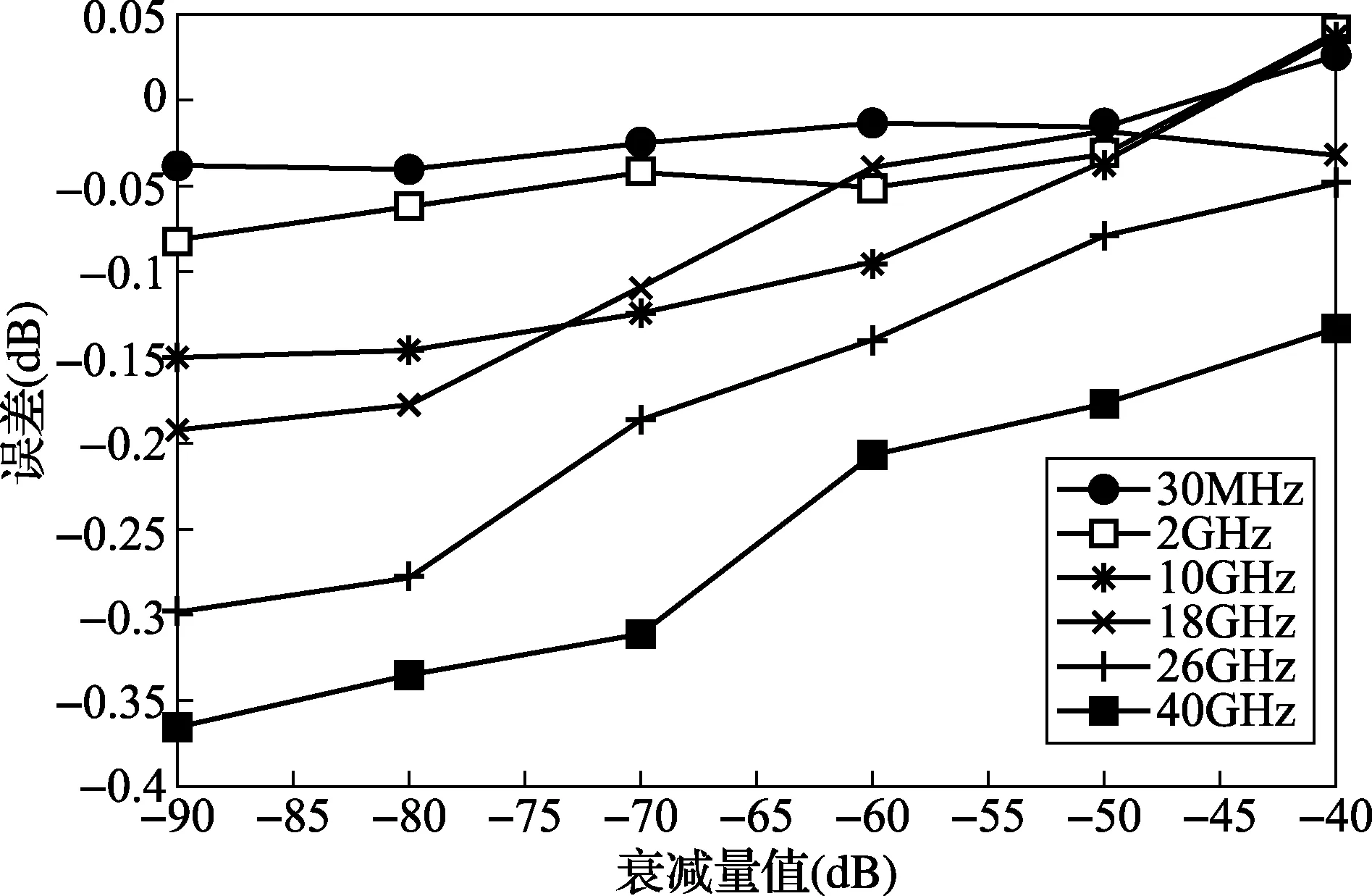
图3　T矩阵法结果与上级计量值误差比较图

4　结束语

利用T矩阵法实现大衰减量测试的理论依据充分，实际测试结果也验证了技术可行性。经过误差传递理论的推导， 在90dB时的不确定度约为0.3dB左右，满足一般的计量测试需求。只是T矩阵法的计算过程涉及到大量的复数矩阵运算，需要使用Matlab等专门的数学运算工具才容易实现，若使用一般的编程工具或计算手段则运算量相当大。对于非程控的可变衰减器来说，由于不能任意选定分衰减器的输出，需要另行研究。综合来看，T矩阵法对于实现大衰减量的计量测试具有十分广泛的应用前景[8]。

[1]冯新善.无线电基本参量[M].北京：中国计量出版社，1987

[2]国防科工委科技与质量司.无线电电子学计量[M].北京：原子能出版社，2002

[3]黄志洵，曲敏.微波衰减测量技术的进展[J].中国传媒大学学报(自然科学版)，2010，17(1)

[4]Kilby，G.J.，Smith，T.A.J.and Warner，F.L.The accurate measurement of high attenuation at radio frequencies[J].Instrumentation and Measurement，IEEE Transactions on，1995，44(2):308-311.

[5]Warner，F.L.High accuracy，150 dB，attenuation measurement system for traceability at radio frequencies [C].What’s New in Microwave Measurements，IEE Colloquium on，1990.

[6]尚洪臣.微波网络[M].南京：东南大学出版社，1996

[7]Sulan Zhang.High Attenuation Measurement of Step Attenuators [C].NCSLI,2010.

[8]闫润卿，李英慧.微波技术基础[M].北京：北京理工大学出版社，2004