螺纹单一中径的三针和量球法测量公式讨论

刘远模

(成都艾立特螺纹工具有限公司 ， 成都 610512)

0　引言

本文详细讨论了螺纹单一中径的三针和量球法测量公式，对欧洲广泛使用的Berndt公式以及国内专家苏宗康先生的公式其差异进行分析，论证了Berndt公式的成立条件和苏氏公式理论上的缺陷，并与本文作者文献[6]公式比较，最后用计算示例进行了验证。

1　Berndt计算公式讨论

对欧盟和世界都有很大影响的Berndt公式的研究是很有必要的。

1.1　Berndt公式

由欧盟认证的用机械测头测定圆柱螺纹量规中径指南(EA Guidelines on the Determination of Pitch Diameter of Parallel Thread Gauges by Mechanical Probing) EA-10/10在给定实测值m情况下用下式计算被测螺纹中径d2(外螺纹)或D2(内螺纹)[1]

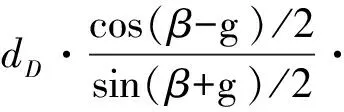
(1)

辅助角θ用下式进行迭代计算

(2)

初始值为

(3)

1.2　讨论

1.2.1Berndt公式的成立条件

在式(1)、(2)右端有根式，如果根号值为负则根式不成立，即前两式不成立。由式(1)、(2)的根式有

sinθ≤dD/mcos(β-g )/2

(4)

如果满足式(4)，那么式(1)、(2)成立。否则两公式不成立。

1.2.2式(2)的讨论

由式(2)为

(5)

如果θk-1=0，则由式(5)中θk远小于1，θk=arcsin(θk)代入式(2)获得式(3)。这样用θ=0代入式(5)迭代运算即可获得准确θ值。把此值代入式(1)计算中径尺寸而没有必要再用式(3)计算辅助角的初始值θ1。

如果用sin(θk)代替arcsin(θk)，从计算结果可知θ变化不足以带来结果(d2或m)达到0.1μm变化。

1.2.3已知中径求三针测量的跨线测量值或求量球跨球测量值m(即检验计算)

由式(1)可得

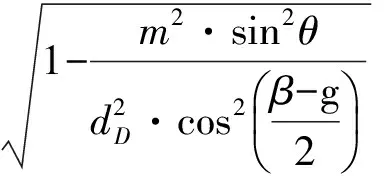
(6)

令θ=0则

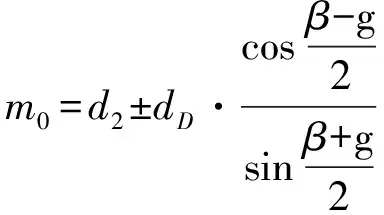
(6a)

以θ=0和m0为初始值，迭代运算式(5)和(6)求得θ和m。

1.2.4斜置误差计算

V型圆环槽是θ=0时螺纹的特例，此时由式(1)所得中径用加注脚“0”表示，即

(7)

为了叙述简便下面一律用d2或d20包含内外螺纹中径。

斜置误差Δ为

Δ=m-m0

(8)

Δ=d20-d2

(9)

式(8)用于检验计算，用式(6)和(6a)值代入计算。式(9)用于测试计算(即已知测量值求中径)，用式(1)和式(7)值代入计算。

1.2.5 对称螺纹计算

对于对称螺纹，β=g =α/2，于是式(1)、(5)分别为

(10)

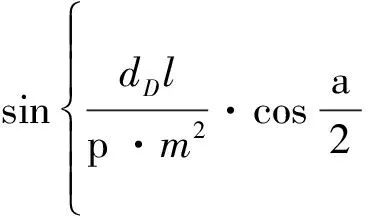
(11)

用θ=0作为迭代初始值代入式(11)进行迭代运算，将所得代入式(10)计算中径。

由式(4)可知，式(10)、(11)成立条件为

sinθ≤dD/m

(12)

由式(7)得

(13)

测试计算的斜置误差按式(9)计算。

由式(6)和(6a)分别得

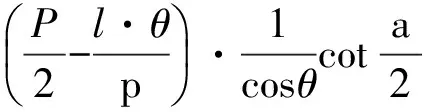
(14)

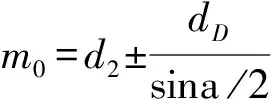
(15)

检验计算的斜置误差按式(8)计算。

必须指出，经过大量计算验证对于对称螺纹上述公式是正确的，但对于锯齿螺纹，只有在螺旋升角较小时实用，否则误差大，不实用，这是因为两牙侧的辅助角应有两个，而不是一个。

1.3　小结

由于公式中包含根式因此Berndt公式受式(4)限制，不满足式(4)Berndt公式不成立；迭代式(2)应该用式(5)代替；初始值式(3)可用θ1=0代替，然后仅用式(5)迭代即可；对于非对称螺纹(如锯齿螺纹)因式(1)中只有一个辅助角θ，由大量的计算表明，螺纹的螺旋升角较大时所计算的中径有显著误差。然而，一般情况下Berndt公式(1)和(5)适用于对称螺纹和螺旋升角不大的不对称螺纹的测试计算，经改造后也可用于所述螺纹的检验计算。

2　苏宗康计算公式讨论

苏宗康先生的计算公式[2]对国内有相当大的影响，探讨如下：

2.1　苏宗康计算公式

在给定实测值m情况下用下式计算被测外螺纹中径d2

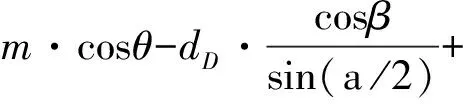
(16)

式中， θ为量球与牙侧面切点和螺纹轴线所构成平面(θ平面)，与量球球心和螺纹轴线所构成平面之间的夹角；β为量球中心与切点的连线与θ平面的夹角；a 为被测对称螺纹牙型角，其半角为a /2；Ph为导程，Ph=nP。

θ和β用下面两式迭代计算

(17)

(18)

切点圆直径dT为

(19)

非对称圆柱外螺纹单一中径按下式计算

(20)

式中， a1、a2分别为左右牙侧角； d21、d22分别为用左、右牙侧角为半角时所计算的中径。

左右两牙侧切点圆直径

dT1=Ph/p ·cosa1·cotβ1

(21)

dT2=Ph/p ·cosa2·cotβ2

(22)

2.2　讨论

2.2.1迭代公式(17)和(18)的讨论

由式(17)可知，若θ=0，则β=0；反之，β=0，θ=0也成立。

从式(18)粗略看，似乎也有式(17)的推论。但该等式右端可化为

(18a)

在θ=0时，由式(18a)得

(18b)

而这与由式(17)当θ=0时则β=0的结果是矛盾的。显然，在θ=0时，式(18)不成立。从几何关系推论，当切点位于量球球心所在轴向平面时，即量针在V型圆环槽中测量跨距情况，θ平面与上述轴向平面重合，于是θ=0，量球球心与切点的连线与θ平面的夹角β=0。因此式(17)是成立的，而θ=0式(18)不成立的推论也就顺理成章了。

然而当用初始值θ=0代入式(18)时β的初始值为式(18b)计算值，从而能用式(17)和式(18)进行迭代计算θ和β。

2.2.2切点圆直径计算式的讨论

将β=0代入式(21)、(22)或(19)，切点圆直径dT1、dT2或dT没有确定值，显然此时这些公式不成立。而从几何关系讲，量针在V型圆环槽中测量跨距时，切点圆直径是确定的。

2.2.3叙述或逻辑不完善

对θ和β含意的说明仅用量球叙述，而外螺纹一般是用量针，没有说明，读者只有用当量量球去理解了，尽管这是牵强的。

2.2.4斜置误差的计算

当θ=0、β=0时，式(16)为

(23)

这是V型圆环槽的计算公式。为了区别，令此时按式(23)的计算值为d20。于是螺纹的斜置误差Δ为

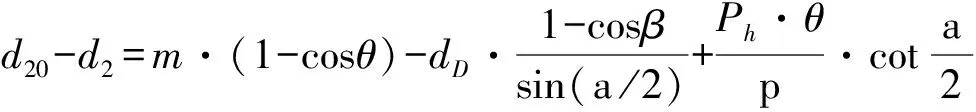
(24)

对于不对称螺纹Δ也套用式(20)计算d2方法求解。

2.2.5检验计算

上述计算是根据已知跨线测量值m计算中径，即测试计算。下面讨论已知中径计算跨线测量值m或M值。

由式(16)可得

(25)

已知中径用式(25)计算跨线测量时量针之间的轴线距离，跨线测量的跨线测量值M为

M=m+dD

(26)

对于V型圆环槽，将θ=0、β=0代入式(25)中得

(27)

斜置误差Δ为

Δ=m-m0

(28)

用式(27)计算值作为初始值，用式(17)、(18)和(25)迭代求解m值，用式(28)求斜置误差。

对于不对称螺纹m0和m也套用式(20)计算d2方法求解，然而对于非对称螺纹并不能确保所得值与用已知m计算d2的结果相同(即用m所得d2反算m结果可能不同)。

2.2.6与Berndt公式的关系

下面讨论式(16)和(17)与Berndt公式的关系。

Berndt公式(1)用本文符号代替，有

(29)

对于对称螺纹a1=a2=a /2，代入上式得

(29a)

由式(17)得

将此式代入式(29a)有

(30)

此式适用于外螺纹和内螺纹，如果只考虑对称外螺纹部分，那么式(30)与式(16)相同。

由式(17)得

将此式代入式(18)有

对此式运算有

(31)

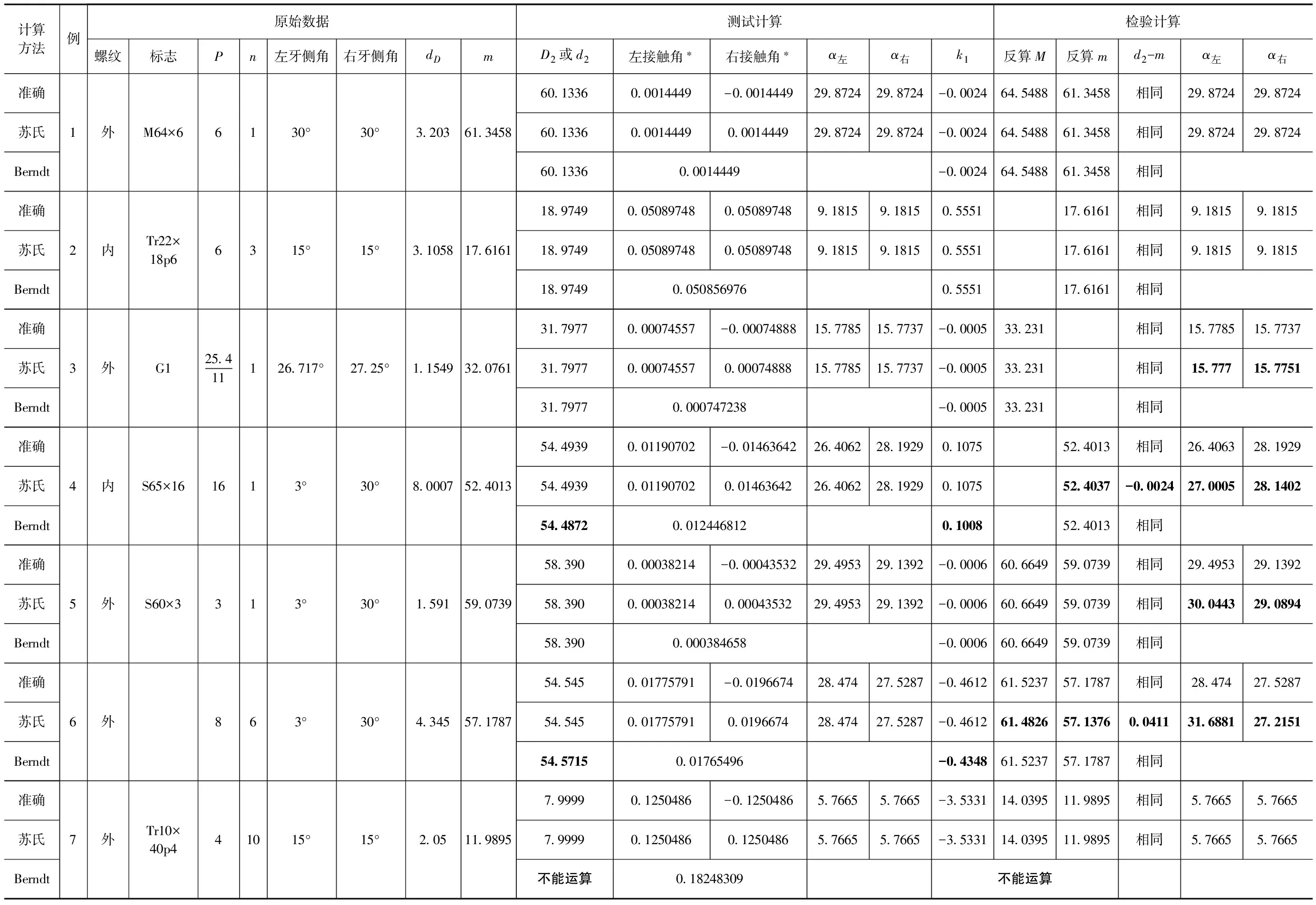
表1　计算示例　单位：mm

*：接触角单位为弧度。

对于对称外螺纹此式与Berndt公式中的迭代公式(2)导出式(11)相同，如果Berndt公式中的迭代公式用sinθ代替arcsin(θk)的话。严格讲与Berndt公式中的迭代公式相当。

由上述证明可知，对于对称外螺纹苏氏公式与Berndt公式相当。对于不对称外螺纹两种公式结果不完全相同，因为苏氏公式要计算两个θ角，而Berndt公式只有一个θ角，这是用Berndt公式可能产生数据误差的原因，参看下文“3 计算示例”的表1。

2.3　小结

这套公式较简单，从大量的计算对比可认为是实用的，尤其是测试计算是准确的，检验计算对于对称螺纹是准确的，不对称螺纹当螺旋升角不大时也可认为是准确的，然而当不对称螺纹螺旋升角较大时有误差。这套公式从数学角度讲并不严谨，甚至有矛盾(如上所述，在θ=0时，式(18)不成立。在β=0时，式(19)也不成立)。

3　计算示例

为了进一步理解前面论述，有必要举出有代表性的计算实例说明。应用文章“螺纹单一中径的三针和量球法测量”[6]所提供的程序“螺纹单一中径的计算”可很方便的进行实例计算，其中作者所述方法在此称为“准确” 方法，另外两种方法用人名称谓。

计算示例

计算示例见表1，表中数据所得值θ角单位为弧度，数值由运行程序源代码时获得，其它所得值由程序可得。

表1中，例1～4原始数据按文献[1]EA-10/10，例5原始数据取自生产数据，例6原始数据取自苏氏文献[2]，例7原始数据取自文献[4]。

例1和例2为对称螺纹，测试计算和检验计算结果三种方法相同。虽然例7也为对称螺纹，测试计算和检验计算结果虽然“准确”和“苏氏”两方法相同，但“Berndt”方法却不能计算，其原因在于不能满足该组公式成立的条件，即式(12)的要求。在此，sinθ=0.18248309>dD/m=0.170983，Berndt公式组不成立，所以不能运算。

例3和例5为非对称螺纹，但螺旋升角较小，三种方法计算结果基本相同，只是“苏氏”方法检验计算的接触半径有差异。

例4和例6螺纹的螺旋升角较大，“Berndt”法的测试计算中径与另两种方法结果有差异，其原因在于这种方法只有一个辅助角的缘故。但是，用这个有差异的中径去进行检验计算可以获得原来的m值，即检验计算结果是一致的。“苏氏”方法虽然测试计算结果是正确的，但检验计算结果有误差。

小结

由表1计算示例可知：

1)“准确”法对测试计算和检验计算都是准确的。

2.)“苏氏”方法对测试计算是准确的，检验计算对称螺纹是正确的，对非对称螺纹会有误差。

3) “Berndt”法在其公式组成立的条件下，测试计算对称螺纹是正确的，对非对称螺纹且螺旋升角较大时计算的中径有误差，检验计算是正确的，但当公式组不成立时不能进行计算，而上述两法没有这种限制。

4　结论

文献[6]不仅给出理论推导严谨且简单的公式且与V型圆环槽测量的公式有机地联系，并证明后者是前者的特例，又由计算示例证明该组公式对测试计算和检验计算都是准确的。

对欧盟和世界有重大影响的Berndt计算公式进行了讨论，得出了该公式组成立的条件，确切了其迭代公式的含意和改善了迭代应用，通过计算示例指出了当公式组不成立时不能进行计算并证实Berndt计算公式测试计算对称螺纹是正确的，给出了对非对称螺纹且螺旋升角较大时计算的中径有误差的评价。经改造后也可进行检验计算。

苏氏计算公式对国内有相当影响，通过讨论 可知该公式组虽然理论上欠严谨，但公式较简单，且由表1计算实例证明它对测试计算是准确的，检验计算对称螺纹也是正确的，对非对称螺纹可能有误差。

[1]EA Guidelines on the Determination of Pitch Diameter of Parallel Thread Gauges by Mechanical Probing EA-10/10，P10，P20

[2]苏宗康. 非对称阿基米德螺纹的精密测量, 计量技术,1995(2):6-9

[3]苏宗康. 非对称螺纹精密测量的误差研究，实用测试技术,1999(6):29-31

[4]徐孝恩.螺纹检验与测量.北京:计量出版社，1984:148-149

[5]刘远模.量针测量螺纹斜置误差的公式讨论.计量技术,2009(2):55-57

[6]刘远模.螺纹单一中径的三针和量球法测量.计量技术,2014(1)