永磁体磁偏角测量方法的研究*
2014-03-22侯瑞芬张志高王京平林安利
侯瑞芬 张志高 范 雯 贺 建 王京平 林安利
(中国计量科学研究院,北京 100013)
0 引言
永磁体磁偏角指永磁体的最终磁化矢量方向的偏角。永磁体在磁取向成型的过程中,产品取向方向和取向磁场方向不平行而产生磁偏角,或者在产品交工过程中,装夹产品时未找正而使产品几何对称轴与产品磁轴间产生磁偏角。磁偏角的存在,使磁体非磁化方向产生磁场,形成杂散磁场。随着永磁体应用的不断深入,磁偏角成为精密磁性器件性能的重要影响因素。比如在精密磁悬浮器件中,如果磁体存在一个较大的磁偏角,则磁悬浮轴承的转子和定子悬浮时也会有一个相同量级的偏差角度,此偏差角度的存在将极大影响磁悬浮的性能,甚至导致磁悬浮轴承不能正常稳定悬浮,磁偏角的存在将造成系统不对称、偏心、动力学性能差等不利影响。另外,在电机的应用方面,较大的磁偏角不仅使永磁体的磁性能得不到充分的利用,而且会使电机的性能恶化。因此,磁偏角已经成为衡量永磁性能的重要指标,磁偏角的测量越来越受到重视。
本文针对国内永磁材料企业的测量需求,提出了一种基于亥姆霍兹线圈的旋转磁体的磁偏角测量方法,同时建立了相应的测量装置。该方法经济实用,适用于多种形状永磁体的成品检测,因此,根据该方法研制的磁偏角测量仪在国内企业得到了广泛应用。
1 测量原理和数学模型的建立
本文提出的测量方法基于亥姆霍兹线圈与磁通计组合形成的开磁路磁矩测量原理,这是目前开路成品磁体磁矩检验最方便、最准确的方法之一。如图1,M′为理想磁化方向的磁矩,M为实际磁化方向的磁矩。在理想磁化方向下,该方法测量的是磁体磁化方向的总磁矩,这时M′=M。但是,当实际磁化方向与理想磁化方向有偏差时,磁矩测量结果为实际磁化方向在理想磁化方向的磁矩分量,这时M′=Mcos(g )。按照这一原理,通过测量不同的磁矩分量即可得到磁偏角g 的值。为了便于分析,采用图2所示的三维磁体磁化方向矢量图建立数学模型。

图1 实际磁化方向

图2 磁体磁化方向矢量图
图2中,F为被测样品磁化方向的磁矩值;z为几何对称轴,也就是理想的充磁方向;按照磁偏角的定义,g 为最终需要测定的磁偏角;W1、W2和W3分别为F在zoy、xoy和xoz的投影;Fx、Fy、Fz分为F在x、y和z轴的分量。按照图2的矢量关系,可得到以下公式:
(1)
(2)
(3)
由式(1)~式(3)可得:
(4)
在实际生产过程中,磁偏角g 是一个很小的值,通常在5°以内,因此,在xoy平面内的投影W2相对于W1和W3是一个很小的值,而且W1与W3近似相等,式(4)可以简化为:
tang =W2/W1或tang =W2/W3
(5)
从而得到二维测量的简化式:
g =arctan(W2/W1)或g =arctan(W2/W3)
(6)
由于磁矩值与磁通的大小成正比,因此,实际测量中直接测量磁通值就可以了。
2 测量装置的建立
2.1 装置的构成
基于以上数学模型设计的测量装置如图3所示,主要包括计算机、磁通计、线圈、样品台和电机。样品台与电机相连,上电后电机可驱动样品台旋转。测量时,样品放到工作台上,保证样品置于线圈的均匀区中,电机通过样品台带动被测样品在线圈中旋转运动,根据电磁感应定律,此时,线圈将产生感应电压输入到磁通计,磁通计就可实时记录磁通量的变化,并通过RS232接口将数据发送到计算机,计算机通过对一个周期内的数据处理,可得到相应放置方向的磁通。改变样品的放置方向,用同样的测量方法可得三个不同方向的磁通分量,最后,按照式(4)计算得到磁偏角g 。在实际测量过程中,为了提高检测效率,可以按照式(6)的方式,只测量两个方向的磁通即可得到永磁体的磁偏角。

图3 测量装置示意图
2.2 测量装置的研制
数字磁通计采用RC模拟电子积分器和基于32位ARM单片机控制的数字电路组成,数字电路完善了传统RC积分器的功能,实现了磁通计的智能化。一方面具有RS232串行口,可与计算机通讯,为该测量方法的实现奠定了基础;另一方面,采用DA自动跟踪反馈到输入端的方式实现了磁通计飘移的自动调整,保证了测量的准确性和自动化。
测量装置中的亥姆霍兹线圈和样品台是非常重要的两个部分,亥姆霍兹线圈的大小和绕组需要与被测样品的尺寸以及磁通计的量程相匹配。在机械加工和安装方面,亥姆霍兹线圈要保证垂直度,样品台需要保证足够的水平度,否则,这两方面将直接影响测量的准确度,为此,专门设计了调节机构和校准办法来保证安装精度。
数字磁通计通过RS232串口与计算机通讯,计算机记录电机旋转一周期内的数据同时绘制曲线,一周期测量结束后,将最大值和最小值相减计算出对应方向的磁通值,这种计算方式有效的消除了积分器飘移对测量结果的影响。
3 装置的校准
按照以上方式建立的测量装置,亥姆霍兹线圈的安装垂直度和样品台的水平度将直接影测量结果,因此,设计了一套校准办法,以减小加工和安装引入的测量误差,进一步提高测量的不确定度。
图4中,左侧为校准用的无磁立方体,按照加工要求,该立方体各个面的垂直度可以达到90°±0.05°。校准时, 将被测样品分别放置在立方体的A、B、C三个面上,同时保证理想磁化方向与线圈中心轴平行,旋转测量三个方向的磁通值,然后,按照式(4)计算磁偏角。在理想情况下,计算结果应该是45°,如果考虑校准用立方体的加工误差,三次测量由校准立方体引入的测量不确定度小于0.15°,如果计算结果大于0.15°,就说明样品台或者线圈的安装带入了测量误差,根据测量结果对线圈的中心轴方向进行调整,从而将由设备引入的测量不确定度控制在0.20°范围内。

图4 校准示意图
4 试验结果
为了验证本文提出的测量方法,表1给出一个钕铁硼样品的测量结果。从测量结果可知,该方法的测量重复性小于0.20°,比较三维算法和二维算法可知,采用简化后的二维算法,测量结果接近三维算法,因此,在实际测量中,完全可以用二维测量方法代替三维。
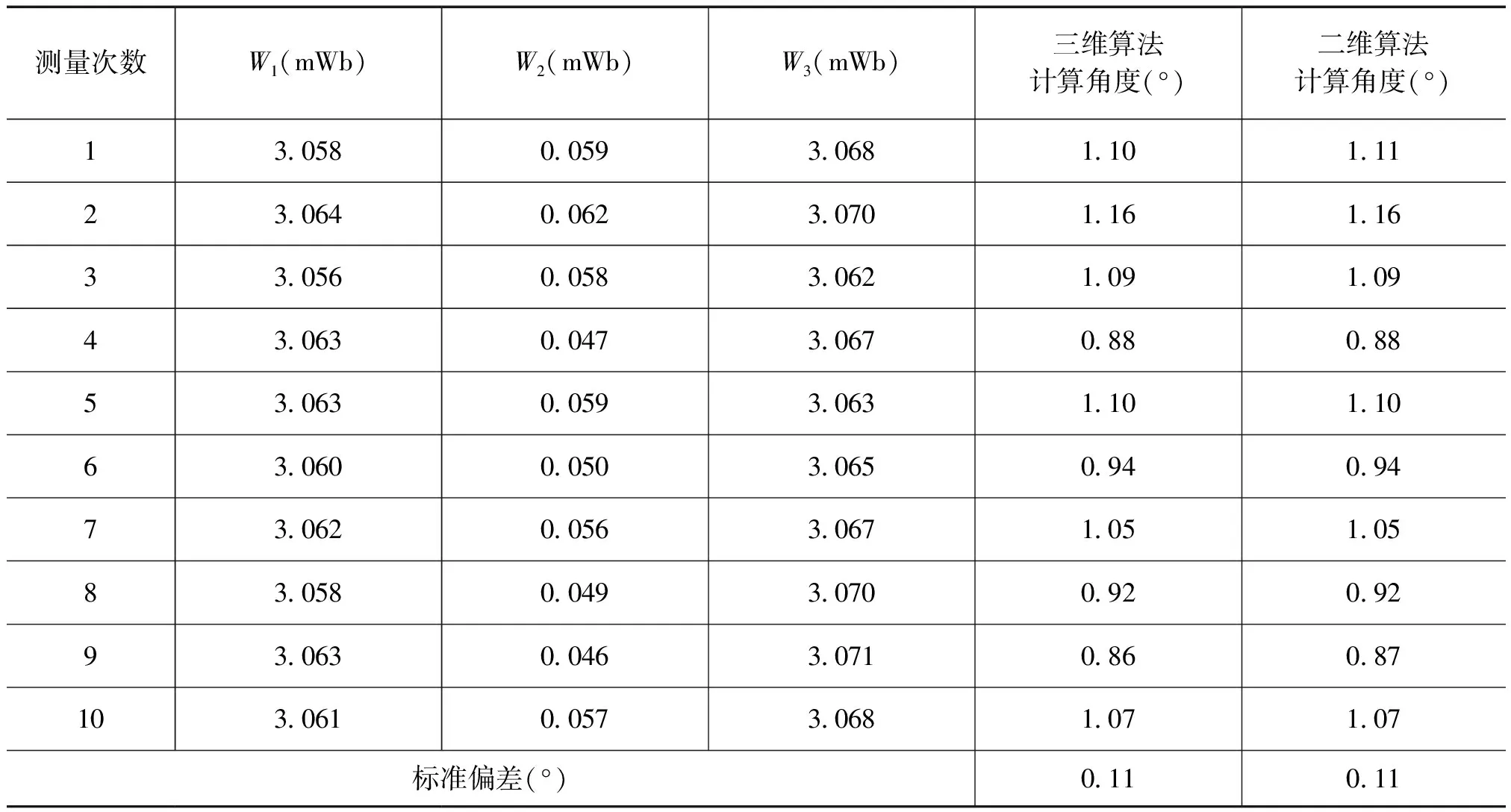
表1 10次测量结果
5 结论
本文从磁矩测量原理出发,提出了永磁体磁偏角测量方法,并且研究了相应的测量设备和校准办法,实现了永磁体磁偏角的准确测量。校准过程和实验结果表明,测量设备的最大允许误差0.20°,测量重复性优于0.20°,可以满足永磁体磁偏角的测量需求。根据数学模型和试验结果,进一步提出了简化的二维测量方法,满足了生产中永磁体磁偏角测量的需求。
[1]周寿增,等.烧结钕铁硼稀土永磁材料与技术. 冶金工业出版社,2011
[2]林安利,等. 中国电气工程大典(第一版).北京:中国电力出版社,2009
[3]方凯,等.永磁体磁化方向偏差的研究.上海电气技术,2008(9)
[4]李冶夫. 永磁体磁化矢量方向偏角检测与控制. 北京:中国科学院研究生院,2010
[5]倪育才,等.实用测量不确定度评定.北京:中国计量出版社,2008
