热管蒸发段与冷凝段长度比的最佳值

范　砧　范京溟　陈建军

(华油华锐节能环保设备有限公司 ，任丘 062552)

0　引言

在设计热管换热器时，必须确定热管蒸发段与冷凝段长度比例的最佳值。我们知道，在同样大小的温差下，传热热阻越小传热量越大。单根热管的总传热热阻是由若干热阻构成的，它又是蒸发段与冷凝段长度比的函数，故须求得总热阻函数曲线的最小值时的长度比。从而得到最佳长度比，以使热管的总热阻最小。

1　探讨的出发点

由参考文献[1]我们知道了单根热管热阻的构成，并把它作为我们探讨的出发点。热管的热阻如图1所示。单根热管的这7个热阻是串联的。各热阻的意义如表1所示。设总热阻为R[℃/W]，则：

图1　热管的热阻

式中：L为热管各区段的长度，m；do为管壳外径，m；di为管壳内径，m；rF为污垢系数，m2·℃/W；a为单位长度热管含翅片的外表面积，m2/m；η为热管的肋壁效率；P为管材导热系数,W/(m·℃)。

实验证明其余3个热阻均很小，为简便，在此可忽略之。

表1　热管的热阻

1　最佳值的导出

(1)

式中：下标c、e分别表示冷凝段和蒸发段。

代入式(1),并认为左边等于右边,于是有：

(2)

我们已经把单根热管的总传热热阻R表示成了蒸发段与冷凝段长度比x的函数。为了认识这个函数，先由感性入手，再进行理性推演。

例1.我们在设计某台热管换热器时的数据为：do=0.032m，di=0.026m，LL=2.980m，ae=0.2884m2/m，ac=0.7875m2/m，ae=50.25W/(m2·℃)，ac=26.06W/(m2·℃)，ηe=0.8759，ηc=0.9049，pe=53.25W/(m·℃)，pc=56.20W/(m·℃)，rFc=0.0004m2·℃/W，rFe=0.0002m2·℃/W。代入式(2)，整理后得：

R=0.01846(x+1)+0.02691(1+1/x)

=0.04537+0.01846x+0.02691/x

绘制R～x曲线如图2所示。

图2　热管热阻与长度比的变化曲线

由图2.可以看出：这条曲线是凹形的，做水平切线MN，得切点(12，89.95)。实际上，就是当x取1.2时，R有最小值0.08995(m2·℃/W)。

(3)

令

则

(4)

因为do/di>1,ln(do/di)>0 (e=2.7183), 又因为2ppe·LL>0,所以C>0,又证得D>0。在x永为正值的情形下，有：

因为x的负值不存在，所以：

(5)

这个驻点就是热管蒸发段与冷凝段长度比的最佳值。

2　最佳值的一般计算式

由上面的推演，我们知道式(5)适合冷凝段绕有翅片而蒸发段也绕有翅片的热管。但在实践中，也有冷凝段绕有翅片而蒸发段是光管的及两段皆为光管等情形。在计算最佳值时，它们的区别仅在单位长度面积和肋壁效率上。

对于光管，不论在蒸发段还是冷凝段，都有：

aeηe=pdo，acηc=pdo

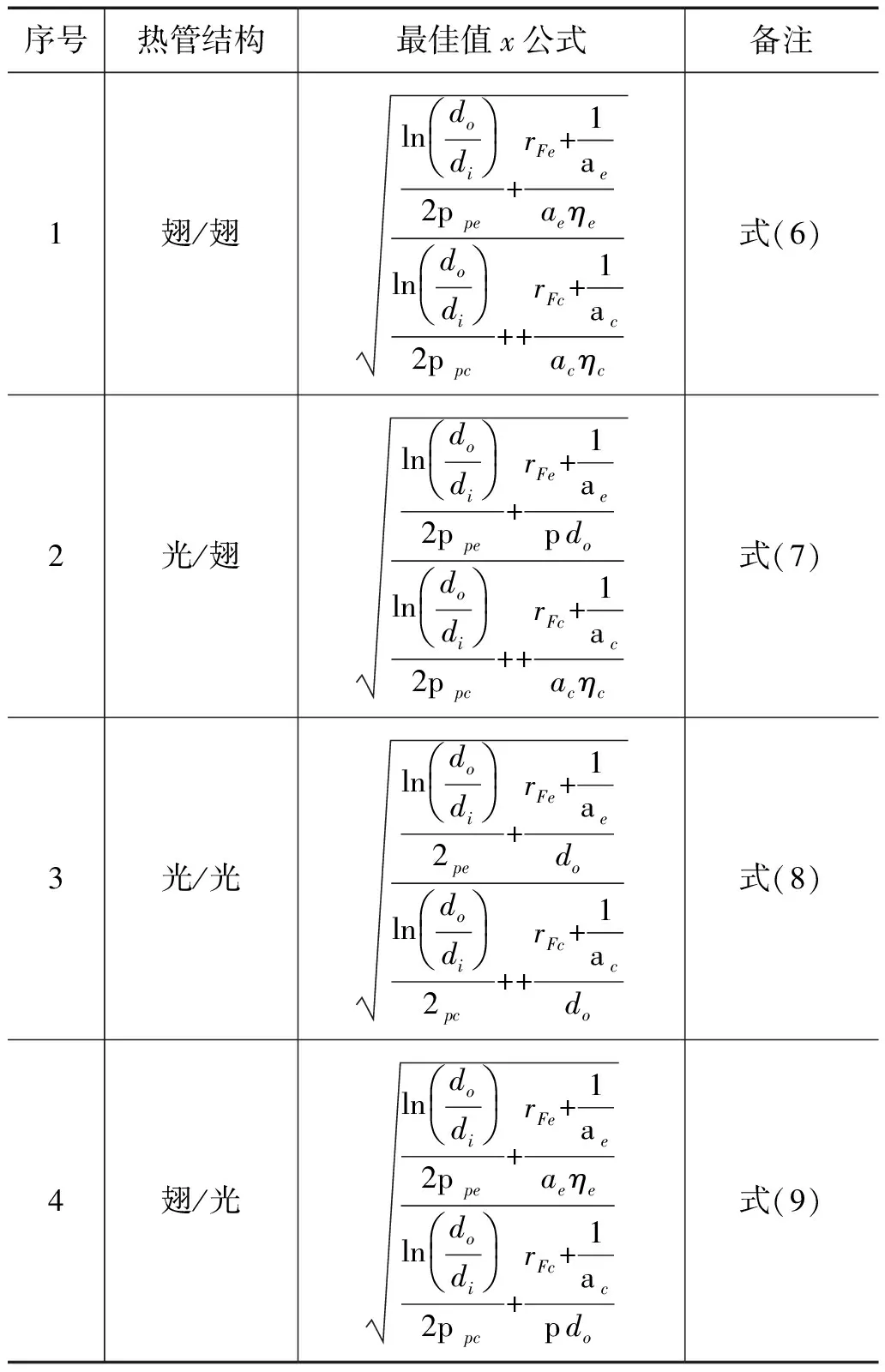
表2　热管四种外壁结构的最佳值

按“蒸发段/冷凝段”有无翅片的4种结构：“翅/翅”、“光/翅”、“光/光”和“翅/光”，分别把上式代入式(5)，整理后得到在设计热管时可以编入计算程序的实用公式，如表2所示。

3　结束语

依据用户的已知条件，选择表2中一种最佳值的实用计算公式。在一般情况下，最佳值不是一下子就能找到的。先设试算长度比xs，由所选择的实用计算公式算得的最佳值为x, 定义长度比的相对偏差W：

(10)

例2：把例1的已知数据代入式(6)，并设Le=1.625m,Lc=1.355m, 算得：

xs=1.1993

x=1.2075

W=-0.68%

此值与例1的结果是惊人的一致，从而也说明了式(6)的正确性。

如果在某次设计中,W为(-0.5%～-1.5%),那么就可以把这次算得的x值确认为长度比的最佳值。经验证明,这是合理的,因为冷凝端常有不凝性气体聚积,形成气塞,必然缩小了冷凝段的有效长度。对碳钢-水热管最为明显,因为它有氢气产生。W=0的x理想值,不适合有不凝性气体聚积的实际情况。

[1]钱滨江，等.简明传热手册[M].北京：高等教育出版社, 1983

[2]庄骏，等.热管技术及其工程应用[M].北京：化学工业出版社,2000

[3]樊映川，等.高等数学讲义.北京：人民教育出版社, 1962

[4]范砧.热管等温性测量及其准确度的评定.计量技术，1992(3)

[5]范砧，等.等精度直接测量列数据处理方法的完善.计量技术，1990(9)