基于计算几何和遗传算法的直线度误差评定*

李　彬　赵惠英　赵则祥　席建普　任东旭

(1.西安交通大学， 西安 710049；2.中原工学院，郑州 450007)

0　引言

随着现代计算机计算速度的提高和计算几何算法的成熟，计算几何算法在形状误差的评定中已经得到广泛的应用和研究。形状误差虽然被划分为低频误差，但在对其进行评定时，公称尺寸均被引入到评定计算中，因此具体的评定实际转化为一个尺寸计算问题。形状误差的评定原来均是采用优化算法进行处理，如最小二乘法、最速下降法和遗传算法等[1-3]。

对于最小区域法直线度误差的评定，国内外已进行了广泛地研究，除了直接用优化方法评定外，计算几何[4]评定方法在采样点数较少时亦常被采用，拟合凸多边形法即是这类方法之一。要使用该方法来评定最小区域直线度，首先要根据(平面内的)被测点建立其相应的凸多边形。建立平面内一组点的凸多边形是计算几何中一个关键问题。

1　最小区域直线度误差定义

平面内直线度公差的定义为：在给定平面内，公差带是距离为公差值t的两平行直线之间的区域。评定时首先用两条平行直线包容被测实际要素，当其中一条直线至少有两点与被测实际要素接触，另一条平行直线至少有一点与被测实际直线接触且该接触点位于上述两接触点之间，则由上述两平行直线形成的区域即为最小包容区域。

对于平面内被测量的一组数据，首先建立起它的平面坐标系，其坐标表达式为(Xi，Yi)，i=1，…，n，然后根据这些测量点拟合出参考直线，参考直线的方程表达式为

Y(X)=aX+b

(1)

式中，a为参考中线的斜率；b为参考中线的截距。

则最小区域直线度误差的优化函数定义为：

(2)

式(2)中，m为采样点数；

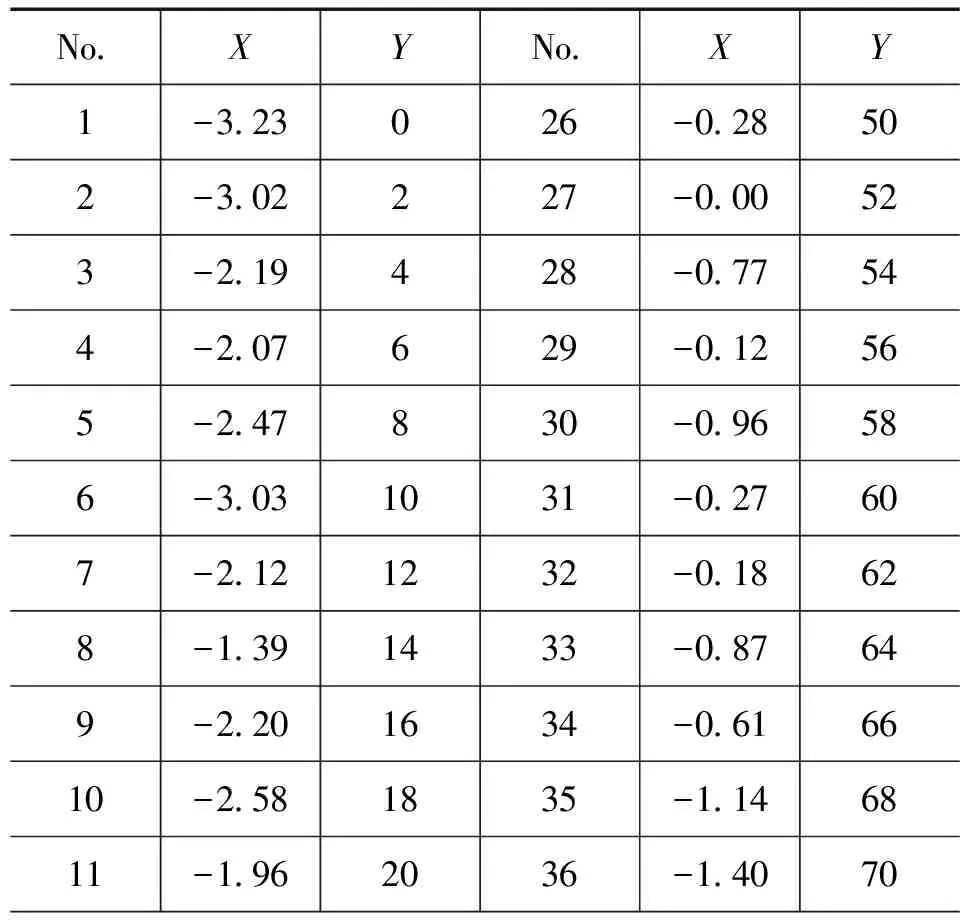
表1　素线直线度的测量数据X：μm，Y：mm

续表

2　最小区域直线度的计算几何算法评定[4]

为说明计算算法的实施步骤，采用表1所示的直线度测量数据。该算法的步骤如下：

1)根据被测点的X(测量长度)坐标(Z向位移)进行排序；

2)连接首尾两点得到一条中线，以该中线为界将被测点划分到两个区域中，如图1所示；

3)将两个区域分别为‘上区’和‘下区’，若点在中线下方，则点归类为下区；反之，则归类为上区，如图1所示。据此所有被测点被划分成了上下两组数据；

点的划分方法如下：首先连接首尾两点，得到中线Lm，其方程式为：

Y=ax+b

(3)

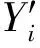
图1　数据分区

图2　上凸多边形

4)被测点的分割完成后，就要分别在上下两区内进行凸多边形拟合了。拟合过程实际上就是保留凸顶点，舍去内点。下面以下区拟合为例进行说明，设其包含n个点，首先连接Pn-1和Pn+1，其连线为Ln，根据Pn与Ln的关系来判断Pn点是否为凸顶点，判断条件为：若Pn在Ln的下方，则为临时凸顶点；若在上方，则其必为内点，可舍弃。所建立的上半凸面如图2所示，进而可以得到下半凸面，如图3所示。

5)得到凸多边形后就可以求解最终的最小区域直线度误差，如图5所示。求解方法为：设所求得的凸多边形的边数m，则其凸顶点的个数为m个。设边Li的直线方程为Y=Ai+BiX，求出各顶点与该边的距离(不包括该边的两个端点)，挑选出最大值，根据式(2)中的判别准则，最小区域直线度误差可以表示为：

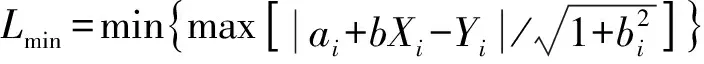
(4)

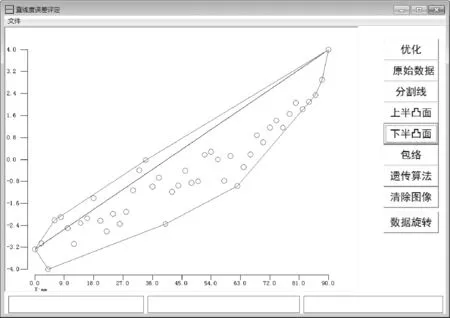
图3　下凸多边形图

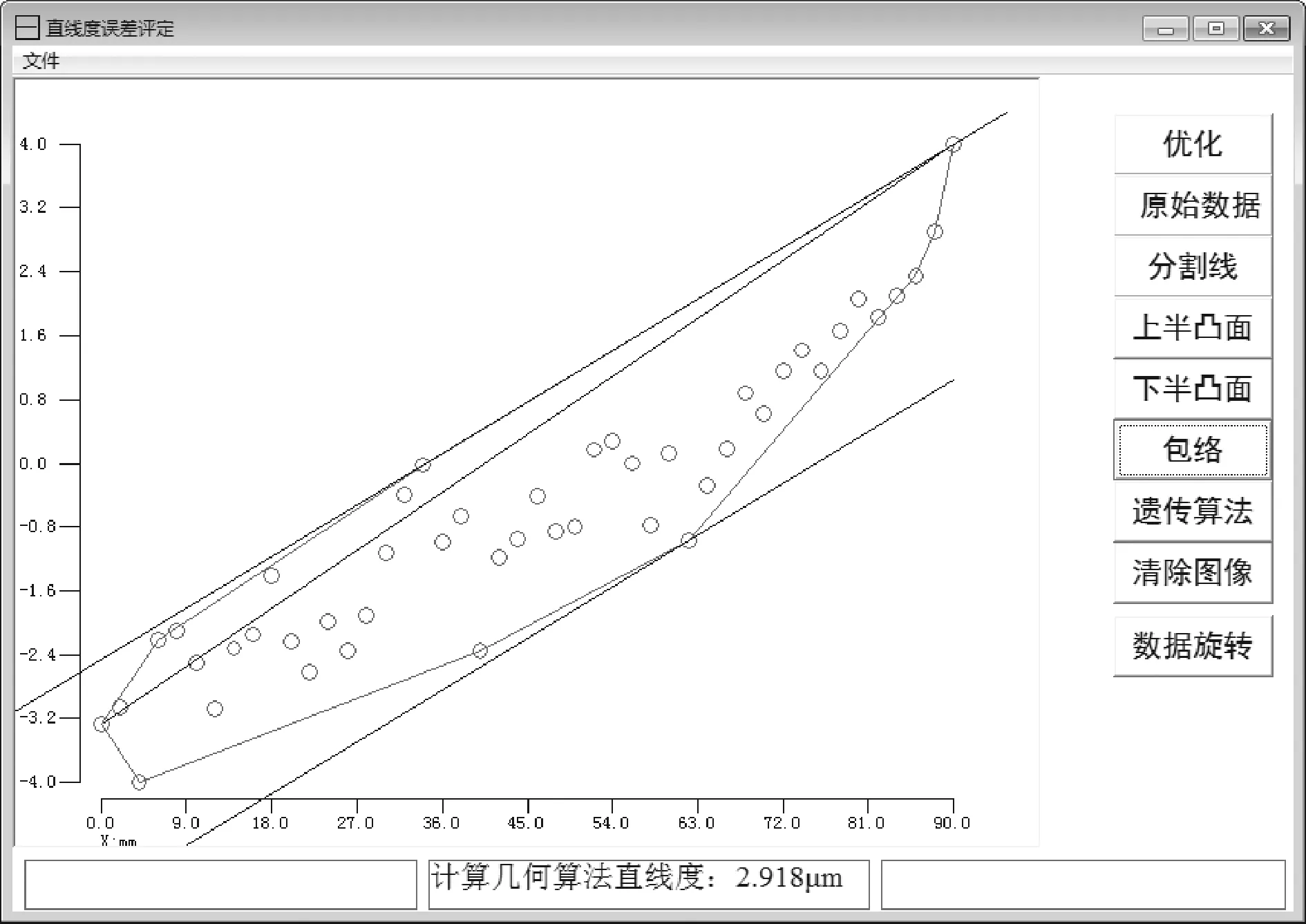
图4　凸多边形及最小区域包络线

算法流程如表2所示。

表2　计算几何算法评定直线度流程

3　最小区域直线度的遗传算法评定

为了验证计算几何算法对最小区域直线度评定的优势，作者使用了遗传算法[5]来进行比较。采用的数据仍然是表1所示的测量数据。

采用的遗传算法如下：

1)首先利用最小二乘法拟合被测数据的参考直线参数a0，b0，所需优化的目标函数为式(2)。

2)由于最优解与最小二乘解的偏差很小，选择解搜索区间为(-a0，-b0)～(2a0，2b0)，以最小二乘解为初始值。

3)考虑到二进制编码、解码操作简单，交叉、变异等遗传操作便于实现，因此选择二进制编码。为保证精度，优化参数的有效数字保留到小数点后14位。由于优化参数的数值较小，分别将此四个量乘以1014，分别用二进制数表示，得到所需要的编码长度分别为nxi，i=1:N。

大量试验表明执行代数m1和群体个数n1可以分别选择为30和50，若选择更大的进化代数和群体个数并不会得到更优解，只会影响效率。

4)生成初始群体。令T=rnd(1)，若T≥0.5，则选择代码1，若T≤0.5，则选择代码0。分别根据编码长度nxi，i=1:N，生成群体个数为50的初始种群。

5)解码计算每个个体的适应度值。将二进制表示的个体转化为十进制数，并分别乘以10-14，代入到式(4)中得到各自的适应度值。

6)各个个体的适应度值进行尺度变换，采用线性变换法。

7)选择操作采用按比例的适应度分配法进行。

8)以0.25的交叉概率进行交叉操作。

9)以0.05的变异率进行变异操作。

10)将此时的个体利用二进制数表示，并重新回到步骤5)开始，繁殖到50代结束。

11)挑选所有个体的适应度最大值及其对应的xi，i=1:N值。适应度最大值即是要求的目标函数的优化值。

4　算法比较结果

4.1　计算几何和遗传算法的计算结果

采用文中所述的两种算法分别对表1所示的直线度测量数据进行了处理，得到了图5所示的两个包络线。以及表3所示的结果比较表。由表3可以看出，遗传算法和计算几何法的评定结果非常相近。

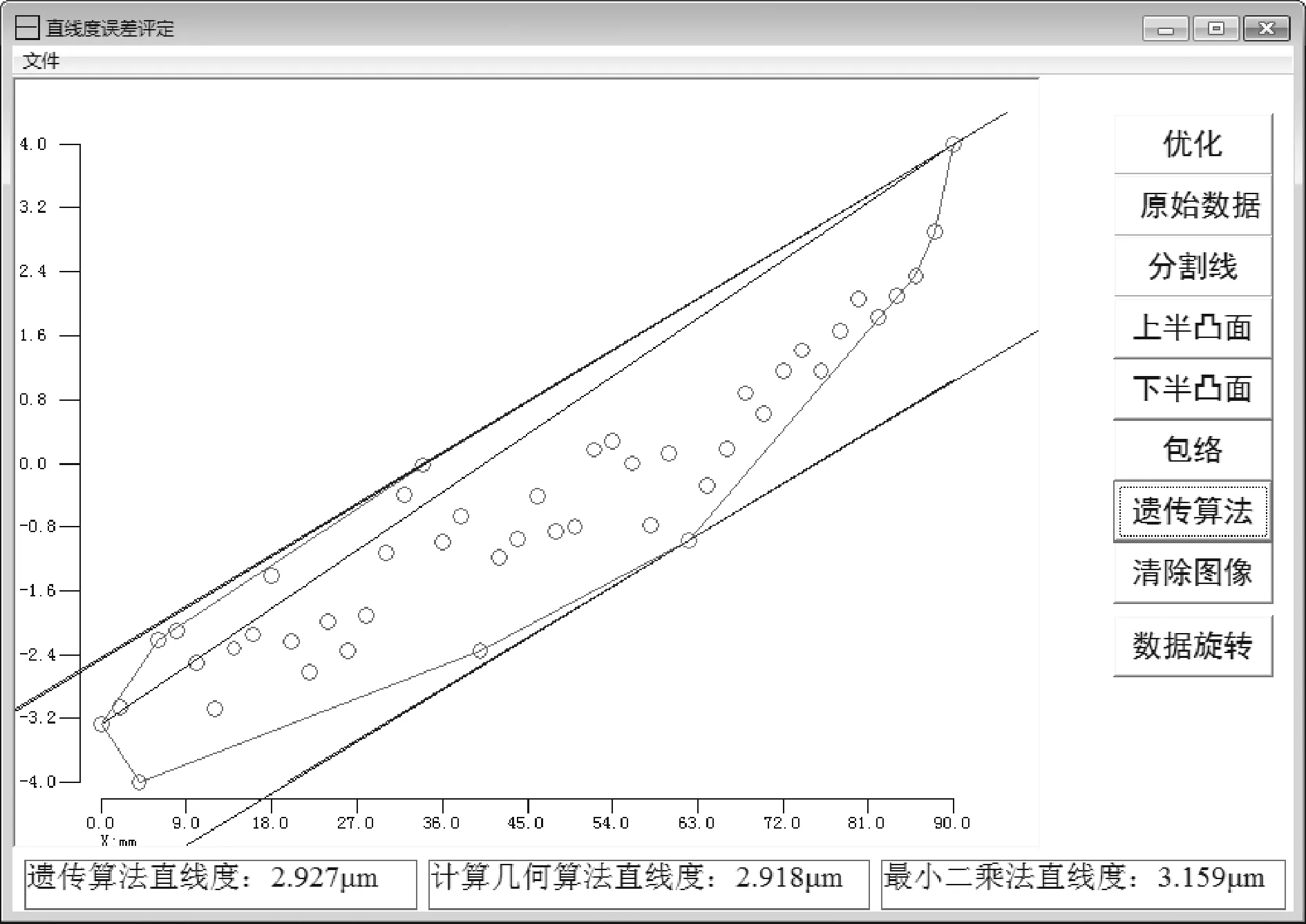
图5　计算几何算法和遗传算法的直线度误差

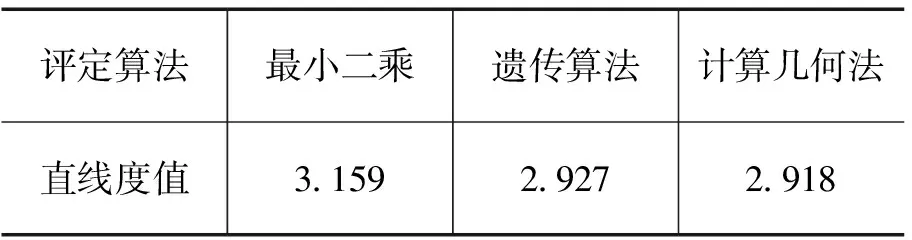
表3　三种素线直线度误差比较表　(单位：μm)

4.2　计算几何和遗传算法的计算结果和效率比较

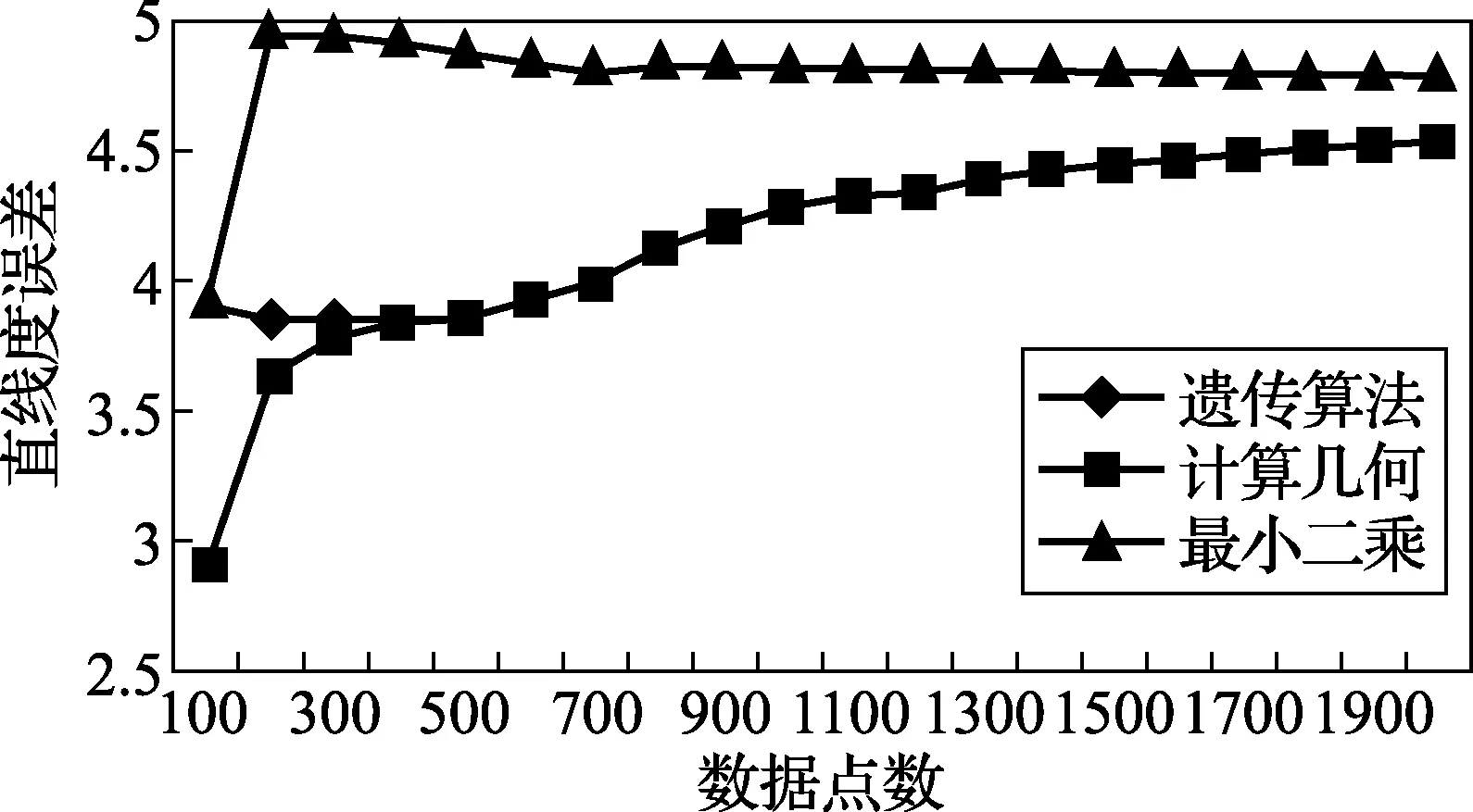
图6　三种算法的计算结果比较

为了比较两种算法的计算结果和效率，采用了20组数据进行比较，20组数据的点数从100到2000，计算结果和效率比较见图6和图7。图6还包含了最小二乘法的计算结果。由图7可以看出，计算几何算和遗传算法的计算结果相近；另随着测量数据的增加，三种算法的计算结果更加接近，这说明随着提取要素数量的增加，测量结果将更趋近于被测要素的实际情况。由图7可以看出，遗传算法的计算效率随采样数量的增加而降低，而计算几何算法的变化较小，即使测量点达到2000点，计算时间仍然小于1s。

5　结论

本文建立了基于计算几何的最小区域直线度评定算法，编写了相应的VB评定和图形显示模块，并将该算法与遗传算法的计算结果及计算效率进行了对比，比较结果和图形显示表明，两种算法的结果相近，但计算几何算法效率更高。

[1]罗英俊，李彬.最小区域平面度的计算几何评定算法研究，制造技术与机床，2009(1)：92-94

[2]Jyunping Huang.An efficient approach for solving the straightness and flatness problems at large number of data points[J].computer-aided design，35(2003):15-25

[3]康敏.求解“最小条件”直线度误差值的精确算法，计量技术，1992(02)

[4]Mark de berg.Computational geometry algorithm and application.London: Springer-Verlag london Limited，1997

[5]王小平.遗传算法:理论应用与软件实现,西安交通大学出版社,2007