一类非线性时滞积分不等式中未知函数的估计

覃永昼

(1.桂林电子科技大学数学与计算科学学院，广西桂林541004;2.河池学院数学与统计学院，广西宜州546300)

0 引言

众所周知，研究非线性微分方程的重要工具之一是Gronwall-Bellman型积分不等式［1-2］.最基本的Gronwall-Bellman型积分不等式是指:如果c≥0是常数，u和f是区间［a，b］上的非负连续函数，满足积分不等式

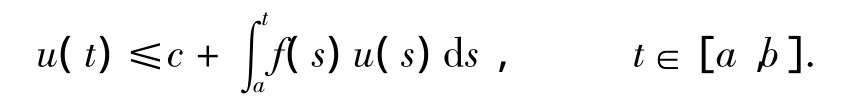
则

Bihari［3］对下面的积分不等式作出了重要贡献:

其中a＞0是一个常数。

文献［4］研究了时滞线性积分不等式

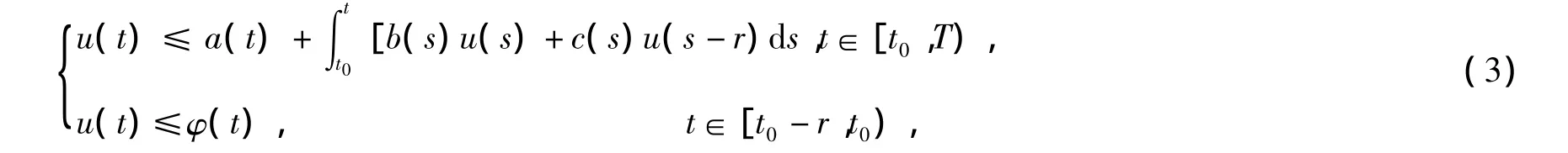
和弱奇异线性时滞积分不等式

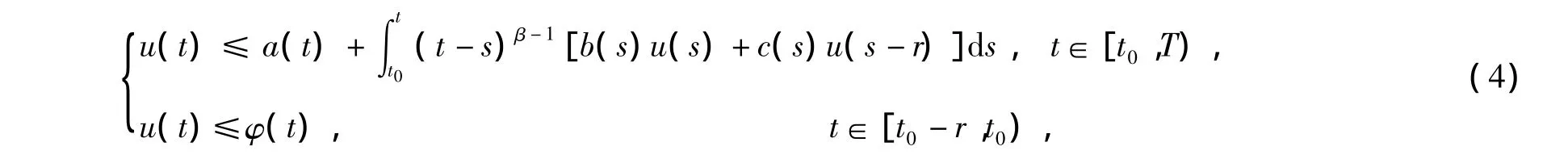
本文受文献［4］与文献［5］的启发，研究下面的非线性弱奇异时滞积分不等式

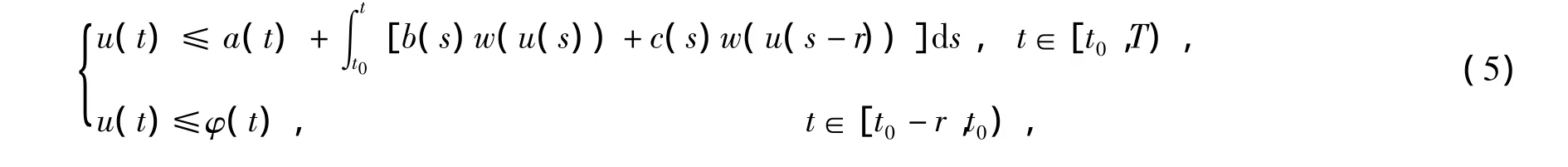
和

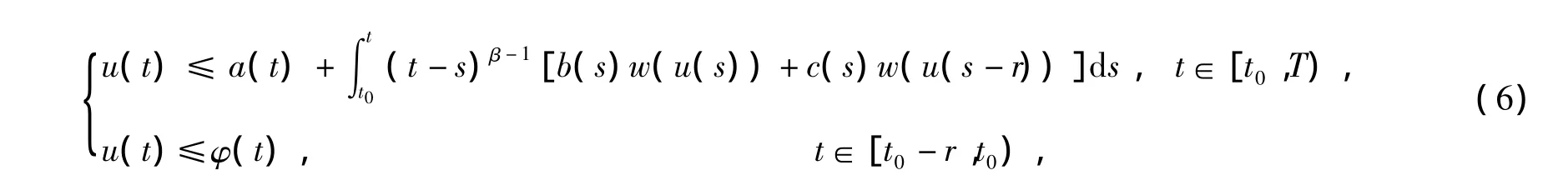
1 主要结论

在本文中， RR+=［0，+∞).

为了叙述方便，我们在给出主要研究结果之前先介绍几个引理和定义。

定义1［5］:我们说函数w: RR+→ RR满足条件(q)，如果

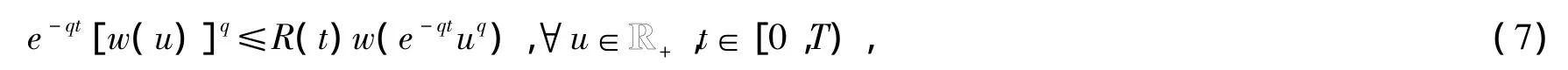
成立，其中R(t)是连续的非负函数，q和T是两个正常数。

引理1［5］:(1)若β＞1/2，则有

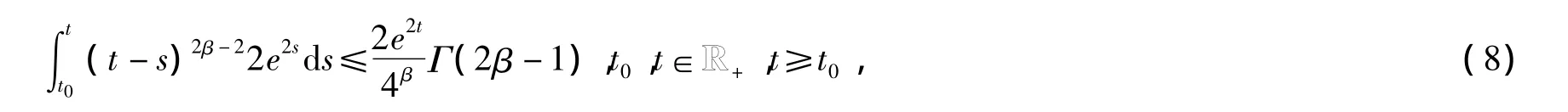
(2)若β∈(0，1/2)，p=1+β，则有

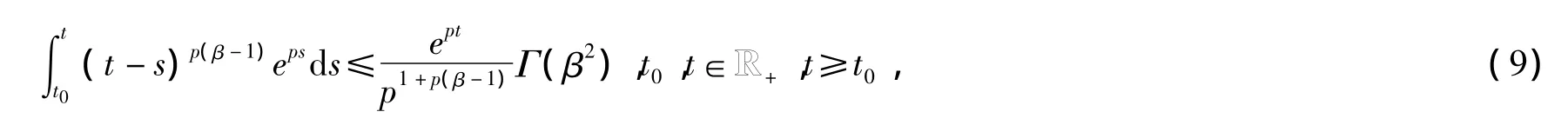
引理2［6］(离散Jensen不等式):假设A1，A2，…，An是非负实数，r是大于1的实数，n是自然数，则有不等式成立。

引理3［7-8］(比较原理):假设w(t，x)是区域Ω:={(t，x):t，x∈ RR+}上的连续的实值函数，u(t)是 RR+上的可微函数。如果函数u(t)满足不等式

又假设x(t)是微分方程

的最大解，而且有u(0)≤x(0).则有

现在给出我们的主要结果与证明。

定理1:假设a，b，c，u，φ是定义在区间［t0-r，T)上的连续非负函数，t0，r，T是正常数，函数w是定义在非负实数集 RR+上的非负函数，w满足下列条件:

(1)次可加性，即对于任意t，s∈ RR+，不等式w(t+s)≤w(t)+w(s)成立;

(2)对于任意t∈［t0-r，T)，不等式w(t)≤Lt成立，L是正常数;

如果函数u满足不等式(5)，则对任意t∈［t0，t0+r)有

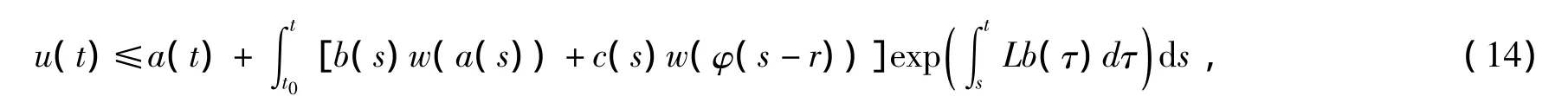
对任意t∈［t0+r，T)有

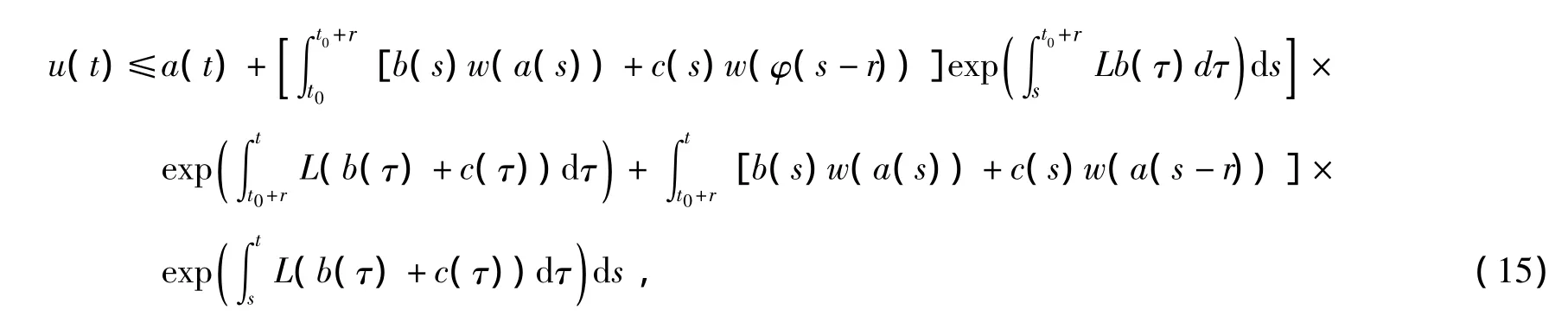
证明:定义函数z(t)如下

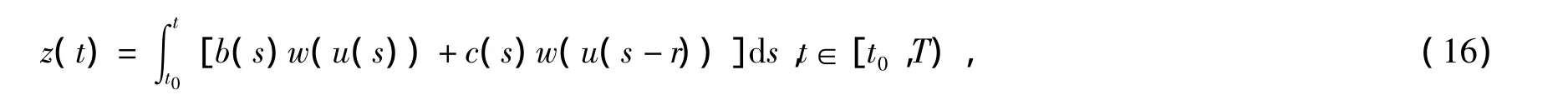
那么z(t0)=0，u(t)≤a(t)+z(t)，z(t)是非负、非减单调函数，且有

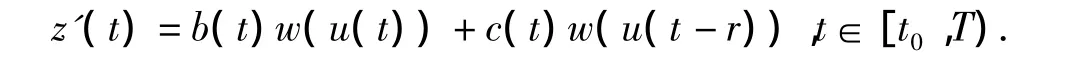
如果t∈［t0，t0+r)那么由w满足的条件，可以推出

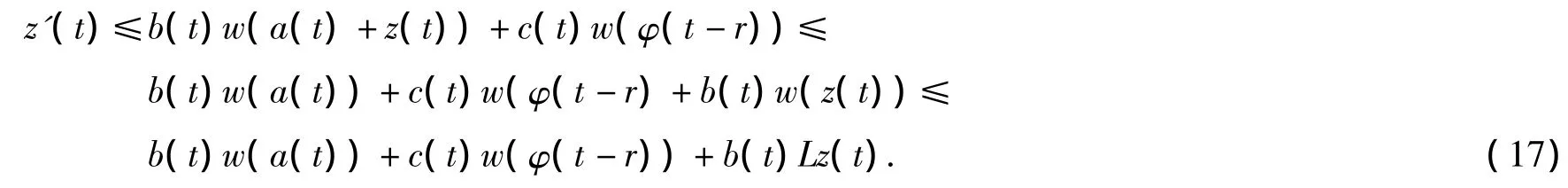
另一方面，根据微分方程的常数变易公式知道下面微分方程

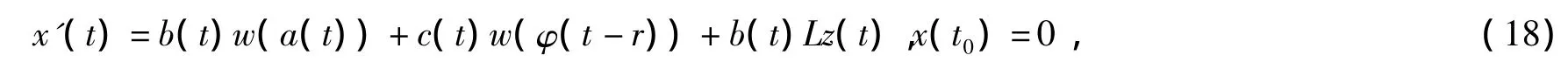
的解为

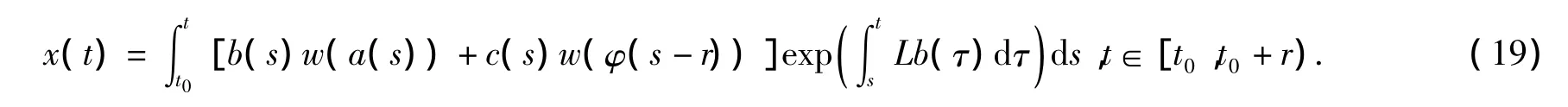
根据比较原理，即引理3，由式(17)我们可以推出

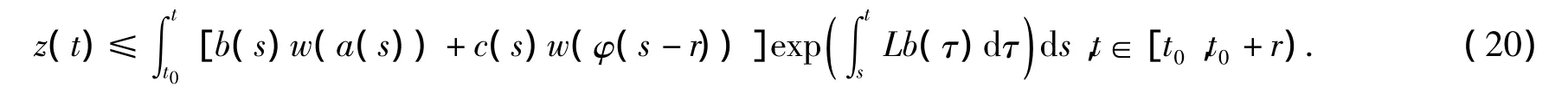
如果t∈［t0+r，T)，那么由w满足的条件，可以推出

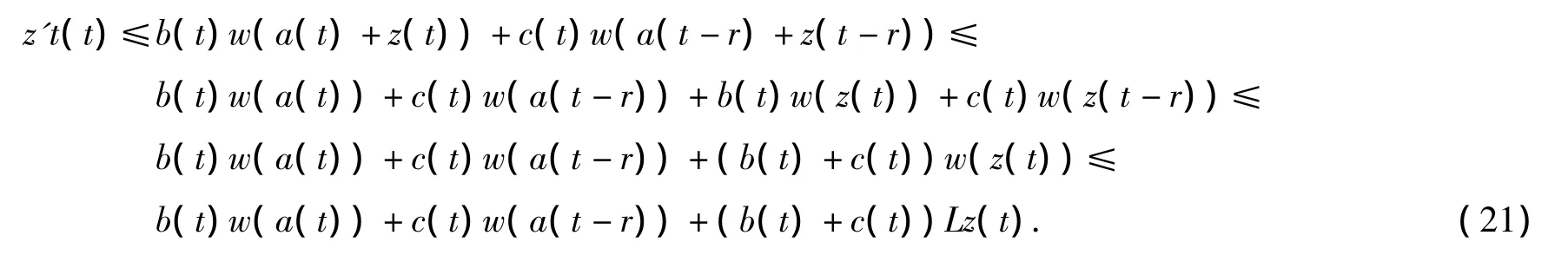
再次利用微分方程的常数变易公式和比较原理，由式(21)我们可以推出对任意t∈［t0+r，T)有

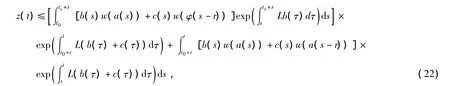
利用关系式u(t)≤a(t)+z(t)，由式(20)和式(22)得到我们要证明的结果式(14)和式(15)。

定理2:假设a，b，c，u，w，φ，r满足定理1的条件，β是正常数，w还满足(q)条件，即满足不等式(7)。如果函数u满足不等式(6)，则有下列估计式:

(1)当β＞1/2时，对任意t∈［t0，t0+r)有估计式

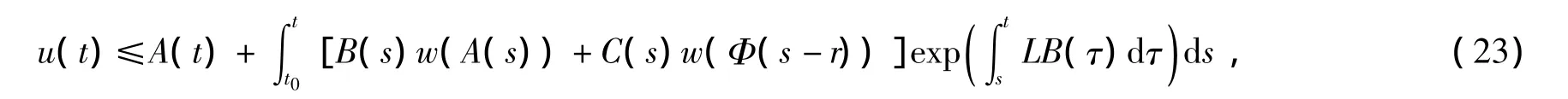
对任意t∈［t0+r，T)有估计式

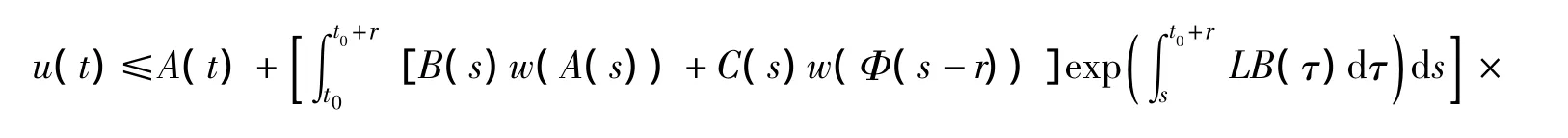
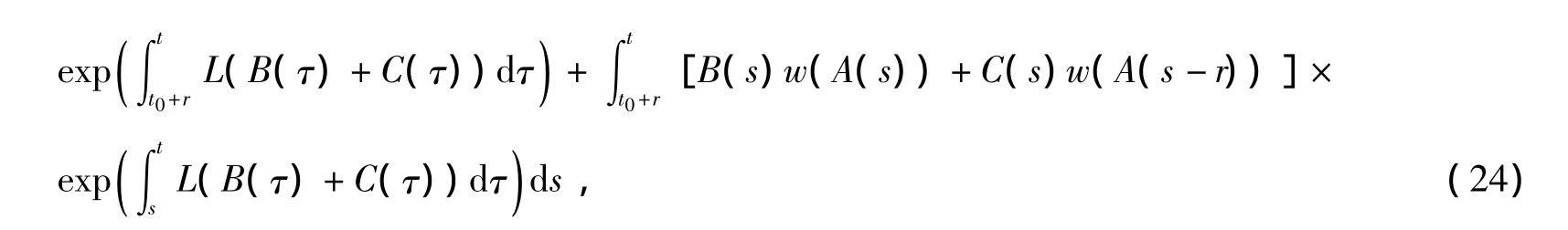
上式中，函数A(t)，B(t)，C(t)，Φ(t)分别由

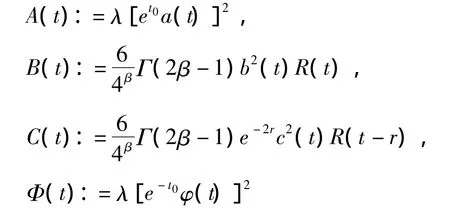
定义，其中λ=max{3，e2r}.

(2)当β∈(0，1/2］，p=1+β时，对任意t∈［t0，t0+r)有估计式

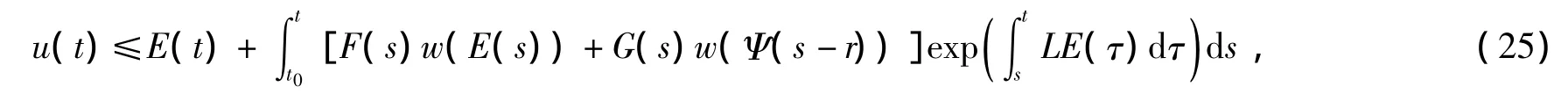
对任意t∈［t0+r，T)有

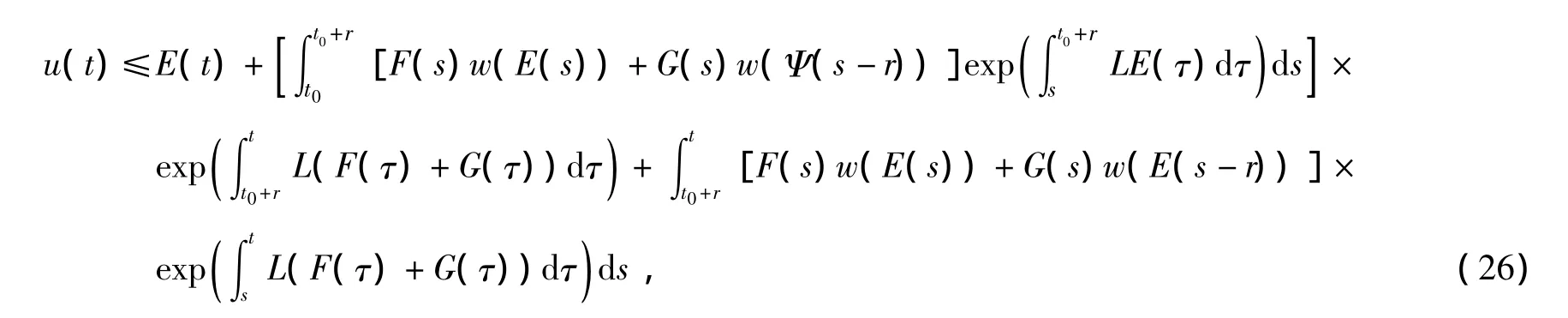
上式中，函数E(t)，F(t)，G(t)，Ψ(t)分别由

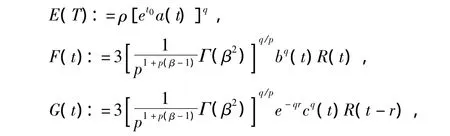
以及Ψ(t):=ρ［e-t0φ(t)］q定义，其中q=1+，ρ又由ρ=max{3，eqr}定义。

证明:(1)当β＞1/2时，对任意t∈［t0，T)，利用Cauchy-Schwarz不等式，由式(6)我们推出

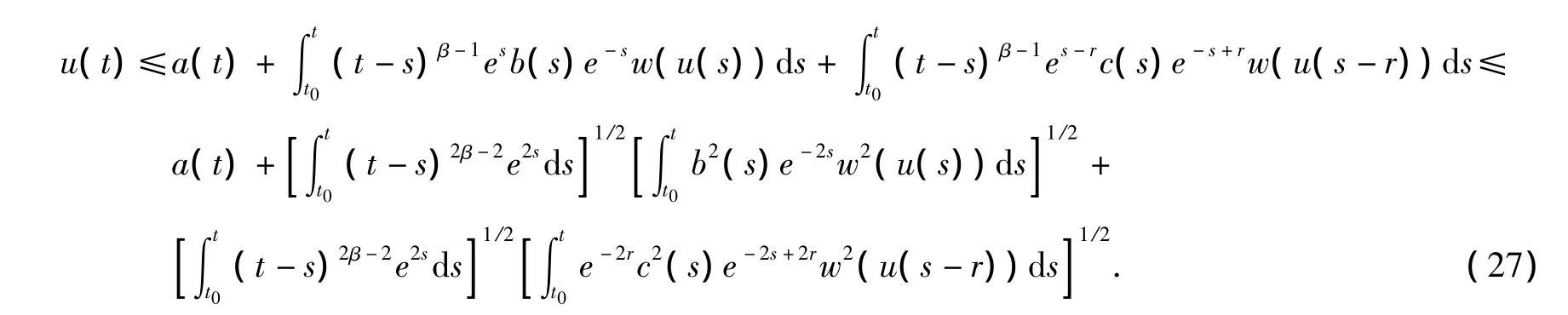
因为函数w满足(q)条件，利用定义1中的式(7)和引理1中的式(8)，由式(27)我们推出

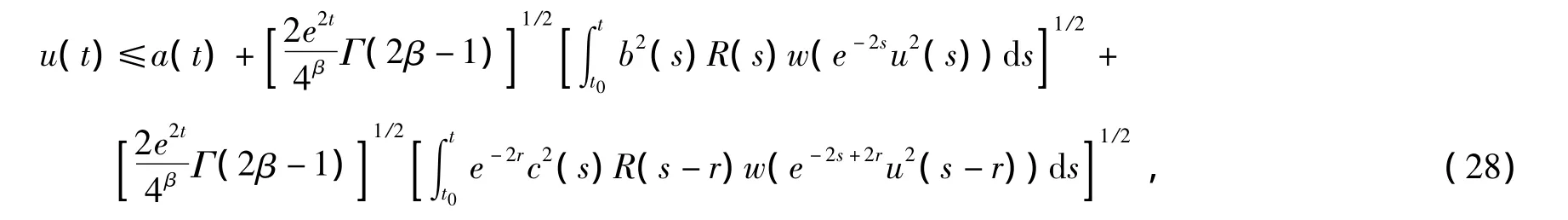
对于任意t∈［t0，T)成立。利用引理2中的Jensen不等式(10)，由式(28)我们得到

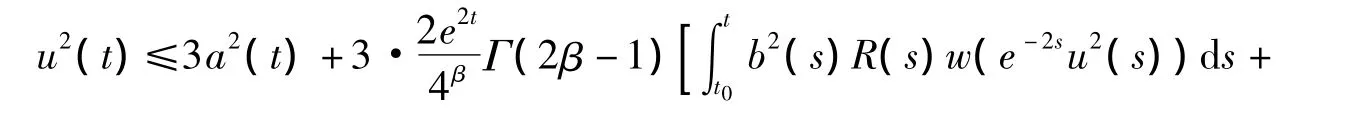
我们观察到当t∈［t0-r，t0)时，有v(t)=［e-tu(t)］2≤［e-tφ(t)］2≤e2r［e-t0φ(t)］2≤λ［e-t0φ(t)］2.根据函数A(t)，B(t)，C(t)的定义:

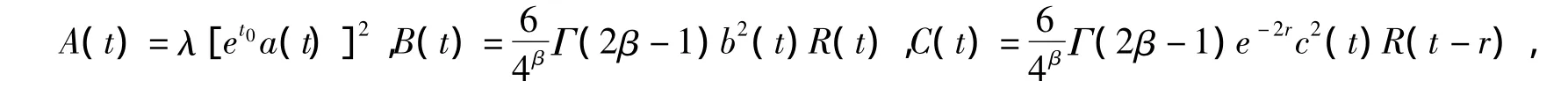
由式(30)我们看出

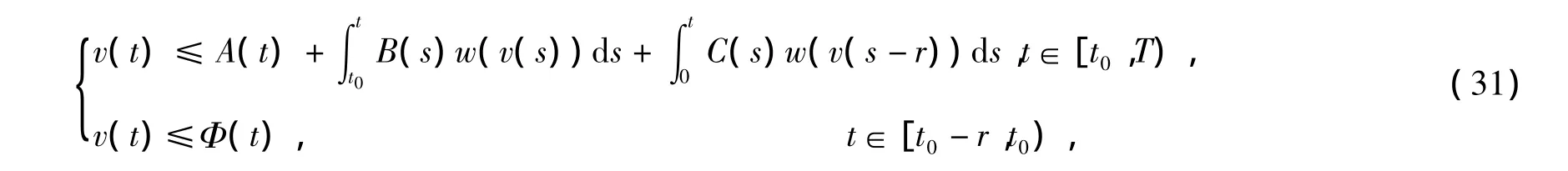
其中Φ(t)=λ［e-t0φ(t)］2.不等式(31)具有不等式(5)的形式，并且函数A(t)，B(t)，C(t)满足定理1中的相应条件。根据定理1，由式(31)，我们得到所要证明的结果式(23)和式(24)。

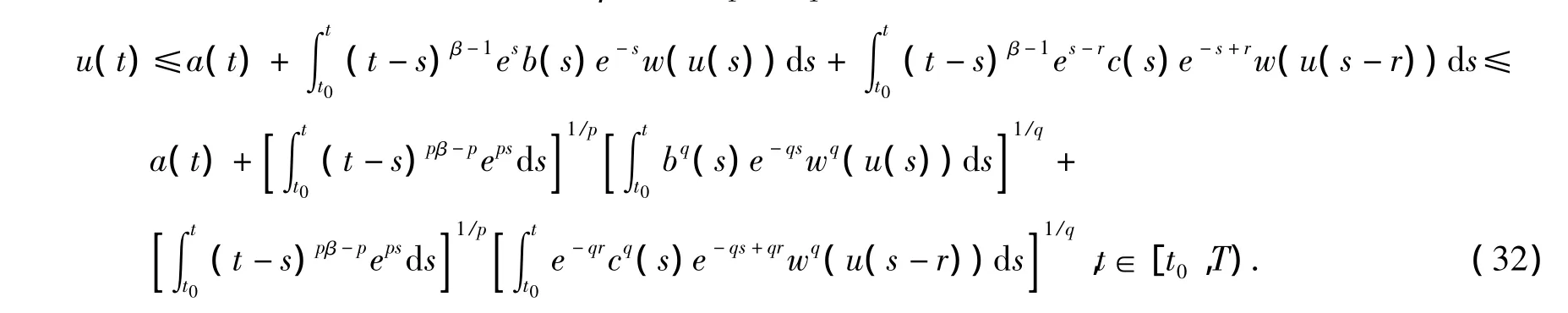
因为函数w满足(q)条件，利用定义1中的式(7)和引理1中的式(9)，由式(32)我们推出

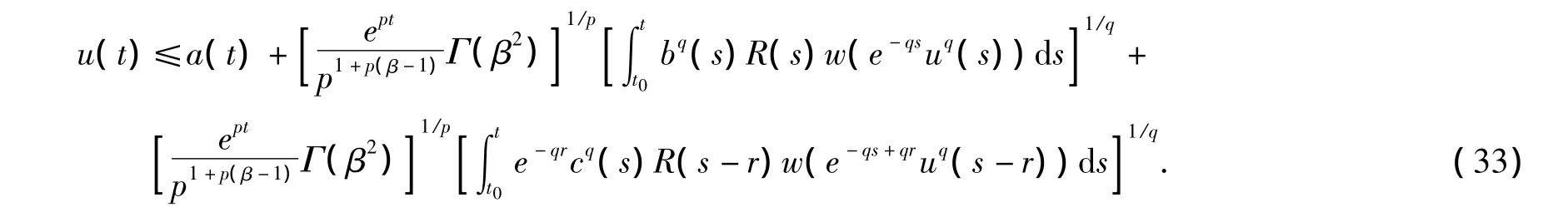
对于任意t∈［t0，T)成立。利用引理2中的Jensen不等式(11)，由式(33)我们得到

令v(t)=［e-tu(t)］q，ρ=max{3，eqr}，由式(34)我们有

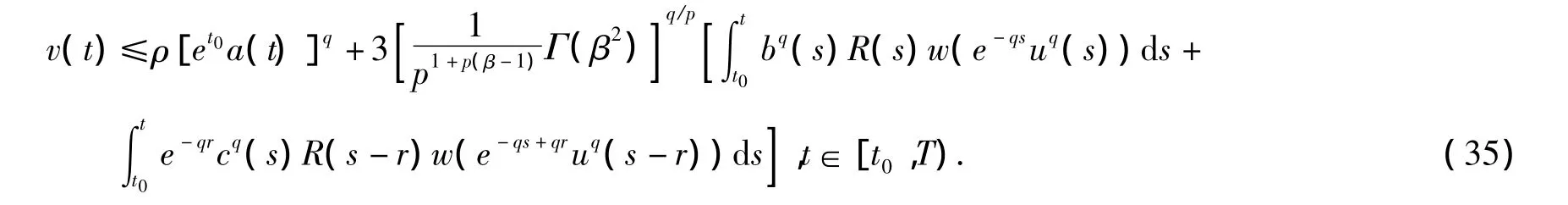
我们观察到当t∈［t0-r，t0)时，有v(t)=［e-tu(t)］q≤［e-tφ(t)］q≤eqr［e-t0φ(t)］q≤ρ［e-t0φ(t)］q.根据函数E(t)，F(t)，G(t)的定义:

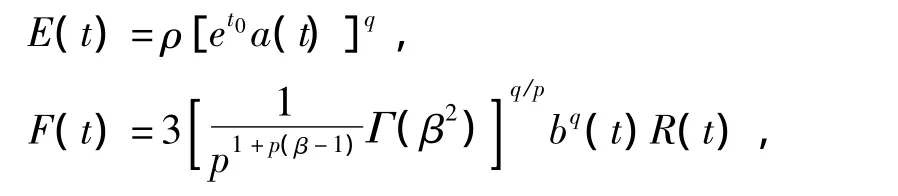
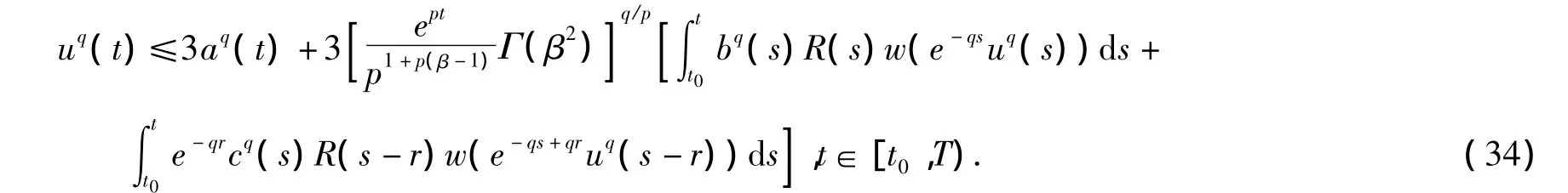
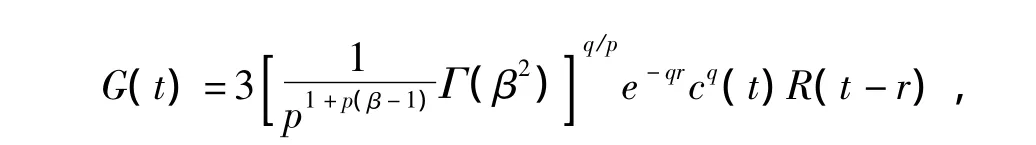
由式(35)我们看出

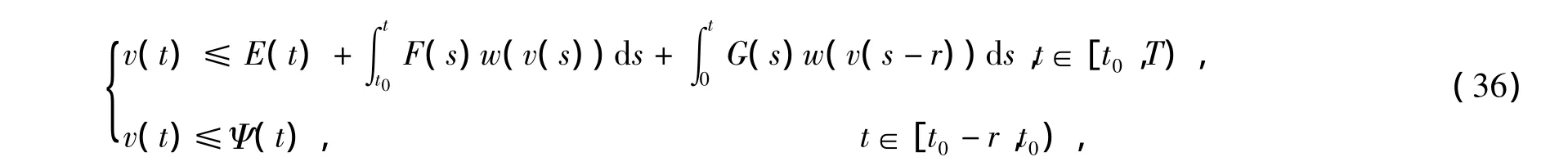
其中Ψ(t)=ρ［e-t0φ(t)］q.不等式(36)具有不等式(5)的形式，并且函数E(t)，F(t)，G(t)满足定理1中的相应条件，根据定理1，由式(36)，我们得到所要证明的结果式(25)和式(26)。

［1］ Gronwall T H.Note on the derivatives with respect to a parameter of the solutions of a system of differential equations［J］.Ann Math，1919，20:292-296.

［2］ Bellman R.The stability of solutions of linear differential equations［J］.Duke Math J，1943，10:643-647.

［3］ Bihari I A.A generalization of a lemma of Bellman and its application touniqueness problem of differential equation［J］.Acta Math Acad Sci Hung，1956，7:81-94.

［4］ Ye H，Gao J.Henry–Gronwall type retarded integral inequalities and their applications to fractional differential equations with delay［J］.Applied Mathematics and Computation，2011，218:4 152-4 160.

［5］ Medved M.A new approach to an analysis of Henry type integral inequalities and their Bihari type versions［J］.J Math Anal Appl，1997，214:349-366.

［6］ M Kuczma.An introduction to the theory of functional equations and inequalities:Cauchy’s equation and Jensen’s inequality［M］.Katowice:U-niversity of Katowice，1985.

［7］ Wlter W.Differential and Integral Inequalities［M］.Berlin，Ner York:Springer-Verlag，1970.

［8］ B G Pachpatte.Comparison theorems related to a certain inequality used in the theory of differential equations［J］.J Math，1996，22:383-394.

［9］ Medved M.On singular versions of Bihari and Wendroff-Pachpatte type integral inequalities and their application［J］.Tatra Mt Math Publ，2007，38:163-174.

［10］ Ye H，Gao J，Ding Y.A generalized Gronwall inequality and its application to a fractional differential equation［J］.J Math Anal Appl，2007，328:1 075-1 081.