钢-混凝土曲线组合梁弯扭性能的试验研究

， ，

(1.石家庄铁道大学 土木工程学院，河北 石家庄 050043；2.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室，河北 石家庄 050043)

0 引言

钢-混凝土组合梁具有承载能力大、刚度大、自重轻等优点，在桥梁结构中得到了广泛应用。由于道路线形的要求，通常需要将组合梁桥设计为曲线组合梁桥，因此会产生弯剪扭的复合作用。曲线组合梁在钢梁内部需设置横向连接系，国外通常选用内部撑杆，即“桁架式”，我国则常采用横隔板，即“隔板式”。

关于曲线组合梁的弯扭效应已有较多研究。Thevendran et al[1-2]对5片不同曲率的工字型简支曲线组合梁进行了模型试验和非线性分析；lee et al[3]分析了扭矩作用下双T形截面组合梁的受力性能；Tan 和Uy[4-5]对8片工字型简支曲线组合梁进行了弯扭试验研究；Kim et al[6]研究了“桁架式”钢-混凝土组合箱梁的弯扭相关作用；聂建国 等[7-8]和张彦玲 等[9]分别进行了“隔板式”钢-混凝土直线组合箱梁的弯扭试验。可以看出，目前关于“隔板式”曲线组合梁的研究还很少，我国各种规范中也无具体规定。

针对隔板式钢-混凝土曲线组合梁，进行了跨中集中荷载下的受力全过程加载试验，测试了其典型截面钢梁及混凝土板的应变、变形、以及结合面相对滑移规律，并分析了跨径比(计算跨径L与曲线半径R的比值)和横隔板数目对其产生的影响。

1 试验设计及加载方案

1.1 试验目的及内容

试验目的是为了研究曲线组合梁的弯扭受力特性，以及跨径比和横隔板数目对其产生的影响。试验内容包括：①不同跨径比和横隔板数目下曲线组合梁的破坏形态和极限承载力；②不同荷载水平下截面应变沿高度和宽度方向的分布规律；③结合面滑移变形分布规律。

1.2 试验设计与制作

以跨径比和横隔板数目为参数，设计了6片钢-混凝土简支曲线组合梁。跨度均为6 000 mm，全长6 200 mm；混凝土板宽度为700 mm，厚度为70 mm；钢梁高200 mm，下翼缘宽400 mm，上翼缘宽60 mm，上下翼缘厚度均为8 mm，腹板厚度6 mm。钢梁均采用Q235钢，混凝土板采用C30混凝土；纵筋与箍筋采用 HPB235钢筋，纵筋横向间距120 mm，配筋率0.81%；箍筋纵向间距100 mm，配箍率0.27%。栓钉直径13 mm，高50 mm，布置在钢梁腹板上方，每列34个，每片梁布置两列，共68个，均为完全连接。各试验梁沿跨度方向设置不同数量的横隔板，厚6 mm。试验梁参数见表1，截面尺寸见图1。

表1 试验梁参数

表1中各梁横隔板的位置为：2块横隔板的均设置在梁端支座处；3块横隔板的设置在两个梁端及跨中处；5块横隔板的设置在支座、跨中和两个1/4跨度处。

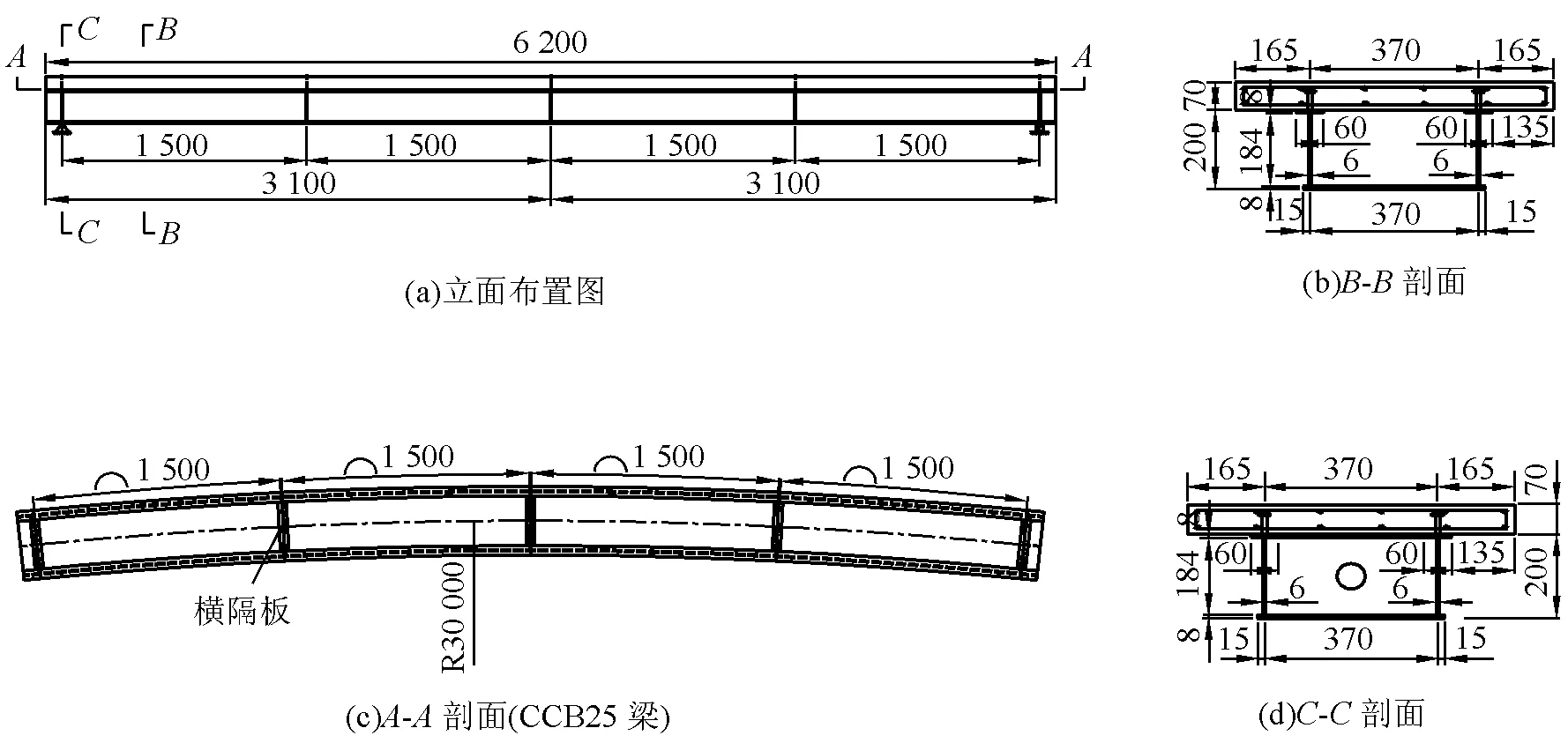
图1 试验梁截面尺寸及布置详图(单位：mm)

1.3 试验装置及加载方案

各试验梁均采用跨中加载。支承条件为一端设固定铰支座，一端设活动铰支座，每个支座下方均在钢梁腹板位置设置传感器以测试支座反力。CCB55梁由于跨径比较大，在曲线内侧支座出现负反力，因此设计了反力架，将曲线内侧支座传感器设置在腹板上方，其他五片试验梁及CCB55梁曲线外侧的支座传感器均设置在腹板下方，见图2和图3。

荷载分级施加，初期每10 kN荷载记录一次数据，并实时记录跨中截面的荷载-挠度曲线，当曲线斜率开始发生变化时，荷载等级减小为5 kN。加载过程中注意检查钢梁是否屈服，及混凝土板的裂缝开展情况，当混凝土有明显压碎或挠度过大时停止加载。试验过程中测试支座截面、L/8、L/4、3L/8和跨中截面(为避开加载位置，偏移20 cm)钢梁及混凝土板应变、竖向及径向位移、以及钢梁与混凝土板之间的相对滑移。加载布置图见图4。测点布置图见图5。

图2 支座布置图(除CCB55梁) 图3 CCB55梁支座布置图 图4 加载布置图

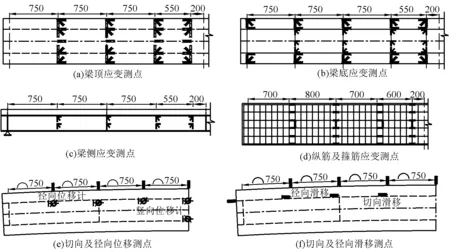
图5 测点布置图(单位：mm)

2 试验结果分析

2.1 破坏过程及受力特性

各试验梁跨中截面的荷载-挠度曲线如图6所示。

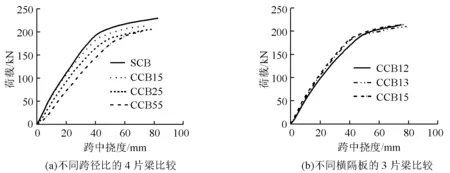
图6 跨中荷载-挠度曲线的比较

由图6可以看出：①不同跨径比和横隔板数目的试验梁，其全过程受力特征均经历了弹性阶段-弹塑性阶段-塑性阶段的发展过程；②横隔板数目相同时，直线梁的抗弯刚度、极限荷载和屈服荷载都最大，随跨径比增加上述指标均逐渐减小，跨径比为0.5的CCB55梁最小，说明跨径比的增大使曲线组合梁抗弯刚度下降，承载力降低；③跨径比相同时，横隔板数目的不同对曲线组合梁的整体弯曲受力性能影响不大，但从图中仍能够显示只有两个端横隔板的CCB12梁的刚度较其他两片有中横隔板的CCB13和CCB15梁略有减小；而CCB13和CCB15梁之间则几乎没有差别。

5片曲线组合梁跨中截面的荷载-扭转角曲线和荷载-径向位移曲线如图7和8所示。

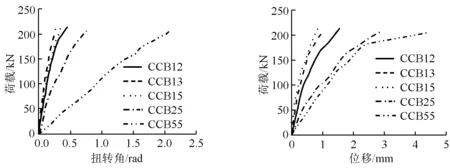
图7 跨中荷载-扭转角曲线 图8 跨中径向荷载-位移曲线

由图7可知，相同荷载下，随着跨径比的增大，跨中截面扭转角也随之增大，说明截面扭转刚度随跨径比的增大而减小；跨径比均为0.1，但横隔板数目不同的3片梁曲线比较接近，只设两个端横隔板的CCB12梁扭转刚度最小，但横隔板数目对跨中截面扭转角影响不大。

从图8可知，相同荷载下，跨中截面的径向位移随着跨径比的增大而增大；跨径比均为0.1的3片梁因横隔板数量不同，径向位移也略有差别，随着横隔板数量的增加，径向位移随之减小。

2.2 应变测试结果

2.2.1 切向应变沿截面竖向的分布

六片试验梁距跨中截面20 cm处在各级荷载下曲线外侧的切向应变沿截面高度的变化如图9所示，图中Pu指极限荷载。

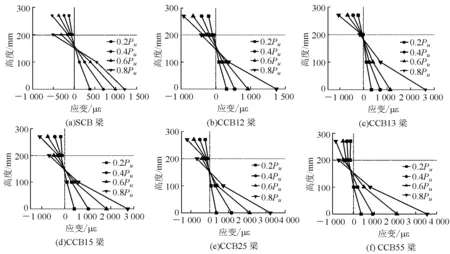
图9 切向应变沿截面竖向的分布

由图9可知：①在0.6Pu之前，切向应变沿截面竖向的分布近似为一条直线，到0.8Pu时钢梁下翼缘的应变增加较多，但整体上切向应变沿截面竖向基本符合平截面假定；②虽然试验梁均采用了完全连接，但从应变图中可以看出，在钢梁与混凝土结合面处，切向应变图形都出现了不同程度的水平台阶，说明结合面存在相对滑移；③由于图中所示为试验梁曲线外侧跨中截面附近的切向应变，因此从图中大致可以看出，随跨径比增大，切向应变有增大的趋势。

2.2.2 切向应变横向分布

分析横隔板数相同(均为5块)，跨径比不同的4片试验梁(SCB、CCB15、CCB25、CCB55)，在50 kN跨中集中荷载作用下，钢梁底板、混凝土板上表面和上层钢筋(沿宽度方向共6根)的切向应变沿截面横向分布的规律。

(1) 距跨中截面20 cm处。距跨中截面20 cm处没有横隔板，SCB、CCB15、CCB25、CCB55梁的切向应变如图10所示，图中横坐标y表示横截面上混凝土上表面或钢梁下表面距曲线内侧边缘的距离，以下同。由图10可知，在相同荷载下，距跨中截面20 cm处钢梁底板、混凝土板上表面和上层钢筋的切向应变均随跨径比的增大而增大，且沿截面宽度方向均表现出曲线内侧较大，曲线外侧较小的趋势，与一般曲线梁竖向荷载下受力曲线外侧大、内侧小的受力特性有所区别。其中直线的SCB梁切向应变沿截面横向基本对称，但也呈现中间小两端大，表现出一定的剪力滞现象。其他曲线梁则随跨径比的增大，切向应变沿截面横向的不均匀性渐趋明显。

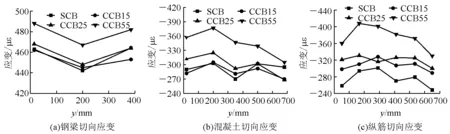
图10 距跨中截面20 cm处切向应变的横向分布

(2)L/4截面处。L/4截面处设有横隔板，该截面SCB、CCB15、CCB25和CCB55梁的切向应变如图11所示。 由图11可知，设有横隔板的L/4截面，其钢梁底板、混凝土上表面和上层纵筋的切向应变均随跨径比的增大而增大，除直梁SCB仍沿截面横向基本为对称分布外，其他三片梁均与没有横隔板的距跨中截面20 cm处截面的应变分布不同，呈现出内侧小外侧大的分布规律，这一点与一般曲梁在曲线内侧应力小，外侧大的弯扭耦合特征相同。

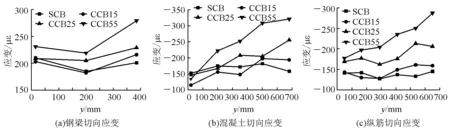
图11 L/4截面切向应变的横向分布

(3)3L/8截面处。3L/8截面处没有横隔板，处于有横隔板的跨中截面和L/4截面之间，该截面SCB、CCB15、CCB25和CCB55梁的切向应变如图12所示。 由图12可知，3L/8截面的切向应变分布与有横隔板的L/4截面有明显差别。钢梁底板、混凝土上表面和上层钢筋的切向应变均表现出相反的分布规律，即曲线内侧大，而曲线外侧小，且随跨径比的增加，切向应变沿截面横向分布的不均匀性增大。

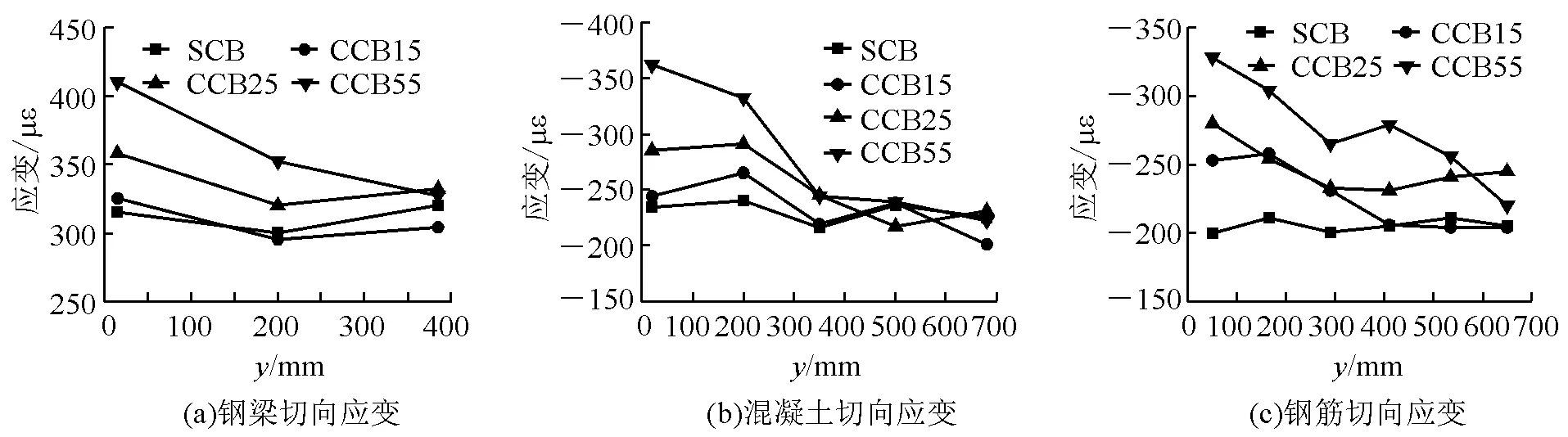
图12 3L/8截面切向应变的横向分布

(4)L/8截面处。L/8截面处也没有横隔板，处于有横隔板的L/4截面和支座截面之间。该截面SCB、CCB15、CCB25和CCB55梁的切向应变如图13所示。由图13可知，没有横隔板的L/8截面和3L/8截面相同，钢梁底板、混凝土上表面和上层钢筋的切向应变也表现出曲线内侧大，曲线外侧小的趋势，且随跨径比的增大，切向应变沿截面横向分布的不均匀性增大。

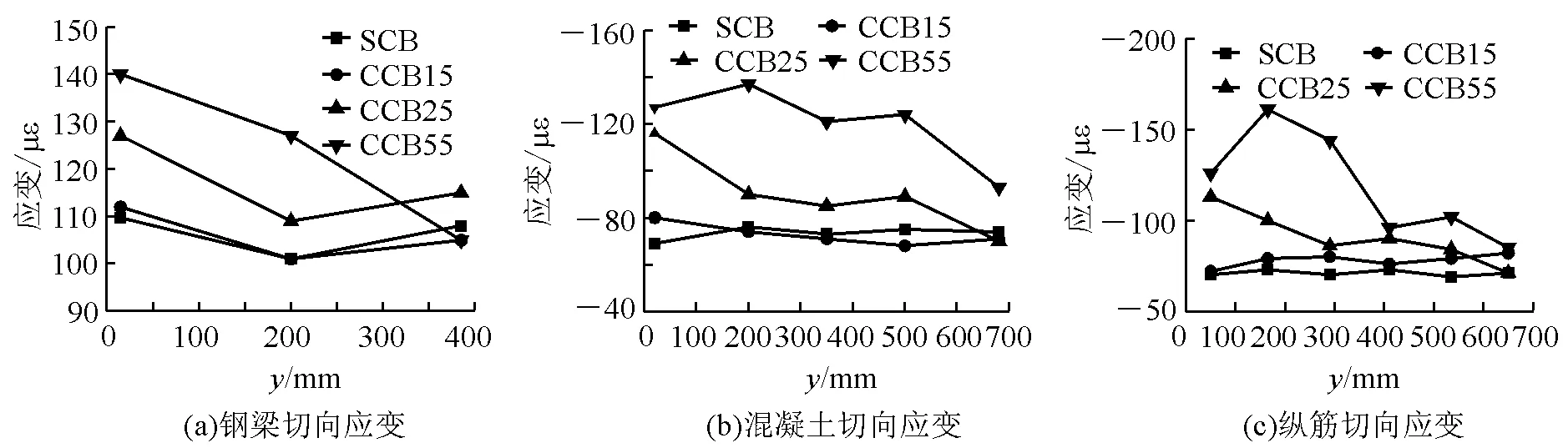
图13 L/8截面切向应变的横向分布

由以上分析可知，有横隔板的L/4截面与没有横隔板的其他三个截面，其切向应变沿截面横向的分布规律是不同的，有横隔板时切向应变在曲线内侧小，外侧大，与一般曲线梁的受力规律相同，而无横隔板处却完全相反。这是由于曲线组合梁在竖向荷载下除产生竖向变形外，还产生扭转变形和径向变形，而横隔板在扭转和径向变形过程中起到了一种弹性约束作用，在有横隔板的位置，由于弹性约束的影响切向应力增大，而无横隔板的位置处于相邻两个横隔板产生的弹性约束之间，反而有一种“卸载”的趋势，这种现象在曲线外侧和曲线内侧正好相反，因此出现有横隔板处切向应力在曲线内侧小外侧大，而无横隔板处则内侧大外侧小。无论有无横隔板，切向应变随跨径比的增大而增大。

2.3 滑移测试结果

各试验梁在L/8截面曲线外侧钢梁与混凝土板之间的相对切向滑移随荷载的变化规律见图14。

图14 荷载-切向滑移曲线

由图14可知：①对于跨径比均为0.1的3片试验梁，切向滑移非常接近，3条荷载-滑移曲线几乎重合，其中CCB12梁由于横隔板数量最少，滑移量与存在中横隔板的CCB13和CCB15相比较大；②对于横隔板数目相同(均为5块横隔板)，但跨径比不同的4片试验梁，在相同荷载下，随着跨径比的增大，相同位置的滑移逐渐增大。直线梁的最大滑移量最小，为0.63 mm；跨径比为0.5的CCB55梁最大滑移量最大，为1.25 mm。

各试验梁在不同荷载下切向滑移沿梁轴的分布规律如图15所示，图中横坐标x表示距梁端的距离。

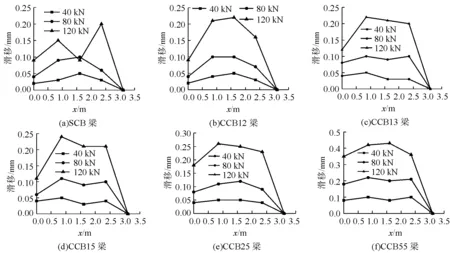
图15 切向滑移沿轴向的分布

由图15可以看出，随着荷载增大，切向滑移随之增大。6片试验梁切向滑移沿梁轴的分布规律基本相同，由于切向滑移是栓钉受到钢梁与混凝土板结合面上的水平剪力所致，而结合面水平剪力和梁截面竖向剪力之间存在线性关系，因此对于等截面梁，理论上切向滑移沿梁轴的分布与竖向剪力沿梁轴的分布规律相同。图中显示的切向滑移沿梁轴的分布规律与承受跨中集中荷载的试验梁的竖向剪力基本相同，但由于支座处的反力增加了混凝土板与钢梁结合面上的局部压力，使摩擦力增大，抑制了该处的滑移，因此梁端滑移反而较小。

3 结论

以跨径比和横隔板数量为参数，进行了6片简支曲线组合梁的模型试验，所得的主要结论如下：

(1) 钢-混凝土板曲线组合梁极限荷载、屈服荷载和跨中截面扭转角均随跨径比的增加逐渐减小，说明跨径比的增大使曲线组合梁抗弯刚度和抗扭刚度都随之下降；横隔板数目的不同对曲线组合梁的整体弯曲受力性能影响不大，但端横隔板对跨中截面扭转角影响较大，中横隔板影响较小。

(2) 在0.6Pu之前，切向应变沿截面竖向的分布近似为一条直线，到0.8Pu时钢梁下翼缘的应变增加较多，但整体上切向应变沿截面竖向基本符合平截面假定；在钢梁与混凝土结合面处，切向应变图形都出现了不同程度的水平台阶，说明结合面存在相对滑移；随跨径比增大，曲线外侧切向应变有增大的趋势。

(3) 有横隔板的截面与没有横隔板的截面相比，其切向应变沿截面横向的分布规律不同，有横隔板时切向应变在曲线内侧小，外侧大，无横隔板处则相反；无论有无横隔板，切向应变均随曲梁跨径比的增大而增大。

(4) 钢梁与混凝土板结合面上的切向滑移随跨径比的增大而增大，横隔板数目对其影响很小。切向滑移沿梁轴的分布规律与承受跨中集中荷载的试验梁的竖向剪力基本相同，但由于支座处的反力增加了混凝土板与钢梁结合面上的局部压力，使摩擦力增大，抑制了该处的滑移，因此梁端滑移反而较小。

参 考 文 献

[1]Thevendran V, Chen S, Shanmugam NE, et al.Nonlinear analysis of steel-concrete composite beams curved in plan[J]. Finite Elements in Analysis and Design, 1999, 32:125-139.

[2]Thevendran V, Chen S, Shanmugam NE, et al.Experimental study on steel-concrete composite beams curved in plan[J]. Engineering Structures, 2000, 22: 877-889.

[3]Lee Y H,Sung W J,Lee T H, et al. Finite element formulation of a composite double T beam subjected to torsion[J]. Engineering Structures, 2007, 29(11): 2935-2945.

[4]Tan E L,Uy B. Experimental study on straight composite beams subjected to combined flexure and torsion[J]. Journal of Constructional Steel Research, 2009, 65(4): 784-793.

[5]Tan E L,Uy B. Experimental study on curved composite beams subjected to combined flexure and torsion[J]. Journal of Constructional Steel Research, 2009, 65(8/9): 1855-1863.

[6]Kim K,Yoo C H. Ultimate strength interaction of bending and torsion of steel-concrete composite trapezoidal box girders in positive bending[J]. Advances in Structural Engineering, 2006, 9(5): 707-718.

[7]胡少伟, 聂建国, 朱林森. 钢-混凝土组合梁复合弯扭作用下非线性分析[J]. 工程力学, 2005, 22(2): 1-5, 26.

[8]聂建国, 唐亮, 胡少伟, 等. 钢-混凝土组合箱梁的抗扭强度[J]. 土木工程学报, 2008, 41(1): 1-11.

[9]张彦玲, 葛威, 侯忠明, 等. 弯扭联合作用下钢-混凝土组合箱梁受力特性的试验研究[J]. 石家庄铁道大学学报: 自然科学版, 2012, 25(4): 1-6.