我国燃油期货市场成交量和持仓量对价格波动的影响研究

冯梦黎，马箐箐

(成都理工大学 商学院，成都 610051)

一、引言

为了尽快地融入国际燃油定价体系，2004年8月上海期货交易所正式推出了燃料油期货交易，以此减轻我国在应付国际燃油市场上油价的大幅振荡风险带来的损失。虽然我国燃油期货市场发展至今已将近十年，但目前我国对燃油期货市场的了解和认识仍处于起步阶段，对其内部结构、运行特征的研究也非常缺乏。在期货市场上，反映期货市场行情的最为重要的几个因素分别是价格、成交量和持仓量。研究燃油期货成交量、持仓量对价格波动的影响，有助于了解燃油成交量和持仓量在燃油期货价格波动中所起的作用，有助于了解燃油期货市场的内部结构和对信息的反应程度，并最终达到控制燃油期货市场风险的目的，以更好地促进我国燃油期货市场的发展。

燃油期货市场的价量关系长期以来都受到国内外学者的关注。大量的文献研究显示，燃油期货市场交易量和价格波动之间存在正相关关系，如Clark[1](1973)、Copeland[2](1976)、Karpoff[3](1987)、Karpoff[4](1988)、 Bessembinder和Seguin[5](1992)等都进行了相关研究。学者们在研究燃油交易量与价格波动的关系时，发现滞后期交易量与当期交易量对价格波动的影响并不相同。Foster[6](1995)、Wang和Yau[7](2000)研究发现，燃油价格波动与交易量成正相关，而与交易量滞后项之间存在负相关关系。随后，学者们进行了更深入和更全面的研究，发现不仅期货价格波动和交易量存在一定关系，同时，期货价格波动与持仓量也有一定的联系。Bessembinder和Seguin[8](1993)、Girma和Mougoue[9](2002)、Chan[10](2004)、Ragunathan[11](1997)等研究发现，交易量和收益率之间存在着强烈的正相关关系，而持仓量和收益率之间存在负相关关系。相较于国外学者，国内学者对燃油期货价格与交易量、持仓量的关系研究相对较晚。国内学者华仁海和仲伟俊[12](2004)、仲伟俊等[13](2008)对燃料油期货市场的成交量和持仓量对价格波动的影响作了详尽的分析，研究结果发现，交易量与价格呈正相关，持仓量与价格呈负相关。戴毓等[14](2009)研究表明，燃料油期货市场的成交量对价格波动具有非常强的解释性，也就是说，可以根据上一期的成交量预测下一期的价格波动；同时，当期持仓量增大时，期货价格波动将减小。崔海蓉等[15](2010)研究也发现，燃料油期货市场的价格与成交量呈正相关，持仓量与价格呈负相关。

由于燃油期货在我国推出的时间不长，国内学术界针对我国燃油期货市场成交量、持仓量对价格波动影响关系的研究还相对缺乏。为此，本文选取燃油期货合约为研究对象，研究其成交量和持仓量对价格波动的影响关系，以期可以更好地揭示出我国燃油期货市场的内在特征。同时，已有文献在进行建模时大多数并没有考虑期货价格波动率的非对称性，实证研究也运应用GARCH模型。因此，本文在建立模型时选取可以更好地反映金融时间序列对正负信息反应呈非对称性的EGARCH模型。另外，学者对燃油期货波动序列与成交量、持仓量建立模型时，一般默认模型的残差服从正态分布，然而实际情况往往并非如此。基于正态分布的模型仅部分解决了金融时间序列的中尖峰、厚尾的问题，为了更加准确地描述EGARCH模型中残差的分布特征，本文引入Student’s-t分布。本文拟分两种情况对三者之间的关系进行实证研究。第一是分别考察成交量、持仓量对我国燃油期货价格波动的影响，第二是同时考察成交量与持仓量对我国燃油期货价格波动的影响。

二、EGARCH实证分析模型的构建

由于期货价格具有异方差和对信息的非对称性，因此本文借用EGARCH模型可以很好地体现金融价格波动的杠杆效应，并且以条件方差的对数形式确保条件方差为正，使模型可以更规范和稳定。EGARCH(1,1)模型如下：

Rt=c+ARMA(p,q)+ut

(1)

(2)

为了研究成交量、持仓量对燃油期货价格波动性的影响，本文在EGARCH模型中引入成交量和持仓量。首先我们分别考察成交量、持仓量对我国燃油期货价格波动的影响；其次是同时考察成交量与持仓量对我国燃油期货价格波动的共同影响。本文把同期交易量和滞后一期交易量以及同期持仓量和滞后一期持仓量引入方差方程，令价格波动为Rt，Vt为连续合约在第t个交易日的成交量，It为连续合约在第t个交易日的持仓量，则得到如下模型：

Rt=c+ARMA(p,q)+utut～N(0,ht)

(3)

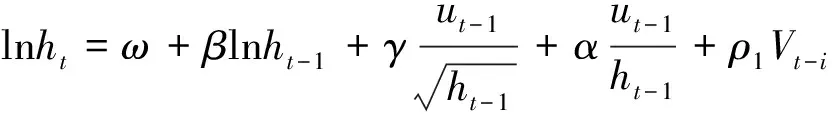
(4)

(5)

ρ1Vt-i+ρ2It-i

i=0,1

(6)

方程(4)中考虑了成交量对价格波动方差的影响，分别是当期和滞后期；方程(5)中考虑了持仓量对价格波动方差的影响，分别是当期和滞后期；而方程式(6)中同时考虑了当期成交量和滞后期持仓量对价格波动方差的影响，分别也是当期和滞后期。

另外，在对燃油期货波动序列与成交量、持仓量建立EGARCH模型时，一般默认模型的残差服从正态分布，然而实际情况往往并非如此，基于正态分布的EGARCH模型仅部分解决了金融时间序列的中尖峰、厚尾的问题。为了更加准确地描述 EGARCH模型中残差的分布特征，本文引入自由度为v的Student’s-t分布，即假定模型中的误差项服从如下的分布：

此时的模型即为EGARCH-t模型，t分布有更宽的尾部，能更好地描绘收益序列的后尾性特征。

三、燃油期货合约序列数据分析

(一)数据描述

本文研究的对象是我国燃油期货市场，采用的数据类型为燃油期货合约交易日内的交易量、持仓量和收盘价，数据的时间跨度为2004年10月15日至2013年11月20日。由于每个期货合约都将在某个时间内到期，因此，期货价格具有不连续的特征。另外，在同一交易日，会有许多个不同交割时间的期货合约在交易。因此，同一期货品种在同一交易日会同时有许多个不同交割时间的交易数据存在。所以我们需要对燃油期货合约数据进行处理，以建立一个连续的燃油期货合约序列。

华仁海和仲伟俊(2004)[12]以及崔海蓉等(2010)[15]根据期货品种的交易量、持仓量和交易活跃程度来选取期货合约代表来产生一个连续期货合约序列。但对于燃油期货而言，国内燃油期货市场还处于初生阶段，某些月份的数据有缺失或没有交易(如燃油期货在春节前后就不进行交割)。为此，本文在已有研究的基础上作出一些修改，对燃油期货合约按照如下方法来构造连续的燃油期货合约：选取最近期月份的期货合约的每天收盘价格和相对应的交易量、持仓量，在最近期货合约进入交割月后，选择下个最近期月份的期货合约。这样做是为了克服期货价格波动不稳定、交割月交易量较小的缺点。考虑到燃油期货数据的局限性，以每年9月份作为基准，同时剔除没有实际成交的数据后，燃油连续合约序列中数据的个数为1768个。

按照上述方法产生的连续期货合约的优点在于，所选择期货合约的期货价格序列、成交量序列和持仓量序列具有较好的代表性。由于期货价格波动较小，因此将会给数据处理带来一定的困难。所以，将价格波动Rt定义为：

Rt={Ln(Ft)-Ln(Ft-1)}×100

(7)

式中，Ft为连续合约在第t个交易日的收盘价格。

由于燃料期货合约在各个不同月份的成交量和持仓量可能相差很大，不利于反映价格波动的一般特点和比对价格波动，因此文中研究的成交量和持仓量分别取它们的自然对数。即：

LVt=Ln(Vt)-Ln(Vt -1)

(8)

LIt=Ln(It)-Ln(It -1)

(9)

因此，在方程(4)、(5)、(6)中用LVt替代Vt，LnIt替代It。

(二)数据平稳性检验

为了防止伪回归的现象，需要先对数据进行平稳性检验。本文运用ADF检验法，对Rt、LVt、LIt进行单位根检验(表1)。

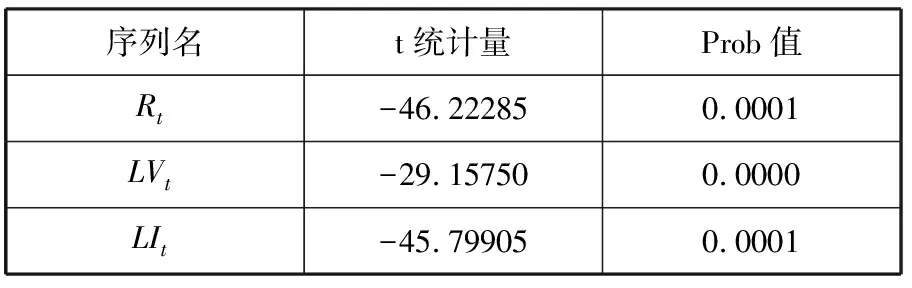
表1 Rt，LVt，LIt，ADF单位根检验

ADF检验结果显示，Rt、LVt、LIt各序列均为平稳序列，原序列在1%显著水平下拒绝含有单位根的假设，序列为典型的零阶单整时间序列。

四、成交量和持仓量对价格波动影响的实证分析

(一)价格的波动特征

1.价格波动的统计特征

表2给出了价格波动Rt序列的统计特征。从表2的统计结果可以看出，价格波动Rt序列的JB统计量表明它不满足正态分布，同时峰度大于3，呈现出明显的尖峰厚尾性和异方差性。

表2 Rt的基本统计量

2.EGARCH模型模拟价格的波动特征

运用EGARCH(1,1)模型模拟价格波动Rt的波动特征，由于呈现出明显的尖峰厚尾特征，并且数据量较大，因此运用Eviews7.0时选取的分布为Student’s-t分布。从表3结果可以看出，方差方程已不存在自相关，滞后1、2阶的LM值都很小，即残差序列不再有ARCH效应，EGARCH(1,1)模型已充分拟合了燃油期货市场价格波动Rt的特征。同时，β值很接近1且非常显著，说明燃油期货市场价格波动Rt的ARCH效应非常明显，其波动有明显的持续性和聚集效应。同时燃油期货市场的γ值为0.26，这说明燃油期货市场是存在一定的杠杆效应，利好和利坏消息对条件方差有一定影响。

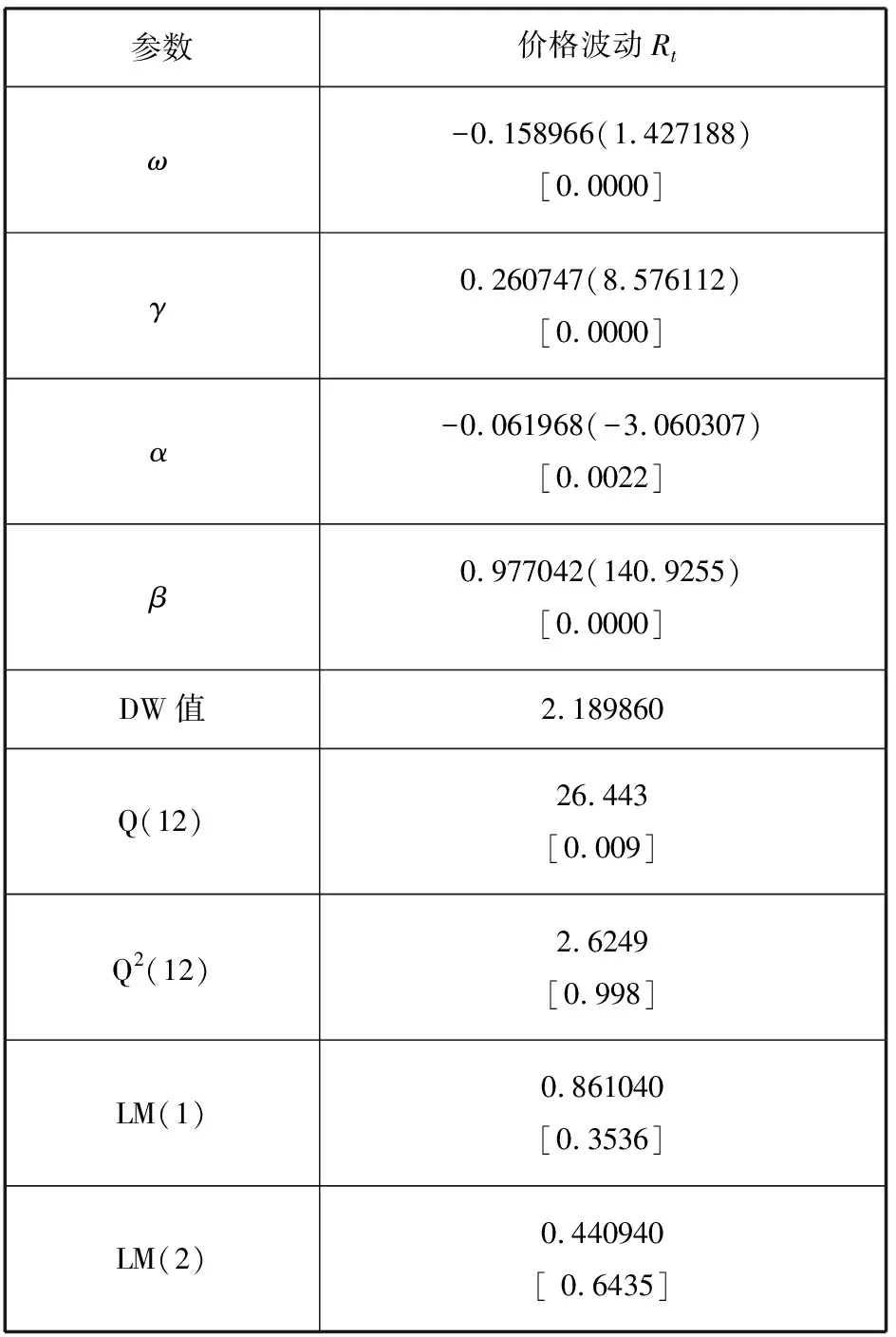
表3 价格波动EGARCH(1,1)方差方程的参数估计结果

注：①表中圆括号内为t统计量，中括号内为P值，当P<1%时，该参数的估计值显著；否则不显著。②Q(24)表示标准化残差滞后24阶的Ljung-Box修正Q统计量, Q2(24)表示平方标准化残差滞后24阶的Ljung-Box修正Q统计量，两个统计量均服从χ2(24)分布。Q(24)检验均值方程的残差的自相关性，Q2(24)检验残差平方的异方差性。③LM(1)、LM(2)表示滞后一阶和二阶残差的ARCH效应检验。

(二)价格波动与成交量相互关系分析

表4给出了在EGARCH(1,1)模型的方差方程中引入同期成交量和滞后一期成交量时的参数估计结果。如表4所示，在5%的置信水平下，在方差方程中加入同期成交量后，发现燃油期货市场同期成交量与价格波动的相关系数ρ1大于零，即同期成交量和价格之间有强烈的正相关关系，这与之前多位国内外学者得出的研究结论是一致的。同时，无论是加入同期还是滞后一期成交量，波动系数β变化很微弱，还是接近1，这说明波动的ARCH效应没有被成交量吸收，波动的聚集效应和持续性依旧很明显。在方差方程中加入滞后成交量后发现，燃油期货市场的ρ1不是特别显著，这说明滞后成交量与价格没有很明显的关系。而γ在5%的显著水平下很显著，说明燃油期货市场是存在一定杠杆效应的，利好和利坏消息对条件方差有一定影响。同时，γ为正，说明燃油期货市场价格对同等程度的利好消息反应更为强烈。

表4 同期和滞后一期成交量对价格波动的影响

(三)价格波动与持仓量相互关系分析

表5给出了在EGARCH(1,1)模型的方差方程中引入同期持仓量和滞后一期持仓量时的参数估计结果。如表5所示，在方差方程中加入同期持仓量后，在5%的置信水平下，发现同期持仓量与价格的相关系数ρ1小于零，即同期持仓量和价格之间有显著的负相关关系，这说明燃油期货市场当期持仓量的变化对价格波动具有一定的解释作用。当在5%的置信水平下，在方差方程中加入滞后持仓量后，燃油期货市场的ρ2不是特别显著，这说明滞后持仓量对价格波动没有很明显的影响。

表5 同期和滞后一期持仓量对价格波动的影响

(四)价格波动与成交量和持仓量相互关系分析

表6给出了在EGARCH(1,1)模型的方差方程中引入同期成交量和滞后一期成交量以及同期持仓量和滞后一期持仓量时的参数估计结果。如表6所示，当在EGARCH(1,1)模型中同时引入同期成交量和同期持仓量时，燃油期货市场成交量之前的系数ρ1大于零，且在5%的置信水平下统计量显著。这说明，在同时考虑当期成交量和当期持仓量对价格波动的影响时，当期成交量增大，当期期货价格的波动方差也增大；如果当期成交量减小，当期期货价格的波动方差也减小。在考察当期持仓量时，燃油期货市场成交量之前的系数ρ2小于零，这也就意味着：有A

表6 同期和滞后一期成交量、持仓量对价格波动的影响

五、研究结论

本文利用EGARCH模型对燃油期货的成交量和持仓量对期货价格的波动影响进行了研究。由于EGARCH模型可以反映金融时间序列对正负信息的非对称性，因而使所用模型更加客观、估计结果更加准确。通过本文实证分析，可以得到以下结论：

燃油期货存在对正负信息反应的不对称性，即在同等程度的消息反应中，价格对利好消息的反应更为强烈。在此基础上，在单独考察成交量和持仓量对期货价格波动方差的影响时，燃油期货市场当期成交量对价格波动方差具有较显著的影响，滞后成交量与持仓量对价格波动方差都没有很明显的影响。在同时考察成交量和持仓量对价格波动方差的影响时，有A

由于燃油期货市场的滞后成交量和持仓量对价格波动方差的影响都不明显，说明我国燃油期货市场运行效率较好；同时由于市场价格对信息的反应存在非对称性，在一定程度上可以根据当期交易量和持仓量的变化对燃油期货价格波动进行预测。这对燃油期货监管部门和交易者具有非常重要的意义，有利于他们把握燃油期货市场的价格走势，有效地规避风险。

参考文献：

[1]Clark P.A subordinated stochastic process model with finite variances for speculative prices[J].Econometrica，1973，(41)：135-155.

[2]Copeland，T.E.A model of asset trading under the assumption of sequential information arrival.Journal Of Finance，1976，(31)：1149-1168.

[3]Karpoff J M. The relation between price changes and trading volume：a survey[J].Journal of Financial and Quantitative Analysis，1987，(22)：109-126.

[4]Karpoff J M. Costly short sales and the correlation of returns with volume[J].Journal of Financial Research，1988，(1)1：173-188.

[5]Bessembinder H，Seguin PJ.Futures trading activity and stock price volatility[J].Journal of Finance，1992，47(5)：2015-2034.

[6]Foster A J.Volume-volatility relations for crude oil futures markets[J].Journal of Futures Markets，1995，(15)：929-951.

[7]Wang G HJ，Yau J. Trading volume，bid-ask spread，and price volatility in futures markets[J].Journal of Futures Markets，2000，20(10)：943-970.

[8]Bessembinder H， Seguin P J. Price Volatility， Trading Volume，and Market Depth： Evidence from Futures Markets [J].Journal of Financial and Quantitative Analysis，1993，(3).

[9]Girma P B， Mougoue M. An Empirical Examination of the Relation between Futures Spreads Volatility， volume， and Open Interest[J].Journal of Futures Markets，2002，22(11).

[10]Chan K C， Fung H G， Leung W K. Daily volatility behavior in Chinese futures markets[J].Journal of International Financial Markets，Institutions and Money，2004，14(5)：491-505.

[11]Ragunathan V， Peker A. Price volatility， trading volume， and market depth： evidence from the Australia futures markets[J]. Applied Financial Economics，1997，(7)：447-454.

[12] 华仁海，仲伟俊.我国期货市场期货价格波动与成交量和空盘量动态关系的实证分析[J].数量经济技术经济研究，2004，(7)：123-132.

[13] 仲伟俊，刘庆富，梅妹娥.中国期市波动性与收益率、交易量和空盘量的关系[J].系统工程学报,2008，23(4)：508-512.

[14戴毓，周德群.燃料油期货市场成交量、持仓量与波动性关系[J].系统工程理论与实践,2009，29(12)：154-162.

[15]崔海蓉，何建敏.我国期货市场成交量和持仓量与价格波动关系研究[J].统计与决策，2010，(6)：127-129.