沪深300股指期货套期保值效率度量研究——基于沪深300ETF的实证分析

王继莹，郑耀威

( 吉林大学 商学院 ，长春 130012)

一、引言

套期保值是股指期货最重要的功能，其基本思想是根据合理的比例配置相反的期货和现货头寸，使二者的盈亏相抵消，从而使价格风险降低到最低程度。而沪深300股指期货自2010年4月推出以来，套期保值功能发挥的效率如何，能否有效地规避现货市场风险，是值得深入研究的内容。

相对而言，国外对这方面的研究起步较早，研究也比较深入，早期主要基于静态模型研究。Herbst[1](1989)and Myers[2](1989)提出双变量向量自回归模型(B-VAR)，其目的是为了弥补OLS模型中残差自相关造成的误差。Ghosh[3](1993)则是考虑两个时间变量之间的协整关系，并基于此运用ECM模型对股票套期保值比率和效果进行研究，并发现效果优于普通OLS得到的套期保值比率。伴随着GARCH模型的问世，学者们开始着眼于建立动态套期保值比率估计模型。Garcia[4](1997)和Roh,Yeh and Gannon[5](2000)的研究都是基于GARCH族模型，而其结果也大都反映了GARCH 族模型相对其他早期模型的优越性。之后，Hsu,Tseng and Wang[6](2008)提出了一系列基于GARCH的最优套期保值比率的估计模型，包括传统静态的GARCH、不变的条件相关GARCH、动态条件相关的GARCH模型。实证结果显示，基于Copula的GARCH模型比其他动态模型更有效。

而国内学者对沪深300股指期货套期保值功能的研究，则是主要借鉴国外成熟的模型，其根本基于风险最小化即方差最小化的框架对最优套期保值比率进行估计，并评估套期保值效果。高辉、赵进文[7](2007)运用OLS/VAR以及ECM模型对沪深300股指期货套期保值比率进行研究，并检验不同模型下套期保值的有效性。吴先智[8](2008)基于仿真交易数据对沪深300股指期货的套期保值进行研究，得出GARCH模型更适合用于估算套期保值比率的结论。陈守东、胡铮洋和孔繁利[9](2008)发现，ECM 模型估计的最优套期保值比率比OLS模型估计的比率稍大，但两者的套期保值效果相当。朱志红、王向荣[10](2011)基于2010年沪深300股指期货真实交易数据，运用OLS、ECM以及GARCH模型，分别估计最优套期保值比率，发现期货市场的盈利能较大程度地弥补现货市场的亏损，套期保值的效果显著。吴春来[11](2012)也基于沪深300股指期货真实交易数据并运用多种模型进行最优套期保值比率的研究。他同样认为，GARCH模型所得出的套期保值比率最优。蒋彧[12](2013)通过构建GARCH-Copula模型估计股指期货套期保值比率，并发现在股票价格指数上升阶段的套期保值比率要低于下降时股指套期保值比率。

虽然目前存在着大量关于沪深300股指期货套期保值功能的研究，但运用期货真实交易数据的研究并不多，且选用的现货标的一般为沪深300指数本身或股票、ETF组合。这两种现货标的皆有一定的缺陷：一方面沪深300指数并不可直接交易，另一方面股票或ETF所构建的组合可能会出现成本高、跟踪误差大的特点，而2012年5月推出的沪深300ETF恰恰为套期保值的研究提供了完美的可交易现货标的。因此，本文基于多种套期保值比率估计模型，以沪深300ETF为现货标的进行套期保值研究，度量我国沪深300股指期货的套期保值效率，并力图寻找效果最优、最符合市场实际运行情况的套期保值比率估计模型，为投资者实现风险规避提供借鉴与参考。

二、套期保值比率估计模型介绍

(一)静态套期保值比率估计模型

学术界早期对期货套期保值比率的研究是静态的，所估计出的最优套期保值比率是固定不变的，主流模型有以下几种：

1.简单线性回归模型(OLS)

建立线性回归方程：

ΔSt=α+βΔFt+εt

(1)

其中，ΔSt为现货价格的变化，ΔFt为相应的期货价格的变化，随机误差项εt～i.i.d，且服从N(0,σ2)，斜率β的估计值即为最优套期保值比率h*，即

(2)

2.二元向量自回归模型(B-VAR)

简单的线性回归模型假设随机误差项独立且服从N(0,σ2)，但实际情况中，随机误差项往往会存在序列相关性和异方差性，这可能会使通过OLS方程得到的最优套期保值比率存在一定风险。为了克服随机误差项的序列相关性，可以运用二元自回归模型B-VAR来估计最优套期保值比率，建立方程如下：

(3)

(4)

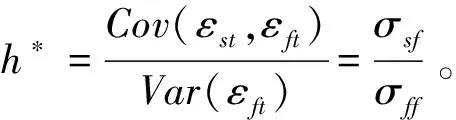
3.向量误差修正模型(VECM)

根据Engle，Granger提出的协整理论，当期货价格与现货价格存在协整关系时，运用OLS的估计量将是有偏的，忽略了前期均衡误差的影响的B-VAR模型也不能有效刻画二者之间的长期均衡关系，因此在B-VAR中加入误差修正项Zt-1。

(5)

(6)

一般情况下，Zt-1=St-1-λFt-1，其系数λs和λf不同时为零。估计得出最优套期保值比率Rf。

(二)动态套期保值比率估计模型

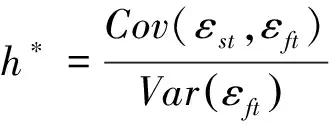
1.误差修正二元GARCH模型(VECM-BGARCH)

VECM-BGARCH模型既考虑了期货价格和现货价格之间的协整关系，也考虑了二者价格序列波动存在的异方差问题。

建立均值方程：

(7)

条件方差方程为：

(8)

如果系数矩阵是对角矩阵，则条件方差可简化为：

(9)

(10)

hsf,t=Csf+αsfεs,t-1εf,t-1+βsfhsf,t-1

(11)

该模型要估计的参数比较多，且很难维持正值，即使全部为正值，也不一定能够使条件方差-协方差矩阵满足正定。

2.DBEKK-GARCH模型

Engle，Kroner提出一类新的GARCH模型(BEKK-GARCH)，该类模型是建立在Baba，Engle，Kraft and Kroner所研究模型的基础上，该模型满足了条件方差-协方差矩阵的正定性，并减少了待估参数。该模型均值方程为：

(12)

条件方差方程为：

(13)

若假定系数矩阵均为对角矩阵，此时的BEKK-GARCH模型即改进为对角BEKK-GARCH(DBEKK-GARCH)模型，此时条件方差展开可得：

(14)

(15)

hsf,t=CssCsf+αssαffεsf,t-1+βssβffhsf,t-1

(16)

DBEKK-GARCH模型虽然能够减少待估参数个数，并满足条件方差-协方差矩阵的正定性，但参数的经济意义不明显，其变化对未来方差和相关系数不十分明确。

3.DCC-GARCH模型

Bollerslev提出CCC-GARCH模型。其假设不同资产收益率之间的相关系数是固定不变的，并简化了估计，从而使其在研究中得到广泛应用。但在实际应用中，一些金融序列的相关系数并不是固定不变的，因此Engle对CCC-GARCH模型进行扩展，假定不同的资产收益率之间的相关系数随时间动态变动，得到了DCC-GARCH模型：

与CCC-GARCH模型不同的是，条件相关系数矩阵是动态矩阵，在套期保值中，模型可展开为：

(17)

(18)

(19)

4.Copula-GARCH模型

Copula模型提出的比较早，1959年由Sklar提出，主要根据随机变量的边缘分布函数研究随机变量之间的相关关系。首先利用GARCH模型得到剔除ARCH效应的现货S和期货F的收益率的边缘分布情况，然后根据Copula理论，若在时间t时，股票现价收益率Rs为和股指期货合约收益率为Rf的联合分布函数Fs,f(x,y)各自的分布函数为Fs(x)和Ff(y)时,则必存在一个二元Copula函数C(u,v)，使得Fs,f(x,y)=C[Fs(x),Ff(y)]。本文在研究时主要是应用二元正态Copula函数和二元t分布Copula。

对于随机变量Rs,t-1、Rs,t-2，二元正态Copula函数分布为：

(20)

其中，Rf,t-1为相关系数，Rf,t-2为标准二元正态分布的联合分布函数，φ-1为一元标准正态分布函数的反函数。

对于随机变量X、Y，二元t分布的Copula函数表示为：

(21)

其中，ρ为相关系数，tρ,k表示相关系数为ρ、自由度为k的二元标准t分布的联合分布函数，t为服从自由度为C的标准Zt-1分布函数的反函数。

最后，在Copula-GARCH模型下，我们所要估算的最优套期保值比率为：

三、最优套期保值比率实证分析

(一)研究数据选取与描述

目前，我国市场上共有六支沪深300ETF，分别为华泰柏瑞沪深300ETF、嘉实300ETF、华夏沪深300ETF、南方开元沪深300ETF、易方达沪深300ETF、鹏华沪深300ETF。其中，易方达沪深300ETF、鹏华沪深300ETF、南方开元沪深300ETF上市较晚，偏短的样本周期将不能很好地展现价格运行规律；而华夏沪深300ETF交投不活跃，日均成交量仅为33.9万，实际操作中有一定的流动性风险。因此，我们拟从华泰柏瑞沪深300ETF与嘉实300ETF中选择一支对沪深300指数拟合最优的品种作为套期保值的现货标的。

我们主要从Pearson相关系数和跟踪误差的角度对二者进行研究。选取从2012年5月28日至2014年4月14日的日收盘价格数据。

ATE华泰=0.000118，ATE嘉实=0.000129

进一步验证华泰柏瑞沪深300ETF对沪深300指数的拟合情况更好，故将其作为本文研究的现货标的，期货标的选取沪深300股指期货的当月连续合约(IF00)。为消除序列的非平稳性，分别取期货和现货的日对数收益率为观测值，记作Rf、Rs。研究区间为2012年5月28日至2014年4月14日，其中2012年5月28日至2013年12月31日为样本内数据，2014年1月2日至2014年4月14日为样本外数据。

首先，我们对Rf、Rs样本内序列进行基本统计特征的描述(参见表1)。

表1 Rf与Rs的描述性统计分析

由表1可以看出，Rf与Rs的标准差比较接近，说明期货和现货的收益风险比较接近。JB 统计量、偏度和峰度值表明二者不服从正态分布，且具有金融时间序列共有的明显的尖峰、厚尾的特征；相关系数为0.9554，显示二者存在较强的相关性，可以进行套期保值。

对时间序列数据进行平稳性检验是进行时间序列回归的基本前提条件，为了防止伪回归，我们使用ADF检验方法验证Rf和Rs的平稳性，结果如表2所示。

表2 Rf和Rs的ADF检验结果

单位根检验的结果表明，二者在1%的显著性水平上均拒绝了原假设，表明期货和现货的收益率序列均为平稳的时间序列。

(二)最优套期保值比率估计

1.静态套期保值比率估计

(1)OLS模型估计。运用OLS模型，估计得到Rs=0.0000226+0.9236Rf。可知，最优套期保值比率h*=β=0.9236，对回归方程的残差进行进一步检验，结果显示，虽然方程的各方面统计值显示拟合状况良好，但金融时间序列的异方差等特性会给估计带来一定的风险，具体结果如表3所示。

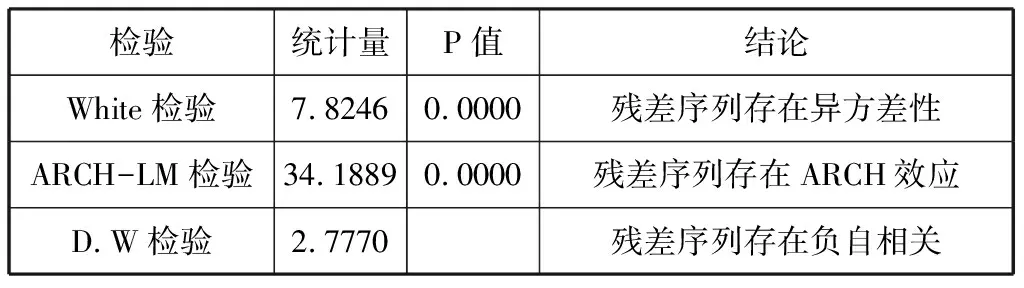
表3 残差检验结果

(2)B-VAR模型估计。运用AIC和SC准则确定VAR模型的最优滞后阶数为2，建立二元VAR(2)模型，参数估计结果如表4所示。

表4 B-VAR(2)模型的参数估计

注：*，**和***分别表示10% 、5%和l% 的显著性水平。

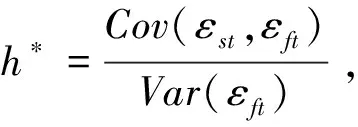
(3)VECM模型估计。由于Rf和Rs均为平稳序列，Pf与Ps之间可能存在协整关系。运用Johansen检验方法对变量进行协整检验，发现在5%的置信水平下，Pf与Ps之间存在且只存在一个协整关系，建立VECM(2)模型，估计如表5所示。

表5 VECM(2)模型的参数估计

注：*，**和***分别表示10% 、5%和l% 的显著性水平。

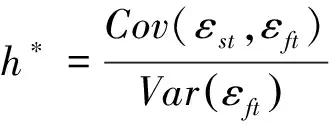
2.动态套期保值比率估计

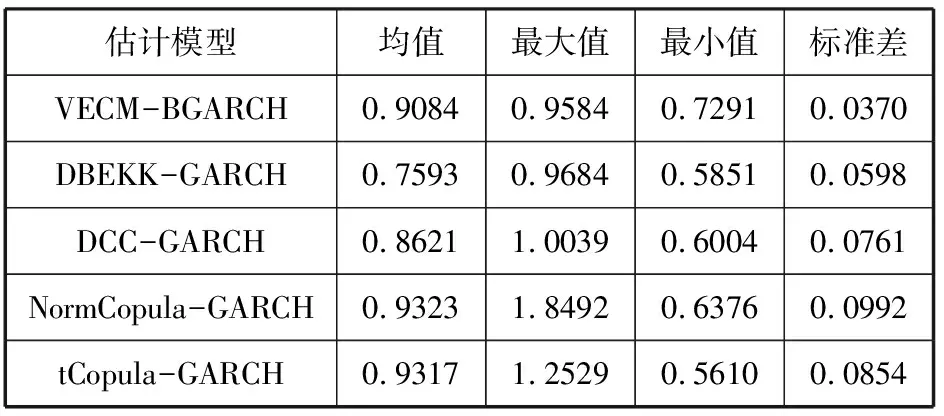
表6 动态最优套期保值比率

四、套期保值效率度量

可根据Ederington提出的风险评估指标HE来度量沪深300股指期货套期保值的效率。具体形式为：

(22)

下面，我们运用HE指标来度量沪深300股指期货套期保值效率，结果如表7所示。

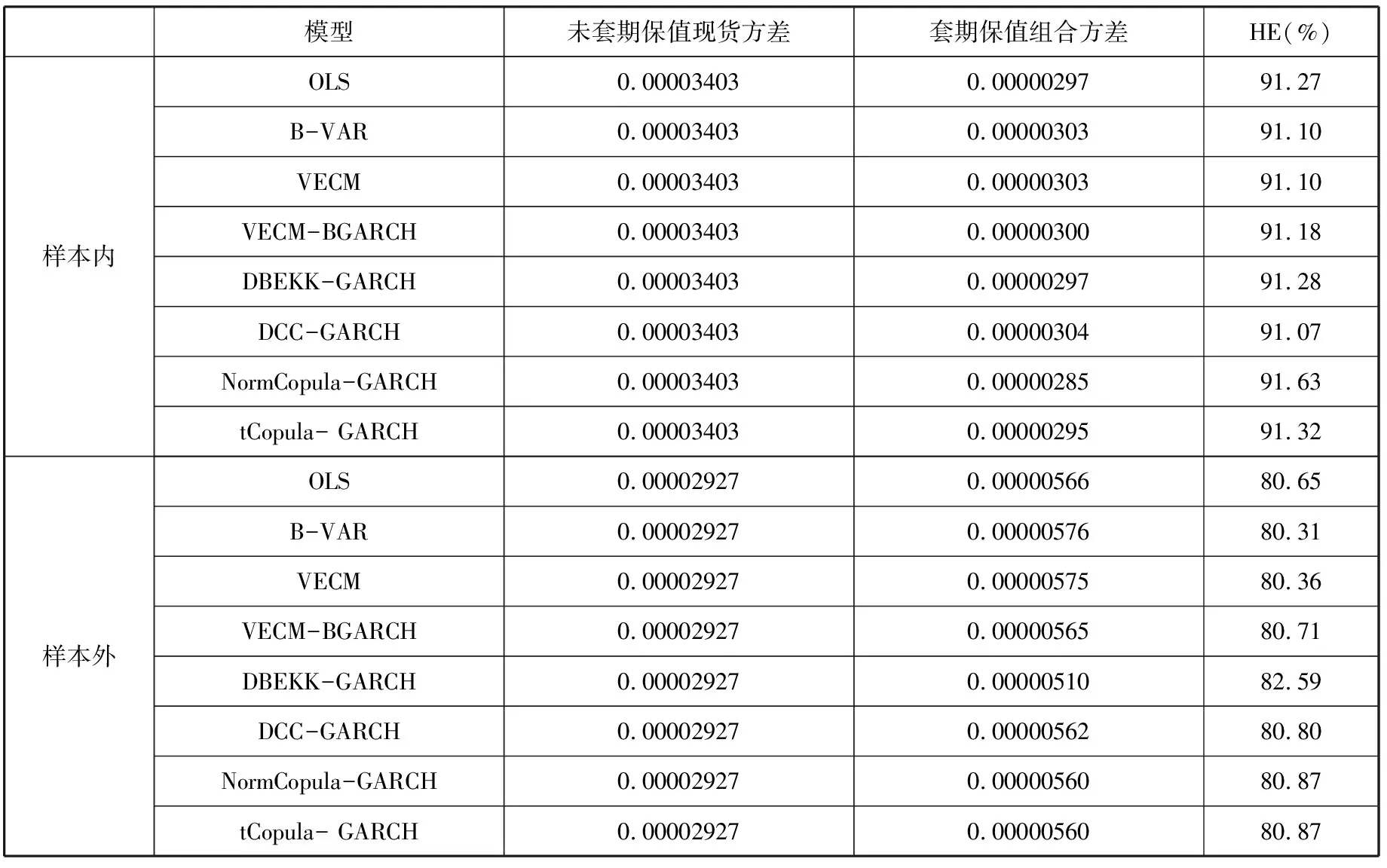
表7 套期保值效率度量结果

从表7可以看出，在样本期内各模型反映出的沪深300股指期货套期保值效率都比较高，均能够通过套期保值规避现货资产组合90%以上的风险。其中NormCopula-GARCH模型的效果最好，套期保值效率达到91.63%，其次是t分布的Copula-GARCH模型，套期保值效率为91.32%。在样本外数据分析中，同样是Copula-GARCH模型的效果最好，正态和t分布情况下的效率值都达到了80.87%。结果表明，股指期货市场与现货市场相关性较高时，股指期货能够高效发挥规避风险的功能。

从样本内套期保值效率度量结果来看，基于Copula-GARCH模型的套期保值策略对冲风险效果最好，而基于DCC-GARCH模型的套期保值策略效果相对较差，静态的最优套期保值比率估计模型也能够很好地对冲现货风险。

从样本外套期保值效率度量结果来看，基于动态最优套期保值比率估计模型的套期保值效果整体上优于静态最优套期保值比率估计模型，基于Copula-GARCH模型的套期保值策略仍然是最优的。这在一定程度上说明，由于市场环境的不断变化，我国股指期货与现货的相关系数可能也是不断变化的，因此需要对最优套期保值比率进行动态调整,从而提高套期保值效率。

五、结语

随着我国资本市场的发展，沪深300股指期货能够高效地发挥套期保值功能。研究表明，基于NormCopula-GARCH模型的套期保值操作相对于其他模型的效果最优，在理论上能够最大限度地对冲现货风险。但在实际应用中，该模型的套期保值比率是动态调整的，可能会造成调仓的成本较高。因此，还需从成本的角度综合考察静态与动态套期保值比率模型的套期保值效果，从而使沪深300股指期货充分发挥规避风险的作用。

参考文献：

[1]Herbst A F,Kate D,Caples S C.Hedging Effectiveness and Minimal risk Hedging Ratios in the presence of Autocorrelation:Foreign Currency Futures[J].Journal of Futures Markets,1989,9(3)：185-197.

[2]Myers R J,Thompson S R.Generalized optimal hedge ratio estimation[J].American Journal of Agricultural Economics, 1989,71(10)：858-868.

[3]Ghosh A.Hedging with stock index futures:estimation and forecasting with error correction model[J].The Journal of Futures Markets, 1993,13(7),743-752.

[4]Bera.A.,Gareia.P.and Roh.J.,Estimation of time-varying hedging ratios for Corns and soybeans:BGARCH and random coefficient approaches[J].Sankhva,1997,(59)：346-368.

[5]Yeh.S.C.and Gannon.G.L.,Comparing trading performance of the constant and dynamic hedge models: a note[J].Review of Quantitative Finance and Accounting,2000,(14)：155-160.

[6]Chih-Chiang Hsu,Chih-Ping Tseng,Yaw-Huei Wang.Dynamic hedging with futures:A copula-based GARCH model[J].Journal of Futures Markets，2008，28(11)：1095-1116.

[7]高辉，赵进文．沪深300股指套期保值及投资组合实证研究[J]．管理科学，2007,(4)：80-90．

[8]吴先智.股指期货的最优套期保值率实证研究——基于沪深300指数期货仿真交易视角[J]．上海立信会计学院学报，2008,(4)：78-84．

[9]陈守东，胡铮洋，孔繁利.Copula 函数度量风险价值的 Monte Carlo 模拟[J].吉林大学社会科学学报,2006,(3):85-91.

[10]朱志红，王向荣.股指期货套期保值的实证研究[J]．商业经济，2011,(22)：10-13.

[11]吴春来.沪深300股指期货套期保值比率研究[D].成都：西南财经大学，2012.

[12]蒋彧.基于GARCH-copula模型的股指期货动态套期保值比率研究[J].中央财经大学学报，2013，(5)：38-45.