基于多重分形理论的原油市场耦合关系研究
2014-03-22张德园王雪飞
张德园,王雪飞
(成都理工大学 商学院, 成都 610051)
长期以来,原油市场耦合关系的研究都是以有效市场假说为基础来展开的。然而,大量实证研究表明,原油市场之间的耦合关系并不简单遵循随机游走(Random Walk)过程,而是普遍呈现出长记忆性、多重分形等非线性特征[1]。如果仍然运用传统的有效市场假说理论来研究原油市场之间的耦合关系,势必与原油市场的实际不符。而多重分形理论打破了原有的线性研究范式,从动力学和几何学的角度来探讨金融市场之间的复杂非线性特征,更为全面、细致地描述了金融资产价格在不同时间标度上不同波动程度的详细信息[2,3],因而受到了国内外学者的高度关注[4-7]。
就多重分形耦合关系研究方法而言,主要有多重分形降趋交叉相关分析法(MF-X-DFA)、多重分形降趋移动平均交叉相关分析法(MF-X-DMA)以及多重分形高度交叉相关分析法(MF-HXA)等[8-10]。虽然这些方法能够描述原油市场之间的非线性耦合关系,但它们只能描述两个原油市场之间的非线性耦合关系,而不能刻画多个原油市场之间的非线性耦合关系。而原油市场是一个多市场相互联系、相互影响的综合体,如果只考察两个市场之间的非线性依赖关系,那么就很有可能会遗漏诸多重要信息[11],从而影响原油市场非线性依赖关系分析的准确性。可引入耦合消除趋势波动分析法(Coupling Detrended Fluctuation Analysis,CDFA)来研究多个原油市场之间的非线性耦合关系。
基于以上分析,本文以我国原油市场和国际主要原油市场的原油现货价格为研究对象,运用CDFA方法来研究国内外原油市场耦合关系的多重分形特征,以探究不同原油市场之间的非线性依赖关系及其潜在的动力学特征,从而为我国原油风险管理部门以及投资者在原油市场风险管理方面提供决策参考。
一、耦合关系的多重分形特征研究方法
(一)耦合消除趋势波动分析方法
Hedayatifar(2011)在Zhou(2008)提出的MF-X-DFA方法[8]的基础上,提出了CDFA方法[12],以研究多个同时发生的非平稳序列之间耦合关系的多重分形特征,从而为研究多个市场之间的非线性耦合关系提供了一种新方法。

(1)构造累积和序列:
i=1,2,…,N,j=1,2…,n
(1)
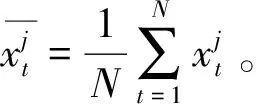

从头到尾进行分割
v=1,…,Ns
(2)
从尾到头进行分割
v=Ns+1,…,2Ns
(3)
(3)计算q阶波动函数

(4)
Fx1,…,xn(q,s)~shx1,…,xn(q)
(5)
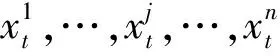
对于每一个s,求出对应的Fx1,…,xn(q,s)并通过双双对数图形即可求出耦合关系的广义Hurst指数hx1,…,xn(q),其关系式为:
lnFx1,…,xn(q,s)=hx1,…,xn(q)ln(s)+lnA
(6)
如果hx1,…,xn(q)>0.5,则表明n个收益率序列之间相应q值的耦合关系具有长期记忆性特征;如果hx1,…,xn(q)<0.5,则表明n个收益率序列之间相应q值的耦合关系具有反持久性特征;如果hx1,…,xn(q)=0.5,则表明n个收益率序列相应q值下不具有耦合关系或者是随机游走的。
当q>0时,hx1,…,xn(q)描述的是n个收益率序列在大波动中的标度行为;反之,当q<0时,hx1,…,xn(q)描述的是n个收益率序列在小波动中的标度行为。如果hx1,…,xn(q)随着q的变化而变化,则表明n个收益率序列之间的耦合关系具有多重分形特征;反之,如果hx1,…,xn(q)不随q的变化而变化,则表明n个收益率序列之间的耦合关系具有单重分形特征。
(5)根据Shardlkoo和Jafari的研究[13]可得多分形标度τx1,…,xn(q)和q之间的关系:
τx1,…,xn(q)=qhx1,…,xn(q)-1
(7)
结合勒让德变换(Legendre Transform),可得出多重分形谱参数:
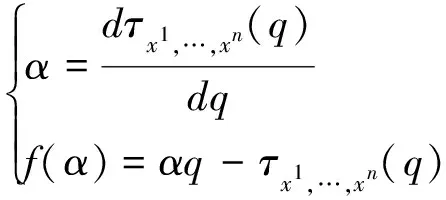
(8)
(二)耦合关系多重分形特征成因分析方法
一般来说,收益率序列多重分形特征主要有两个来源:(1)由大波动和小波动的长记忆性差异造成的;(2)由波动的厚尾概率分布引起的。通过对收益率序列进行随机重排(Random Rearrangement)处理,能够破坏收益率序列的长记忆性特征,而保留收益率序列的概率分布特征。相反,通过对收益率序列进行相位调整(Phase Adjustment)处理,能够弱化收益率序列的非高斯分布特征,而保留收益率序列的相关性特征。因此,通过对收益率序列进行随机重排处理和相位调整处理,能够有效地区分长记忆性和厚尾概率分布对收益率序列多重分形特征的贡献程度。
随机重排的主要步骤[14,15]为:(1)随机产生一组整数(p,q)。其中,p≤N,q≤N(N为收益率序列的长度);(2)对收益率序列中的第p个和第q个数据进行对换;(3)重复以上步骤20N次,以确保数据的位置被充分重置。
相位调整的主要步骤[16,17]为:(1)对收益率数据序列进行离散傅里叶变换(Discrete Fourier Transform);(2)将相位随机旋转一相位角;(3)进行傅里叶逆变换(Inverse Fourier Transform)。
如果经过随机重排或者相位调整处理后,时间序列的耦合关系呈现出单重分形特征,则表明收益率序列耦合关系的多重分形特征仅来源于收益率序列波动的长记忆性或者厚尾概率分布;如果经过随机重排和相位调整处理后,时间序列的耦合关系均呈现出弱化的多重分形特征,则表明收益率序列耦合关系的多重分形特征是由收益率序列波动的长记忆性和厚尾概率分布共同造成的。
(三)单一市场对耦合关系多重分形特征的影响度量方法
对于多个市场之间的耦合关系来说,其多重分形特征来源主要有收益率序列的长记忆性、厚尾概率分布以及长记忆性与厚尾概率分布三种情况。既然如此,那么在多个市场中,其耦合关系的多重分形特征主要是受哪一个市场的影响呢?据此,Hedayatifar等人提出了一种卡方统计量方法[12]来度量多个时间序列耦合关系中某一时间序列对整个时间序列耦合关系的影响程度,其统计量公式为:

(9)
σ(q)=
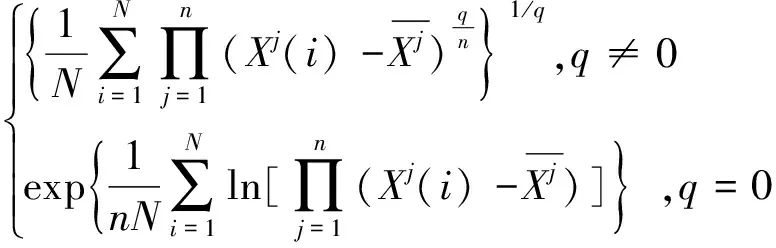
(10)

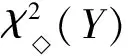
二、实证研究与分析
(一)样本选取与分析
本文选取美国西德克萨斯轻质原油现货价格(WTI)、英国北海布伦特原油现货价格(Brent)以及中东迪拜原油现货价格(Dubai)作为国际原油价格的代表,选取中国大庆原油现货价格(Daq)作为国内原油价格的代表,来研究国内外原油市场之间的非线性耦合关系。数据样本时间为2003年1月1日至2014年3月31日,剔除无交易以及日期不匹配的数据,总共得到2696组数据。数据来源于美国能源信息署(Energy Information Administration,EIA)和凤凰财经网。
通过公式rt=lnpt-lnpt-1(pt为第t日的收盘价)计算出各个市场的对数收益率序列并进行描述性统计与分析,其结果如表1所示。从表1中可以看出,所有收益率序列的均值均接近于0,偏度系数显著不为0,超额峰度均显著大于0,表明所有时间序列均具有有偏、尖峰特征,而J-B统计量结果也在1%的显著性水平下拒绝服从正态分布的假设;运用DFA计算出的Hurst指数值均大于0.5,表明所有收益率序列均不遵循随机游走的过程,而是呈现出长记忆性特征。

表1 原油市场收益率序列的描述性统计特征
注:***表示在1%的显著性水平下显著,Kurtosis为超额峰度;J-B统计量为Jarque-Bera统计量,DFA为Detrended Fluctuation Analysis计算出的Hurst指数。
(二)WTI、Brent、Dubai和Daq市场耦合关系检验
在运用CDFA方法分析WTI、Brent、Dubai和Daq四个市场之间耦合关系的多重分形特征之前,须对WTI、Brent、Dubai和Daq四个市场之间的耦合关系进行检验,以确定这四个市场之间是否存在耦合关系。图1为WTI、Brent、Dubai和Daq四个市场之间的耦合关系图。从图1中可以看到,四个市场之间的耦合关系统计量在5%的显著性水平下绝大多数都是显著的(绝大多数统计值都处在5%的边界线以内),表明WTI、Brent、Dubai和Daq四个市场之间存在着耦合关系。
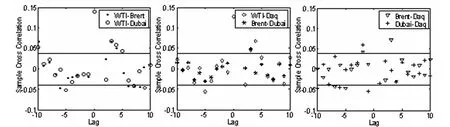
图1 WTI、Brent、Dubai和Daq四个市场耦合关系图
(三)原油市场耦合关系消除趋势波动分析
上文我们对WTI、Brent、Dubai和Daq四个市场之间的耦合关系进行了检验。然而,需要指出的是,上文的检验只是初步地表明了WTI、Brent、Dubai和Daq四个市场之间存在着耦合关系,而对于其耦合关系的特征以及程度等还需运用CDFA方法进行进一步分析。
根据公式(1)~(6),取n∈[10,N/5],q∈[-10,10]间的整数(N为收益率序列的长度),就可以得到WTI、Brent、Dubai和Daq四个市场之间非线性依赖关系的广义Hurst指数图,如图2(a)所示。从图2(a)中可以看出,四个市场耦合关系的广义Hurst指数均显著不为常数,而是依赖于q值的变化而变化,表明这四个市场之间的耦合关系具有多重分形的特征,而传统的线性模型以及单重分形模型并不能有效地反映原油市场之间复杂的非线性动力学特征。此外,还可以发现:当q<0时,h(q)显著大于0.5,表明小波动情况下的 WTI、Brent、Dubai和Daq市场耦合关系具有长记忆性特征,即某一市场价格的波动很有可能引起其他市场类似的波动;而当q>5时,h(q)近似于0.5,表明较大波动情况下的市场耦合关系很有可能是随机游走的。进一步,根据公式(7)和公式(8),可以得到WTI、Brent、Dubai和Daq市场之间耦合关系的多重分形标度指数τ(q)和多重分形奇异谱函数f(α),如图2(b)和图2(c)所示。由于τ(q)曲线的非线性程度反映了金融时间序列的多重分形强度,而图2(b)中的曲线为凸函数,进一步表明WTI、Brent、Dubai和Daq市场之间的耦合关系具有多重分形特征。图2(c)为四个市场之间的多重分形奇异谱函数,反映了金融系统复杂的动力学特征;而谱宽度Δα=αmax-αmin不仅反映了金融市场多重分形的强度,而且也衡量了金融市场波动的绝对大小。从图2中还可以看到,α值在0.3816至0.7424之间,谱宽度Δα为0.3608,表明WTI、Brent、Dubai和Daq市场之间的耦合关系具有多重分形特征,从而说明原油市场之间具有复杂的非线性依赖关系。
(四)原油市场耦合关系多重分形特征来源分析
正如上文所析,WTI、Brent、Dubai和Daq四个市场之间的耦合关系具有明显的多重分形特征。既然如此,那么这种多重分形特征是由什么造成的呢?下面我们将对WTI、Brent、Dubai和Daq四个市场的收益率序列分别进行随机重排和相位调整处理,并在此基础上运用CDFA方法来检验和比较四个市场收益率序列耦合关系的多重分形特征。
图3分别为WTI、Brent、Dubai和Daq四个市场的原始序列、随机重排序列和相位调整序列的耦合关系的广义Hutst指数、分形标度指数和奇异谱函数图。从图3(a)中可以看到,原始序列的Hurst指数值从0.6951递减到0.4727,随机重排序列的Hurst指数从0.5943递减为0.5054,而相位调整序列的Hurst指数从0.5250递减到0.4919,其变化幅度从0.2224分别减少为0.0889和0.0331,表明原始序列经过随机重排和相位调整处理后,其耦合关系的多重分形特征明显减弱。而图3(b)中原始序列耦合关系的标度指数曲线的凸性也明显大于随机重排和相位调整处理后序列耦合关系的标度指数曲线的凸性,表明随机重排和相位调整处理后序列耦合关系的多重分形程度小于原始序列耦合关系的多重分形程度。同样地,从图3(c)中也可以看到,原始序列耦合关系的多重分形谱宽度为0.3608,而随机重排和相位调整序列耦合关系的多重分形谱宽度分别为0.1702和0.087,表明原始序列经过随机重排和相位调整处理后,其耦合关系的多重分形程度明显减弱,并且相位调整处理后序列耦合关系的多分形谱宽度明显小于随机重排处理后序列耦合关系的多重分形谱宽度,说明厚尾概率分布对原油市场耦合关系多重分形特征的影响大于不同波动程度的长记忆性对耦合关系多重分形特征的影响。总之,WTI、Brent、Dubai和Daq四个市场之间的耦合关系具有明显的多重分形特征,而且这种多重分形特征是由厚尾概率分布和不同波动程度的长记忆性两者共同造成的,但厚尾概率分布对原油市场耦合关系多重分形特征的影响大于长记忆性对耦合关系多重分形特征的影响。
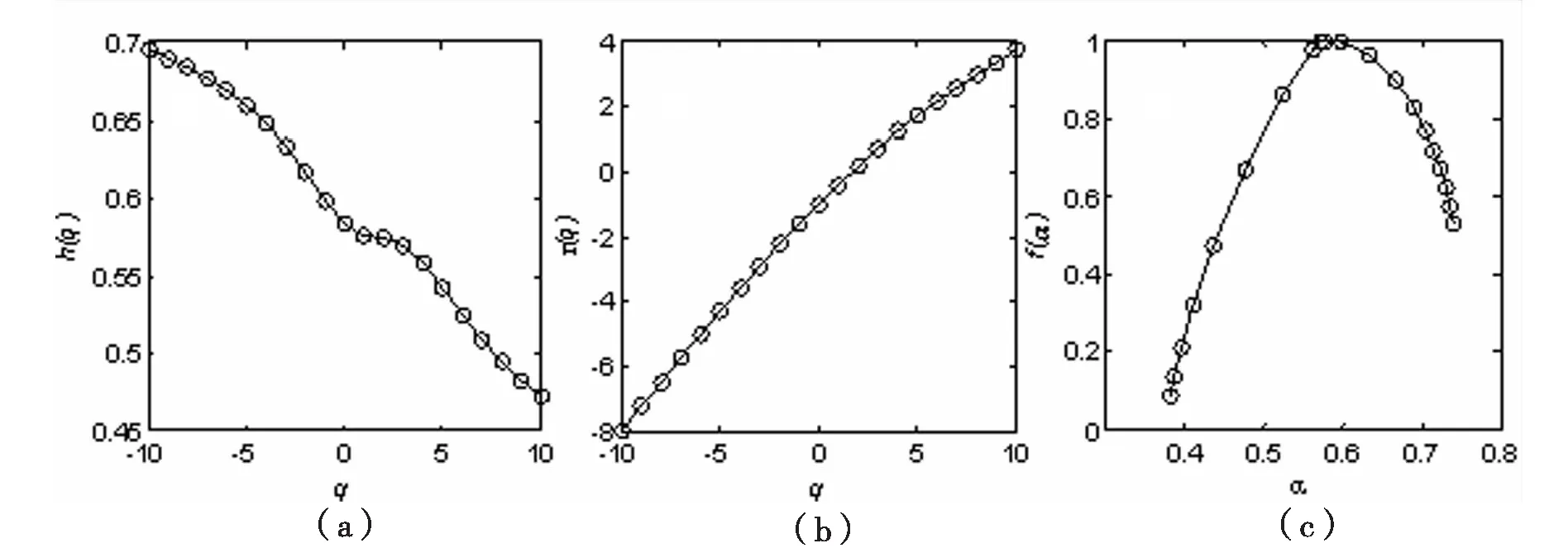
图2 四个市场耦合关系的广义Hurst指数、分形标度指数和奇异谱函数图
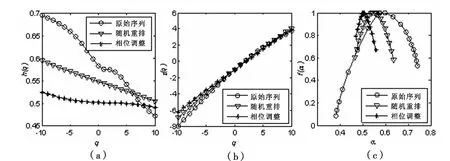
图3 原始序列、随机重排和相位调整后耦合关系的广义Hurst指数、标度指数和奇异谱函数图
(五)原油市场对耦合关系多重分形特征的影响分析
上文分析结果表明,WTI、Brent、Dubai和Daq四个市场之间耦合关系的多重分形特征是由波动的厚尾概率分布和不同波动程度的长记忆性两者共同造成的,那么在这四个原油市场中究竟哪一个市场的多重分形特征对原油市场耦合关系的多重分形特征具有较大的影响呢?下面我们将对单个原油市场对四个市场耦合关系多重分形特征的影响进行探讨与分析。
图4(a)为WTI、Brent、Dubai和Daq四个市场中某一市场经过随机重排处理后与其他三个市场原始序列耦合关系以及四个原始序列耦合关系的广义Hurst指数图(1)。从图4(a)中可以直观地看到,WTI、Brent和Daq曲线离CDFA曲线的距离较远,而Dubai曲线距CDFA曲线较近,表明就不同程度波动的长记忆性而言,WTI、Brent和Daq三个市场对原油市场耦合关系多重分形特征的贡献度较大,而Dubai的贡献度较小。同样地,图4(b)为WTI、Brent、Dubai和Daq四个市场中某一市场经过相位调整处理后与其他三个市场原始序列耦合关系以及四个原始序列耦合关系的广义Hurst指数图。从图4(b)可以看到,距离CDFA曲线最远的为WTI曲线和Dubai曲线,其次为Daq曲线和Brent曲线,表明就波动的厚尾概率分布来说,WTI和Dubai市场对原油市场耦合关系多重分形特征的影响程度较大,其次为Daq市场,而Brent市场影响程度最小。
然而需要说明的是,上面的分析只是直观地表明了各个原油市场对四个市场耦合关系多重分形特征的影响,而对于这种影响的量化还需运用严格的统计量方法进行分析。表2为单个原油市场对四个市场耦合关系多重分形特征的影响的统计量结果。从表2中可以看到,经过随机重排处理后,WTI市场的影响度为14.2832,Brent市场的影响度为4.0532,而Dubai和Daq市场的影响度分别为0.2798和0.8430。这表明就大小波动的长记忆性而言,对原油市场耦合关系多重分形特征影响较大的是WTI市场和Brent 两个市场;而经过相位调整处理后,WTI市场的影响度为15.1576,Brent市场的影响度为2.1351,而Dubai和Daq市场的影响度分别为7.1474和2.6249,表明就厚尾概率分布而言,对原油市场耦合关系多重分形特征影响较大的为WTI市场和Dubai市场,而其他市场影响较小;无论是经过随机重排处理,还是经过相位调整处理,WTI市场对原油市场耦合关系多重分形特征的影响均最为突出。因此,对于原油市场整个耦合关系而言,应重点关注WTI市场,其次是Dubai市场和Brent市场,最后是Daq市场。
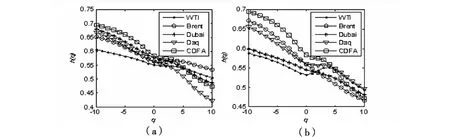
图4 某一序列随机重排和相位调整后耦合关系的广义Hurst指数

χ2◇(Y)WTI14.283215.1576Brent4.05322.1351Dubai0.27987.1474Daq0.84302.6249
三、结论
为准确反映国内外原油市场之间的非线性依赖关系及其潜在的动力学特征,本文引入耦合消除趋势波动分析法(Coupling Detrended Fluctuation Analysis,CDFA),以美国西德克萨斯轻质原油现货价格(WTI)、英国北海布伦特原油现货价格(Brent)、中东迪拜原油现货价格(Dubai)和中国大庆原油现货价格(Daq)为典型研究对象,实证分析国内外原油市场耦合关系的多重分形特征,并在此基础上进一步分析耦合关系多重分形特征的来源以及单个原油市场对耦合关系多重分形特征的影响,得出以下结论:
(1)原油市场之间的耦合关系具有明显的多重分形特征,表明原油市场是一个复杂的非线性系统,而传统的线性理论以及单重分形理论分析方法并不能有效反映原油市场之间复杂的非线性动力学特征。
(2)原油市场耦合关系的多重分形特征是由原油市场波动的长记忆性和厚尾概率分布共同造成的,但厚尾概率分布对原油市场耦合关系多重分形特征的影响大于长记忆性对耦合关系多重分形特征的影响。
(3)就大小波动的长记忆性而言,原油市场耦合关系多重分形特征主要是受WTI市场和Brent市场的影响;而就厚尾概率分布而言,原油市场耦合关系多重分形特征主要是受WTI市场和Dubai市场的影响;无论就长记忆性而言,还是就厚尾概率分布而言,WTI市场对原油市场耦合关系的多重分形特征的影响均最为突出。因此,对于我国原油投资者和原油风险管理部门而言,应重点关注WTI市场对我国原油市场价格的影响,同时也要关注Brent市场和Dubai市场对我国原油市场价格的影响,更有效防范和应对原油市场价格波动风险。
注释:
(1)图中曲线WTI是指WTI经过随机重排(图a)或者相位调整(图b)后与Brent、Dubai、Daq市场原始序列之间的耦合关系的广义Hurst指数曲线,其他曲线(Brent、Dubai、Daq)以此类推;CDFA曲线是指四个原油市场原始序列之间耦合关系的广义Hurst指数曲线。
参考文献:
[1]Wang Y D, Wei Y, Wu C F. Detrended fluctuation analysis on spot and futures markets of West Texas Intermediate crude oil [J]. Physica A, 2011,(390): 864-875.
[2]Mandelbrot B. A multifractal walk down Wall Street [J]. Scientific American, 1999, 280(2): 70-73.
[3]周孝华, 宋坤, 杨秀苔. 股票价格持续大幅波动前后多重分形谱的异常及分析[J]. 系统工程学报, 2006, 20(2): 92-96.
[4]Onali E, Goddard J. Are European equity markets efficient? New evidence from fractal analysis [J]. International Review of Financial Analysis, 2011,(20): 59-67.
[5]Engelen S, Norouzzadeh P, Dullaert W,etal. Multifractal features of spot rates in the liquid petroleum gas shipping market [J]. Energy Economics, 2011,(33): 88-98.
[6]Kristoufek L, Vosvrda M. Commodity futures and market efficiency [J]. Energy Economics, 2014,(42): 50-57.
[7]曲红涛, 庄新田, 田琨, 等. 我国螺纹钢线材市场的分形特征[J]. 系统管理学报, 2014, 23(2): 208-216.
[8]Zhou W X. Multifractal detrended cross-correlation analysis for two nonstationary signals [J]. Physical Review E, 2008, 77(6): 66-211.
[9]Jiang Z Q, Zhou W X. Multifractal derending moving average cross-correlation analysis [J]. Physical Review E, 2011, (84): 16-106.
[10]Kristoufek L. Multifractal height cross-correlation analysis: A new method for analyzing long-range cross-correlations [J]. Europhysics Letters, 2011, (95): 68001.
[11]王雪标, 周维利, 范庆珍. 我国原油价格与外国原油价格的波动溢出效应——基于DCC-MGARCH模型分析[J]. 数理统计与管理, 2012, 31(4): 571-584.
[12]Hedayatifar L, Vahabi M, Jafari G R. Copuling detrended fluctuation analysis for analyzing coupled nonstationary signals [J]. Physical Review E, 2011, (84): 21-138.
[13]Shadkhoo S, Jafari G R. Multifractal detrended cross-correlation analysis of temporal and spatial seismic data [J]. European Physical Journal B, 2009, 72(4): 679-683.
[14]Cao G X, Cao J, Xu L B. Asymmetric multifractal scaling behavior in the Chinese stock market: Based on asymmetric MF-DFA [J]. Physica A, 2013,(392): 797-807.
[15]许林, 宋光辉, 郭文伟. 基于滑动窗口MF-DFA的股票风格资产收益多重分形分析[J]. 系统工程理论与实践, 2012, 32(9): 1891-1899.
[16]黄健柏, 程慧, 郭尧琦, 等. 金属期货量价关系的多重分形特征研究——基于MF-DCCA方法[J]. 管理评论, 2013, 25(4): 77-85.
[17]Small M, Tse C K. Detecting determinism in time series: The method of surrogate data [J]. IEEE Transactions on Circuits and Systems, 2003, 50(5): 663-672.
