交通方式划分离散选择模型的比较研究

陈先龙

0 引 言

出行者交通方式选择行为特征是制定城市客运交通政策的先决条件之一。离散选择模型是研究出行者交通方式选择行为的基本方法，使用离散选择模型对出行选择的行为影响因素进行研究，研判城市客运出行方式结构，是城市交通规划决策的有效手段和重要基础。

运输市场中出行者会选择最适合自己的交通方式，同样的，交通工具也会“选择”最有能力的出行者。因此，出行者选择交通方式的过程中除了会受到交通工具属性的影响外，也会受到消费者本身的经济能力、偏好等内在因素（个人属性）的影响。由于交通方式选择行为描述、预测精度会受到各种不同变量的影响，因而选择一个恰当且解释能力强的离散选择模型是十分关键的问题。

国内外虽然有很多学者对离散选择模型进行了不同层次的研究[1-14]，但面对离散选择理论体系众多模型，如何从中选择合适的模型以有效解决交通方式选择行为预测问题仍然是困难的。有鉴于此，本研究针对交通方式选择行为建模预测问题，对五种典型的离散选择模型进行比较，研讨选择最佳离散选择模型的依据，并提出选择策略。

1 离散选择模型产生及MNL模型

离散选择理论起源于心理学与经济学，1980年代以来它已成为选择行为模型研究的基本手段，其核心为各选择枝的效用函数。常见的效用函数的数学模型表达式如下：

式中，njU 为方案j带给决策者n的效用；njV为可衡量效用；njε为误差项（不可衡量效用），nγ′为决策者n的参数向量，njZ 为观察到的变量；njx为决策者 n所具有的个体特性向量，njy为替选方案j所具有的特性向量。nN∈，N为决策者个体总量，jJ∈，J为可以选择的方案数量。

个体选择模型建模过程中假设消费者为理性的选择者，则个人n选择方案i的概率为：

式（2）中假定误差项njε满足独立一致同分布假设（Independent and identically distributed, I.I.D）并服从如下第I型极值分布：

式中，ηnj为位置参数；λ为离散参数。

此分布的方差为 π2/6λ2。令λ=l、ηnj=0，则得MNL(Multinomial Logit Model)的选择概率模型，这也是最简单的离散选择模型：

关于可衡量效用，一般多指定为参数的线性关系，亦即 Vni= βnxni+ α yni。 因此，个人 n选择方案 i的概率可表示如下：

将式（5）经过简单推导，可以得到式（6）。该数学式即为多项Logit模型的不相关替选方案独立（Independence from Irrelevant Alternatives, I.I.A）特性：

（6）式的意义为，在全部方案集合中，决策者对于任意两个替选方案选择概率比值，仅与该两替选方案效用有关，与其他替选方案之效用无关。

另一方面，如果假设个人n面对第i个方案作决策时不受其自身特性nix的影响，则上述多项 Logit模型（5）可以改写成下式：

式（7）即条件 Logit模型，此模型的特点在于其所有的决策只取决于选择方案所具有的特性(jy)，而与决策者特性(nX)无关。估计时等于假设每一组选择对于个人效用的影响都是相同的，所以不论有多少组选择方案，需估计的参数值只有一组。若研究中方案较多，则适合利用条件Logit模型来建模，同时也方便其他模型与之比较。

MNL模型在实际应用中需满足不相关替选方案独立（I.I.A）特性。I.I.A特性意味着方案之间彼此独立没有关连，且二替选方案选择概率的比值，仅与该两替选方案效用有关，与其他替选方案效用无关。I.I.A特性来自于误差项的I.I.D假设（误差项概率分布满足独立、相同的第I型极值分布）。若存在着异质性与相似性问题，则 I.I.D条件不能保证，进而导致错误统计推断。

除了I.I.A特性限制外，MNL模型应用时另外两个较大缺陷是：不能处理随机偏好差异；不能运用面板资料来从事未被观察到的有序列相关因素的研究。MNL模型的优点为：型式封闭；参数估计便利。

部分学者认为就模型理论而言，此特性是完全合理的。如 McFadden（1975）[15]就认为 I.I.A的限制虽然使得某些应用 MNL的研究失去价值，但是I.I.A所造成的偏误是来自研究对象而非理论本身。他认为在同质群体中，I.I.A 特性是成立的。Ben-Akiva（1985）[2]进一步指出，I.I.A虽然不适用于整个群体，但是I.I.A特性的确存在于同质群体，因此 I.I.A 特性的可信程度取决于模型考虑的群体异质性是否显著。若群体异质性不显著，则MNL 模型是最佳建模选择。但也有部分学者认为I.I.A 假设不适当且不适用于一般情况。基于以上分歧，众多学者在寻找其他更好的模型。

2 离散选择模型改进与发展

异质性与相似性问题与模型误差项假设有直接关系。影响误差项的因素有两个方面：观察样本与替选方案。因此可以从样本、替选方案两个角度来考察异质性与相似性问题。从样本的观点来看异质性，其代表着决策者的方式选择行为中对特定的交通方式有不同的看法，即个体间的品味有差异，或称为“个体异质性”。个体异质性主要来自偏好异质与回应异质，前者包含个体社会经济特性对于运输方式选择的可观察及不可观察的影响效果，后者则是个体对于运输方式服务水平的评价差异，同样存在可观察及不可观察的影响。

而所谓相似性，系指样本间调查获取过程中可能会因为空间或时间上的自相关（例如重复访问同一受访者或者抽样对象间的样本因区位相邻之因素可能造成数据间自相关等）而造成其存在相似性的问题(Bhat,1998)[16]。这两类难以完全避免的特性容易造成参数估计偏误甚至高估特定因素影响。

至于从替选方案的观点来考察异质性与相似性特性，则只需考核替选方案间是否满足 I.I.A之特性即可。若方案间不独立或不同质，则选择方案之间会有相似与异质的问题产生，亦即所谓的“方案相似性”与“方案异质性”。

近三十年来，为克服异质性与相似性问题，众多学者逐步发展出 NL(Nested logit model)模型、HEV(Heteroscedastic extreme value model)模型、MMNL(Mixed multinomial logit model)模型和MNP(Multinominal probit model)模型。

2.1 NL模型

NL模型引入巢层的概念，将具有相似性的替选方案放在同一巢层中。其假设同巢层内的替选方案的误差项为独立且相同的第I型极值分布，而属于不同巢层内的替选方案误差项则不相同。这里以两层巢式架构为例，假设模型中共M个巢，第m巢层中有Jm个方案且方案i为m巢层中方案之一，则方案i被决策者选中的概率为：

NL模型将具有相关性的替选方案置于同一独立巢层中，并利用包容值代表这些方案的共同效用，再与其他独立之替选方案构建模型，以达到各方案间相互独立的效果。故此NL模型优点在于适合于解决部分替选方案存在相似性的情况。其不足也很明显：一是须指定固定的巢层结构；二是无法处理所有随机误差项之间同时存在相关性的情况；三是需假定决策程序满足连续性条件；四是须限定每个替选方案只能出现在一个巢中。

2.2 HEV模型

HEV模型由 Bhat(2001)[17]提出。该模型允许替选方案njε满足独立不一致第I型极值分布，即各替选方案拥有各自的方差，可能相同也可能不同，而不同方案间的协方差则为零。个人n选择方案i的概率为

式中，Ψ (·)与 ψ (·)为第I型极值分布的累积分布函数与概率密度函数。C为选择集合，

w=εniθi，θi为替选方案的异质性参数，反应出不确定性因素的程度，也就是不确定性因素的权重，不同的替选方案对整体效用会有不同程度的影响。θi越大则可观测效用对选择概率的单位变动量将趋缓。

HEV模型通过各替选方案误差项的方差表达式中引入尺度因子而允许替选方案误差项的方差不同（各自的方差可相同也可能不同），且不同方案间的协方差为零。HEV模型仅能处理方案间存在异质性的问题，若方案间同时存在相似性问题，则使用该模型将会造成大偏差。

2.3 MNP模型

Daganzo(1979)[18]提出若式（2）中，假设随机误差项服从正态分布，则可推导得到MNP模型。MNP模型允许随机误差项间彼此可以不完全独立且不相同，能充分表现出决策者的实际选择行为，为最一般化模型。MNP模型的数学表达式为：

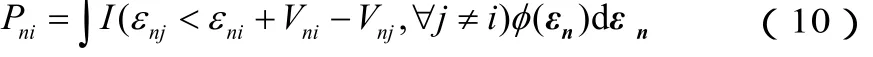
式中， I (·)为指标函数， I(·)=1则表示决策者选择了其中效用最大者，否则为0；φ(εn)为多元正态分布，，期望E ( εn) = 0，Ω为协方差矩阵。

模型（10）带有复杂的积分项，当选择集合超过四个方案时，参数求解较困难。

MNP模型则不会受到上述 MNL模型的三种限制，其可以处理异方差问题，可设定任何型式的误差结构，亦可运用面板数据处理时间序列相关的误差项。MNP模式唯一的限制是必须假设效用函数所有的误差项均为正态分布。大部分的情况下，假设随机项为正态分布是适当的，但某些情况下，假设为正态分布并不适合，且会导致违反常理的预测结果，最著名的例子就是价格变量的系数，应采用密度分布只出现在大于 0的一侧的分布，如对数正态分布较为合理，但此种分布无法纳入MNP模型中。除了此项限制之外，MNP模型参数求解较复杂。

2.4 MMNL模型

MMNL 模型假定决策者的偏好应该不同，因此假设边际效用服从某种分布，使得须对MNL模型的参数积分得到 MMNL的概率。决策者n选择方案 i的概率表示如下：

式中，Lni(γ)是在特定参数向量下的多项Logit选择概率：

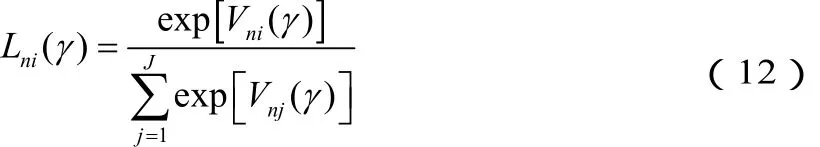
而 g (γ)=g(γ θ)是概率密度函数，θ是深层参数向量，包括均值、方差或协方差等； Vni(γ)是可衡量效用。

如果将效用指定为线性组合，亦即 Vni( γ) = γ'Zni，则MMNL的选择概率可表示如下：

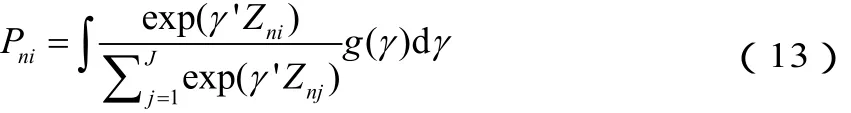
MMNL模型的选择概率取决于γ的分布形态。常见的分布形态是均匀分布、三角分布、正态分布、对数正态分布。在实证研究中 g (γ)究竟为何种分布，须由研究者探索之后认定。现有多数研究，如Hensher和 Greene（2002）[19]等均设定 g (γ)服从正态分布或对数正态分布。

MMNL模型的效用函数中除了可观测部分的非随机项以及误差项外，还包括不可观测部分的随机项。而透过此随机项可考虑方案间的相关性、异质性以及个体偏好异质性。MMNL可同时处理异质性与相似性问题，因此理论上MMNL模型假设最接近真实情况，其对于偏好行为解释效果最佳。

若MMNL模型中效用设定为线性组合，则MNL为MMNL模型的特例。MMNL模型的优点在于：允许个体之间存在偏好差异性；可用来刻划同一消费者不同出行间的相关性；可逼近任何其他随机效用模型的估计结果。MMNL模型的缺点是计算过程繁杂，需要高速计算机估计参数；参数的分布未知需要特别制定，可能产生问题。

有必要说明的是，MNL、NL、HEV、MMNL、MNP模型参数估计方法不完全相同。MNL、NL、HEV模型参数一般采用极大似然法辨识得到。MMNL、MNP模型未知参数估计则必须采用极大模拟似然法。

以误差项假设独立与一致的二维观点解析离散选择模型，可将本文介绍的五种模型作如下分类，见表1。

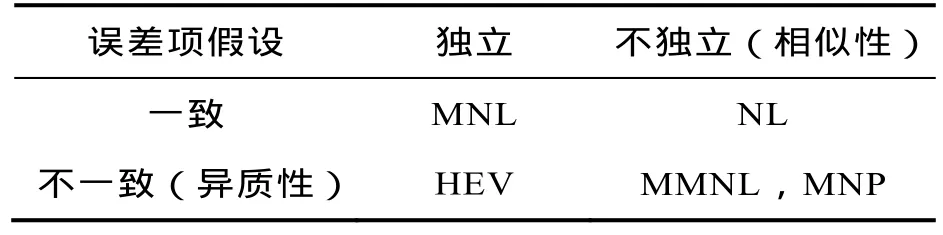
表1 离散选择模型的分类Tab.1 Discrete choice models’ classification

由上述分析可知，每种模型均有优缺点，若将其很好组合应用则在实践中可能得到满意结果。

3 算 例

这里使用悉尼与墨尔本之间的通勤出行者问卷调查数据[20]来对五种离散选择模型进行研究。原数据源于对 210个通勤出行者从悉尼到墨尔本面对小汽车、火车、长途公共汽车、飞机四种交通方式的选择行为调查，主要变量如下：①T——站点等待时间，小汽车交通方式为0（min）；②S——车内时间（min）；③G——广义成本，等于车辆成本＋车内时间×时间价值；④H——家庭收入。

待估计的效用函数表达式为：

对于任意j，εij服从相同的独立分布，即Ⅰ型极值分布， Fε(εij) = e xp(− e xp(− εij))，其标准偏差为 π2/6。di,m是选择交通方式i时交通方式m的二元变量。αm是交通方式m二元选择变量的参数。 di,f是选择交通方式i时航空交通方式的二元变量。

首先以小汽车出行方式为参照方案，建立 MNL模型，采用极大似然法估计参数可得全集合、受限制集合情况下的参数值（见表2）。（受限制集合是指剔除航空方式的集合）。

表 2数据是采用小汽车作为标准参照组计算得到的。由结算结果可知，因豪斯曼检验值HM=33.3363大于 χ02.05=9.488，说明模型 I.I.A 假设未通过检验，即意味着存在异质性与相似性的问题，需要建立其他模型研究选择行为。

表2 MNL模型校估结果Tab.2 Result of MNL calibration

计算表明火车、公共汽车和小汽车均可作为标准参照组，但航空不能作为标准参照组，因它会导致参数不可辨识。

这里采用图 1的树状 NL模型作为例子估计参数。

图1 NL模型结构Fig.1 Nested logit model structure

检验NL模型估计结果可得到10.945＞20.05χ=5.99，即拒绝I.I.A假设。从计算结果可知NL模型较之MNL模型能提高选择行为的解释能力。

方案之间可能存在异质性，这里尝试将一尺度因子加入各替选方案的误差项中，使得各替选方案的误差项不再均等，而存有方案异质性的问题。在HEV模型中，需要至少固定一方案的尺度因子才可以估计其他参数的尺度因子，为了便于模型比较，此处假设小汽车为基础方案，且其尺度参数值为1。其他参数的尺度因子估计值为：航空=0.2485，火车=0.2595，公共汽车=0.6065。Bhat的实证研究发现，HEV模式的解释能力比NL模型及MNL模型好。本例计算结果表明（见表 3）HEV模型对选择行为的解释能力强于MNL模型但劣于NL模型。

MNP模型参数估计中固定小汽车参数值为0，得出的一组结果见表3。MNP模型对选择行为的解释能力并未增强，可能与假设有关，即某些效用函数的误差项并不是正态分布。

表3 NL模型、HEV模型与MNP模型校估结果Tab.3 Model calibration results of NL,HEV and MNP

以前述全集合状态下的MNL模型为基本型建立 MMNL模型。采用极大似然模拟估计方法得到参数见表4，分为独立随机参数与相关随机参数两种情况。研究采用 Halton序列并将抽样数设定为125。

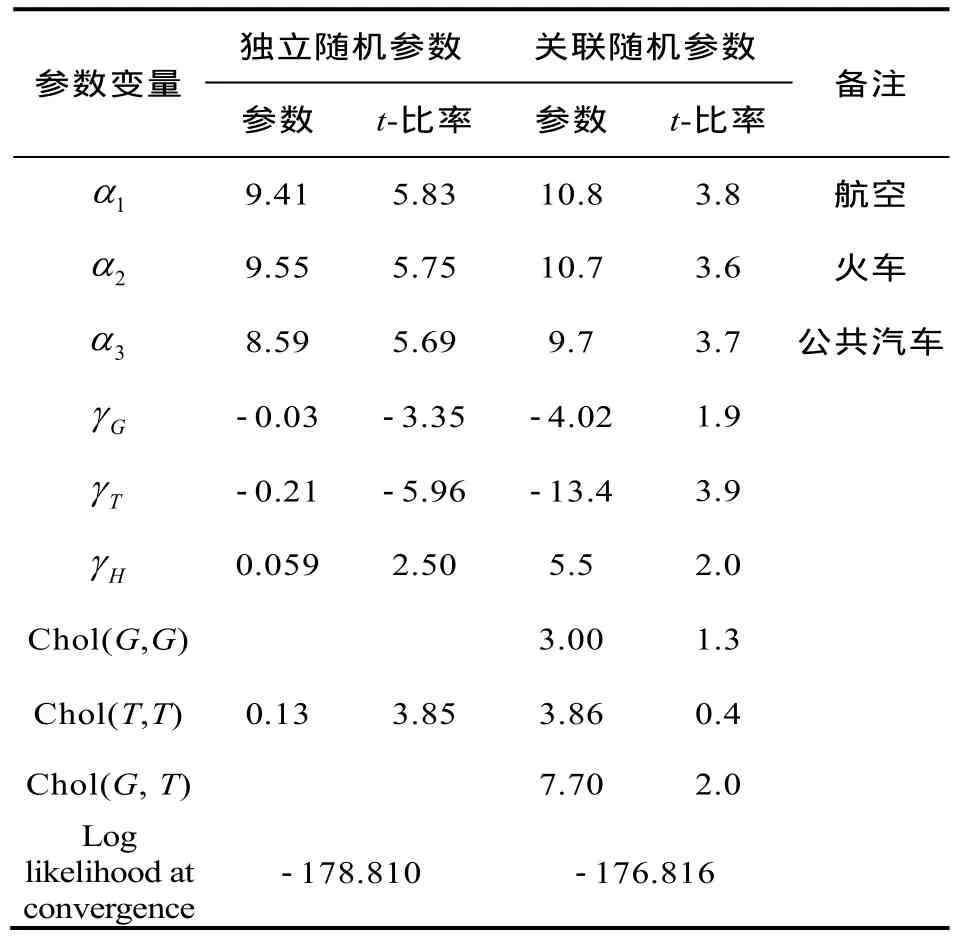
表4 MMNL模型校估结果Tab.4 Model calibration result of MMNL

总体而言，在本文所有模型中MMNL 模型解释能力最好。

4 结束语

本文对常见离散选择模型进行了比较研究，重点介绍它们各自的理论基础并比较了它们的差异。通过算例研究得出一些具有价值的结论：

（1）与其他模型相比，MMNL模型可以大幅度提升模型解释度，但应用中依然有参数分布不可随意设定的缺陷。若能正确选择参数的分布，该模型应是最优选择。

（2）MNP模型必须设定效用函数所有的误差项为正态分布的原生缺陷，导致实践中MNP模型解释能力可能不强。

（3）NL模型应用上需先确定决策者的行为架构，若决策程序无法确知，将使得选择结构建立十分困难，而决策结构建立若有重大错误，对于模型结果影响甚大。此外，决策者的决策程序为连续性假设有时可能与事实不符。

[1] Train K. Discrete choice methods with simulation(2nd ed)[M]. Cambridge∶ Cambridge University Press, 2009∶ 388.

[2] Ben-Akiva M. E., Lerman S. R.. Discrete choice analysis ∶ theory and application to travel demand[M].Cambridge Mass.∶ MIT Press, 1985∶ 390.

[3] Lerman S. R. Discrete choice analysistheory and application to travel demand[M]. Cambridge Mass∶MIT Press, 1985∶ 390.

[4] Hensher D. A., Swait J. D., Louviere J. J. Stated choice methods ∶ analysis and applications[M].Cambridge UK∶ Cambridge University Press, 2000∶402.

[5] Greene W.H., Hensher D A. A latent class model for discrete choice analysis∶ contrasts with mixed logit[J].Transportation Research Part B∶ Methodological.2003, 37(8)∶ 681-698.

[6] Antoniou C., Matsoukis E., Roussi P. A Methodology for the Estimation of Value-of-Time Using State-of-the-Art Econometric Models[J]. Journal of Public Transportation, 2007, 10(3).

[7] Bhat C. R., Sidharthan R. A new approach to specify and estimate non-normally mixed multinomial probit models[J]. Transportation Research Part B∶Methodological, 2012, 46(7)∶ 817-833.

[8] Fosgerau M., Bierlaire M. A practical test for the choice of mixing distribution in discrete choice models[J]. Transportation Research Part B∶Methodological, 2007, 41(7)∶ 784-794.

[9] Bhat C. R., Castelar S. A unified mixed logit framework for modeling revealed and stated preferences∶ formulation and application to congestion pricing analysis in the San Francisco Bay area[J]. Transportation Research Part B∶Methodological, 2002, 36(7)∶ 593-616.

[10] Munger D., Ecuyer P. L., Bastin F, et al. Estimation of the mixed logit likelihood function by randomized quasi-Monte Carlo[J]. Transportation Research Part B∶Methodological, 2012, 46(2)∶ 305-320.

[11] Hess S., Bierlaire M. Polak J.. Estimation of value of travel-time savings using Mixed Logit models[J].Transportation Research Part A∶ Policy and Practice,2005, 39(3)∶ 221-236.

[12] Walker J., Ben-Akiva M. Generalized random utility model[J]. Mathematical Social Sciences, 2002, 43(3)∶303-343.

[13] 吴至中. 检视住宅选择行为中的异质性与相似性[D]. 台南∶ 国立成功大学, 2005.

[14] 鲜于建川. 通勤者活动—— 出行选择行为研究[D].上海∶ 上海交通大学, 2009.

[15] Mcfadden D., Domencich T. A. Urban travel demand ∶a behavioral analysis ∶ a Charles River Associates research study[M]. Amsterdam∶ North-Holland Pub.. Co., 1975∶ 215.

[16] Bhat C. R. Accommodating flexible substitution patterns in multi-dimensional choice modeling∶formulation and application to travel mode and departure time choice[J]. Transportation Research Part B∶ Methodological, 1998, 32(7)∶ 455-466.

[17] Bhat C. R.. Quasi-random maximum simulated likelihood estimation of the mixed multinomial logit model[J]. Transportation Research Part B∶Methodological, 2001, 35(7)∶ 677-693.

[18] Daganzo C. F. Multinomial Probit∶ The Theory and Its Application to Demand Forecasting[M]. New York∶Academic Press, 1979∶ 216.

[19] Hensher D. A, Greene W H. The Mixed Logit Model∶The State of Practice [R]. Sydney, 2002.

[20] Greene W. H. NLOGIT Version 5 Reference Guide[M]. New York∶ 2012∶ 650.