磁浮系统中免疫专家PID控制器的改进

宋荣荣 陈滋利

0 引 言

磁浮系统本身具有非线性和不稳定性特点，这增加了系统的控制难度和复杂度，系统容易出现安全隐患。尤其是当电磁铁垂直向上跟踪阶跃信号时，系统的超调量过大而撞击甚至吸死轨道，造成磁浮列车安全方面的严重后果[1]。目前的控制算法大多是采用以悬浮间隙作为位置信号并结合电磁铁的加速度和线圈的电流等信号进行传统的 PID控制[2,3]。然而，由于控制系统和参数的固定，传统的PID控制器无法完全兼顾系统的静态和动态性能，即无法获得最佳的控制效果。目前，很多国内外专家学者采用复合PID控制器提高磁浮系统的控制性能[4-10]。

在众多的控制器中，专家PID控制器是近年来发展起来的一种新型控制器[4-6]。其原理是不受被控系统精确模型的影响，而根据受控对象的特点和控制规律的效果，以专家的经验来制定控制规则在线调整PID参数，形成专家PID控制器。文献[4]结合了常规PID控制器和专家控制器的优点，在保留常规PID精度高的基础上，可以实现小超调或无超调控制器，并且，基于专家经验使控制器系统具有接近于人类操作经验的控制性能；文献[5]在惯性、时滞、数学模型不确定的情况下，基于PID闭环系统的阶跃响应曲线分析受控系统稳定的内在原因，制定了专家模糊控制规则，减少了超调量，缩短了延迟时间，从而提高了系统的控制性能；文献[6]结合了嵌入式系统高效、实时的控制性能和专家-模糊自适应控制器的快、稳、准的控制效果，提出了一种嵌入式专家-模糊PID控制器，验证了该控制器与单一的专家PID控制器和模糊PID控制器相比具有适用性较好、超调量较小、稳定速度较快的优点。但是，文献中并未提及如何获得专家 PID控制器中的参数和如何正确分辨专家规则中的不同误差变化情况。这将是本文要解决的主要问题。现将专家PID控制器、免疫PID控制器和粒子群优化算法结合起来，扬长避短，设计一种复合的PID控制器。这种复合型控制器既具有专家控制器的智能性，免疫控制器的适应性，PSO算法的优化速度快等特点，又具有PID控制器精度高的特点。因此，该控制器对磁浮系统具有良好的控制效果，这也是近年来十分热门的研究课题[7-10]。

本文主要研究中低速磁浮系统的控制器改进问题。先建立磁浮系统的数学模型，然后利用分段的思想，设计基于PSO算法的分段免疫专家-PID复合型控制器。其主要过程是以误差和误差变化率作为输入，利用免疫PID控制器得到的系统阶跃响应曲线，根据误差变化情况划分为五个不同阶段，利用专家控制器和PSO算法对不同阶段的PID参数进行自调整。最后，基于 Matlab软件的仿真结果表明该复合控制器与单一的专家 PID控制器相比对阶跃响应具有更好的跟踪效果。

1 磁浮系统的数学模型

假设电磁铁不仅在垂直方向运动，还沿轨道以速度V运行，磁浮系统结构如图1所示。

图1 磁浮系统的结构Fig.1 Structure of the magnetic suspension system

图1 中，绝对气隙 z ( t)为磁极表面与绝对参考平面的距离； h ( t)为轨道面与绝对参考平面的距离；相对气隙 c ( t)为磁极表面与轨道面的气隙。加速度计所测得的输出为加速度˙z˙(t)；气隙传感器测得的输出为相对气隙 c ( t)； i( t )为电流互感器测得的控制线圈电流； u ( t)为绕组回路的电压。

设N为电磁铁线圈的匝数，A为磁极面积，R为线圈的电阻，μ0为空气磁导率，mg为电磁铁重力，F( i, c)为悬浮电磁力， fd(t)为外界干扰力。

在分析单电磁铁悬浮系统的动力学模型时，假设[9]：

①忽略漏磁的影响；

②忽略磁铁芯和导轨中的磁阻，磁势均匀降落在气隙 c ( t)上。

③电磁铁仅有垂直方向上的移动，其他方向受限无运动。

根据电磁学和动力学理论，得到基于绝对参考平面的单电磁铁动态模型方程：

式中，平衡点的边界条件为：

在平衡点(i0, c0)附近进行线性化处理，可以得到状态方程：

令Δu( t)和fd(t)均为零，通过拉氏变换可分别得到相当气隙和绝对气隙与轨道变化的开环传递函数。

磁浮系统的开环传递函数为：

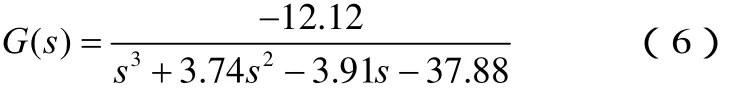
由系统的极点判定知[12]，这是一个三阶不稳定系统，为使电磁铁稳定悬浮必须采取反馈控制。

2 基于PSO算法的分段免疫专家PID控制器的设计

现将专家PID控制器、免疫PID控制器和PSO优化算法结合起来，扬长避短，设计一种复合PID控制器。这种EI-PID-PSO复合型控制器既具有专家控制器的智能性，免疫控制器的适应性，PSO算法优化速度快等的特点，又具有PID控制器精度高的特点，其控制器结构图如图2所示。

图2 PIEPID-PSO控制器结构Fig.2 The controller structure of PIEPID-PSO

2.1 分段免疫PID控制器设计

免疫 PID控制器的原理是借鉴生物系统的免疫机理而设计出的一种非线性控制器。生物体的免疫系统对外界侵入的抗原产生抗体，通过吞噬作用或特殊酶的作用而毁坏抗原[13]。

基于免疫原理提出如下假设：若第k代的抗原数量为ε(k)，则辅助细胞TH的数量为TH(k)=k1ε（k），k1为正的激励因子。将抑制细胞 TS的数量作为反馈控制，即 TS( k ) = k2f( S( k ) ,Δ S ( k ))，其中 k2为正的抑制因子， f(·)是一个非线性函数，表示抑制细胞的抑制量，输出范围为[0,1]， S ( k ) = TH(k ) − TS( k )是免疫反馈控制器，表示B细胞的总刺激。

反馈控制器规律如式（7）所示：

式中， ()e k为误差e的第k个值； ()u k为第k次控制器的输出， ( 1)u k− 为第 1k−次控制器的输出；kp、ki和kd分别为 PID控制器的比例、积分和微分系数；，K为控制反应速度，η 为控制稳定效果，f(·)为一个选定的非线性函数，表示细胞抑制刺激能力的大小。

2.2 专家PID控制器设计

令 ()e k表示离散化的当前采样时刻的误差值，( 1)e k− 、( 2)e k− 分别表示前一个和前两个采样时刻的误差，则有

根据误差及误差变化，令 M1，M2为设定的误差界限，M1＞M2，可设计专家规则如下：

1）当e( k)＞M1时，即误差变化很大。此时无论误差变化趋势怎样，控制器都按最大(或最小)输出，以达到迅速调整误差，使误差绝对值以最大速度减少。

2）当 e( k)Δ e( k)≥ 0时，即误差朝增大方向变化或误差没变化。当e( k)＞M2时，即误差较大，此时，控制器可实施较强的控制作用，以达到扭转误差朝减小方向变化，并迅速减小误差的绝对值，控制器输出为：

式中， k1为增益放大系数， k1＞ 1 。反之，当e( k ) ＜M2时，即尽管误差朝增大方向变化，但误差本身并不很大，此时，控制器可实施一般的控制作用，只要扭转误差的变化趋势，使误差朝减少方向变化即可，其控制器输出为：

3）当 e( k)Δ e( k) ＞ 0，或者e( k)=0时，即误差朝减少的方向变化或已经达到平衡状态。此时，控制器可保持输出不变。

4）当 e( k)Δ e( k) ＜ 0时，即误差处于极值状态。当e( k)≥M2时，控制器可实施较强的控制作用：

5） 当e( k)＜δ时，说明误差很小，此时加入积分，减少稳态误差。其中，δ为任意小的正实数。

《教育信息化2.0行动计划》提出,2022年基本实现“三全两高一大”的发展目标。其中，“一大”指建成“互联网+教育”大平台,推动从教育专用资源向教育大资源转变。教育信息化从1.0时代进入2.0时代[1]。教育信息化2.0将更注重经济地从广泛可获取的、大容量的、不同结构和类型的数据中获取教育价值。其突出优势就是分析事物注重“量化证据”，不仅仅揭示因果关系，而且揭示相关关系。同时，数据也是实现“人本”、“生态”、“智能”三要素协同发展的前提[2]。随着智能手机、平板等设备的兴起，移动学习愈发得到研究者的关注和重视。

2.3 基于PSO算法的PID控制器参数整定

上述免疫 PID控制器实际上是一个非线性的 P控制器，它可以在线整定PID控制器的参数，但是，由于存在非线性项，解析参数的值比较困难，因此需要利用优化方法求出参数的值。目前的寻优方法很多，例如单纯形法、专家整定法和遗传算法等。虽然这些方法都具有良好的寻优特性，但是，单纯形法对初值比较敏感，容易陷入局部最优解，造成全局寻优的失败；专家整定法需要大量的专家经验，整理经验需要大量的计算时间；遗传算法需要交叉、变异操作，因此，需要调整的参数过多。而粒子群 PSO算法保留了基于种群的全局搜索机制，更适合于全局优化，算法更简单，更易于实现[15]。

假设种群P中的粒子数为S，每个粒子的位置矢量由PID控制器的三个控制参数组成，即粒子位置矢量的维 3D=。该种群用矩阵表示为：

具体步骤如下：

（1）初始化 设定PSO算法中涉及的各类参数:搜索空间的下限 Ld和上限 Ud，学习因子 c1和 c2，算法最大迭代次数 Tmax或收敛精度ξ，粒子速度范围[vmin,vmax]；随机初始化搜索点的位置 xi及其速度 vi，设当前位置为每个粒子的位置 pi，从个体极值找出全局极值，记录该最好值的粒子序号q及其位置 pq。

（2）评价每一个粒子 设粒子i在t时刻的速度和位置为

为了获取满意的过渡过程动态特性和避免超调，采用了惩罚控制，即一旦产生超调，将超调量作为最优指标的一项，选择适应度函数为:

式中，e( t) ＜ 0 ，w3为权值，且 w4＞＞w1。通常w1= 0 .999，w2= 0 .001， w3= 2 ,w4= 1 00。

计算粒子的适应值，如果好于该粒子当前的个体极值，则将 pi设置为该粒子的位置，且更新个体极值。如果某个粒子的个体极值好于当前的全局极值，则将pq设置为该粒子的位置，且更新全局极值及其序号q。

（3）粒子的状态更新 粒子在 t + 1时刻的速度和位置分别为

式中，1≤i≤M，1≤ d ≤ D ，r1、r2为均匀分布在(0,1)区间的随机数，w为惯性权重，其表达式为

它的大小决定了粒子对当前速度继承的多少，选择一个合适的w，有助于 PSO均衡它的探索能力与开发能力。

如果 vi＞vmax，则将vi设置为vmax；如果vi＜vmin，则将 vi设置为 vmin。

（4）检验是否符合结束条件 如果当前的迭代次数达到了预先设定的最大次数 Tmax或最终结果小于预定收敛精度ξ要求，则停止迭代，输出最优解，否则转到步骤（2）。

在这种控制方法中，PSO算法首先进行离线学习，然后再接入到控制系统中。基于PSO算法的PID参数优化整定算法关键问题是：如何解决参数的编码及适应度函数的选择。

根据上述优化过程，可以对不同误差变化下求得预整定值： k′p， kI′， kD′，则不同阶段的PID控制器参数为 kp= k ′p+Δkp， ki= ki′+Δki， kd= kd′ +Δkd。

3 Matlab仿真分析

计算机仿真软件采用Matlab中的M函数进行仿真[16]，验证PIEPID-PSO控制器的性能。采样时间为1ms，采样点为1000个。磁浮系统的参数、免疫PID控制器的参数和PSO算法的参数如表1、表2和表3所示：

表1 悬浮系统的参数Tab.1 Parameters of the maglev transportation system

表2 免疫控制器的参数Tab.2 Parameters of the immune controller

表3 PSO优化算法的参数Tab.3 Parameters of PSO scheme

将单一的免疫 PID控制器仿真的阶跃响应曲线划分为 5个误差变化阶段，利用 PSO算法设置PID控制器参数，将参数代入专家PID控制器进行输出，对单一的免疫PID控制器和基于PSO算法的分段免疫专家PID控制器的仿真效果进行比较。

根据误差和误差变化率的5种情况，对单一的免疫PID控制器后的阶跃响应划分为五个阶段。分阶段图如图3所示。

结合PID参数的性质、专家控制规则和PSO优化参数算法对系统实际情况作出以下分析：

图3 单一免疫PID控制器的阶跃响应曲线Fig.3 Step response of single immune PID controller

1）a~b段，即悬浮系统处于快速跟踪信号状态，此时误差会很大，相当于系统处于e( k)＞M1阶段，控制器按最大输出，使误差以最大速度减少，因此，为避免系统响应出现较大超调，应增加 kp，减少 kd，限制 ki。此时，利用PSO算法预整定PID参数。

2）b~c段，此时 e( k)Δ e( k)＜0，即误差的绝对值朝减小的方向变化，系统较慢接近预定值，为抑制超调，应减小 kp，增大 ki和 kd。此时，利用PSO算法预整定PID参数。

3）c~d段，此时 e( k)Δ e( k)＞0，即系统处于超调状态，将到达偏离预定的最远位置。根据误差的大小可以对系统实施强弱不同的控制方式，即误差偏大时选取较大 kp；反之，选取较小的 kp，同时应该增加 kd，减小 ki。此时，利用PSO算法预整定PID参数。

4）d~e段，此时 e( k)Δ e( k)＜0，e( k)Δe( k−1)＞0，即系统由最远位置又回到预定位置。根据误差变化，应保持 kp，减少 kd，增大 ki。此时，利用PSO算法预整定PID参数。

5）e~f段，e( k)＜ε，即系统处于稳定状态，系统已经没有静差或静差已经小到允许范围内，并且对响应曲线已经满意。只需要比例和积分调节器提高系统抗干扰能力和系统的稳态精度。此时，利用 PSO算法预整定PID参数。

下面，利用PSO算法将上面5个不同阶段的PID参数预整定结果如表4所示：

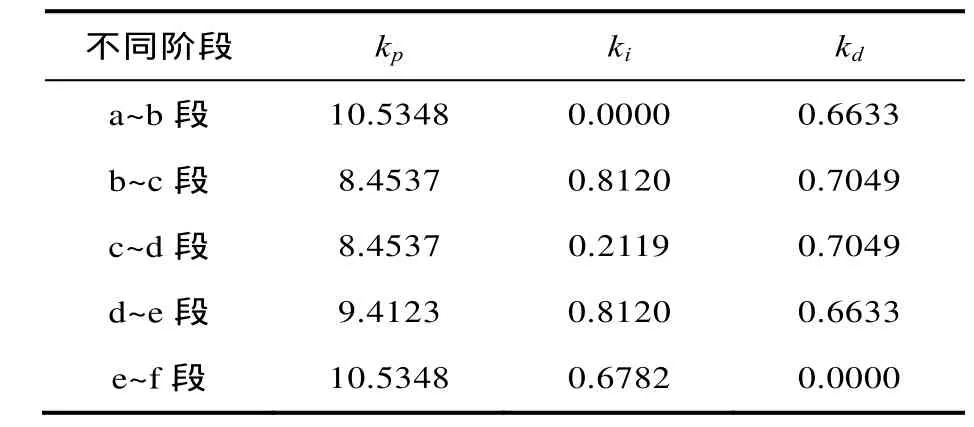
表4 5个不同阶段的PID控制器整定参数Tab 4 The tuning parameters of the 5 different stages of the PID controller

运行Matlab程序，PIEPID-PSO的系统阶跃响应曲线如图4所示。

图4 PIEPID-PSO控制器的阶跃响应曲线Fig.4 The step response of PIEPID-PSO controller

两种控制器的仿真结果如表5所示：

表5 PIEPID-PSO控制器和IPID控制器的时域分析Tab.5 The time domain analysis of PIEPID-PSO and IPID controller

5 结 论

本文先建立三阶悬浮系统，然后，利用免疫PID控制器给出系统的阶跃响应曲线并划分为 5个不同阶段，根据不同阶段的误差变化，利用专家控制规则和PSO算法在线调整PID控制器的参数。最后，基于Matlab中的M函数形式进行跟踪研究，结果表明:

（1）基于PSO算法的分段免疫专家PID控制器比单一的免疫 PID 控制器提高了悬浮系统的调节时间，减少了超调量，加快了系统的动态响应速度。从而，在系统精度相同的情况下，该控制器使悬浮系统调节精度提高，稳态性能变好，几乎没有超调和振荡，具有较强的鲁棒性。

（2）分段思想为控制器分析误差的不同变化提供了准确、快速而有效的帮助。这在实际悬浮系统控制器中有着重大的意义。

（3）一个理论必须在实践中得到成功的应用才能推动其不断完善和向前发展，专家控制器理论也是一样，今后将考虑如何将其和其它智能控制器结合，更好地应用到磁悬浮控制器中去，这是我们孜孜探求理论的最终目的。

[1] 龙鑫林, 佘龙华, 常文森. 电磁永磁混合型EMS磁悬浮非线性控制算法研究[J]. 铁道学报, 2011,33(9): 36-39.

[2] Wai Rong-Jong, Lee Jeng-Dao, Chuang Kun-Lun.Real-time PID control straegy for maglev transportation system via particle swarm optimization[J]. Industrial Electronics, 2011, 58(2): 629-646.

[3] Moazen M., Sharifian M. B. B., Afshari H. PID control of maglev guiding system for linear elevator[C].2012 IEEE 5thIndia International Conference on Power Electronics(IICPE), Delhi, India, 2012: 1-6.

[4] 龙 飞. 专家式PID调节器的设计与实现[J]. 科技传播, 2012, (5): 212-214.

[5] 杨 平. 污水处理中溶解氧专家模糊控制系统的研究[J]. 沙洲职业工学院学报, 2012, 15(1): 13-18.

[6] 洪 炎, 苏静明, 唐超礼, 张友能. 基于专家-模糊PID的冻结凿井智能流量控制研究[J]. 计算机工程与科学, 2012, 34(7): 166-171.

[7] Liu Tongjuan, Ma Xiangguo, Jin Nengqiang. Expert PID control study of hybrid maglev systems[C].ICMA 2009 International Conference on Mechatronics and Automation, Changchun, China, 2009: 876-880.

[8] Hong Yan, Su Jing-ming, Tang Chao-li, Zhang Vou-neng. Research on brine flux control based on fuzzy immune PID algorithm in freezing station[C].2012 IEEE International Conference on Computer Science and Automation Engineering (CSAE),Zhangjiajie, Hunan, China, 2012: 55-59.

[9] Varshney Sarika, Srivastava L., Pandit M.Comparison of PSO models for optimal placement and sizing of statcom[C]. Sustainable Energy and International Conference on Intelligent Systems(SEISCON2011), Chennai, India, 2011: 346-351.

[10] Sharifah Lailee Syed Abdullah, Hussin N.M., Harun H., Khalid N.E.A. Comparative study of randon-PSO and Linear-PSO algorithms[C]. 2012 International Conference on Computer Information Science (ICCIS),Kuala Lumpeu, 2012: 409-413.

[11] 谢云德, 常文森. 电磁型(EMS)磁悬浮列车系统铅垂方向的建模与仿真[J]. 铁道学报,1996，(4):47-54.

[12] 郑大钟. 线性系统理论[M]. 北京: 清华大学出版社, 2002:238-241.

[13] 刘 韬. 人工免疫系统及其数据挖掘应用研究[M].徐州: 中国矿业大学出版社, 2010: 38-56.

[14] 陶永华. 新型PID控制及其应用[M]. 北京: 机械工业出版社, 1998: 1-5.

[15] 李 丽, 牛 奔. 粒子群优化算法[M]. 北京: 冶金工业出版社, 2009: 25-32.

[16] 张智星. Matlab程序设计与应用[M]. 北京: 清华大学出版社, 2002: 360-365.