基于CCD非接触线径测量系统的设计与研究
2014-03-21熊静琪王李立
韩 星,刘 倩,熊静琪,王李立
(1.电子科技大学机械电子工程学院,四川成都 611731;2.北华航天工业学院电子工程学院,河北廊坊 065000)
0 引言
在电缆、光缆的生产中,直径的偏差直接影响着它们的等级.而目前线材外径的检测主要依靠人工的接触的检测手段。因而,检测速度低、劳动强度大,并且无法检测生产线上高速运动的线材外径[1]。激光检测技术能满足高速非接触在线检测的需要,而随着非接触测量技术的迅猛发展,线阵CCD因其响应速度快、信号易处理、精度高和无磨损的特点而广泛应用于一维尺寸测量中[2]。为此,采用半导体激光器,结合先进的快速光电耦合器件(CCD)以及计算机技术,研制出了能用于生产实际的高精度激光检测系统[3-4]。文中系统利用高速AD转换芯片对线阵CCD的信号进行AD转换,并由FPGA对转换的信号进行高速采集、存储和处理,最后将测量结果发送PC上位机[2]。
1 线径测量系统
线径测量系统由以下3部分组成:(1)光电系统;(2)单片机系统;(3)上位机系统。其系统组成如图1所示[3]。

图1 系统组成
1.1测径系统模型
激光束将被测量棒投影于CCD上,由于CCD是一个理想的光传感器,有很高的感光灵敏度,所以它在检测中成为一个高灵敏度的光电传感器件。又由于线阵CCD的光敏元阵列依靠高精度的光刻技术,有着精确的几何间距,所以,CCD在光电检测中又是一把数字式的高精度测量标尺[5]。当CCD的整个光敏元件阵列被激光照射时,在驱动脉冲作用下,其输出端将得到与CCD位数相应的脉冲信号数。当被测量棒被扇形激光束投影于CCD上时,部分CCD光敏元件将被遮去,仅在被光均匀照明的光敏元区域有对应位数的脉冲信号输出[6]。实际系统抽象出来的几何模型如图2所示。
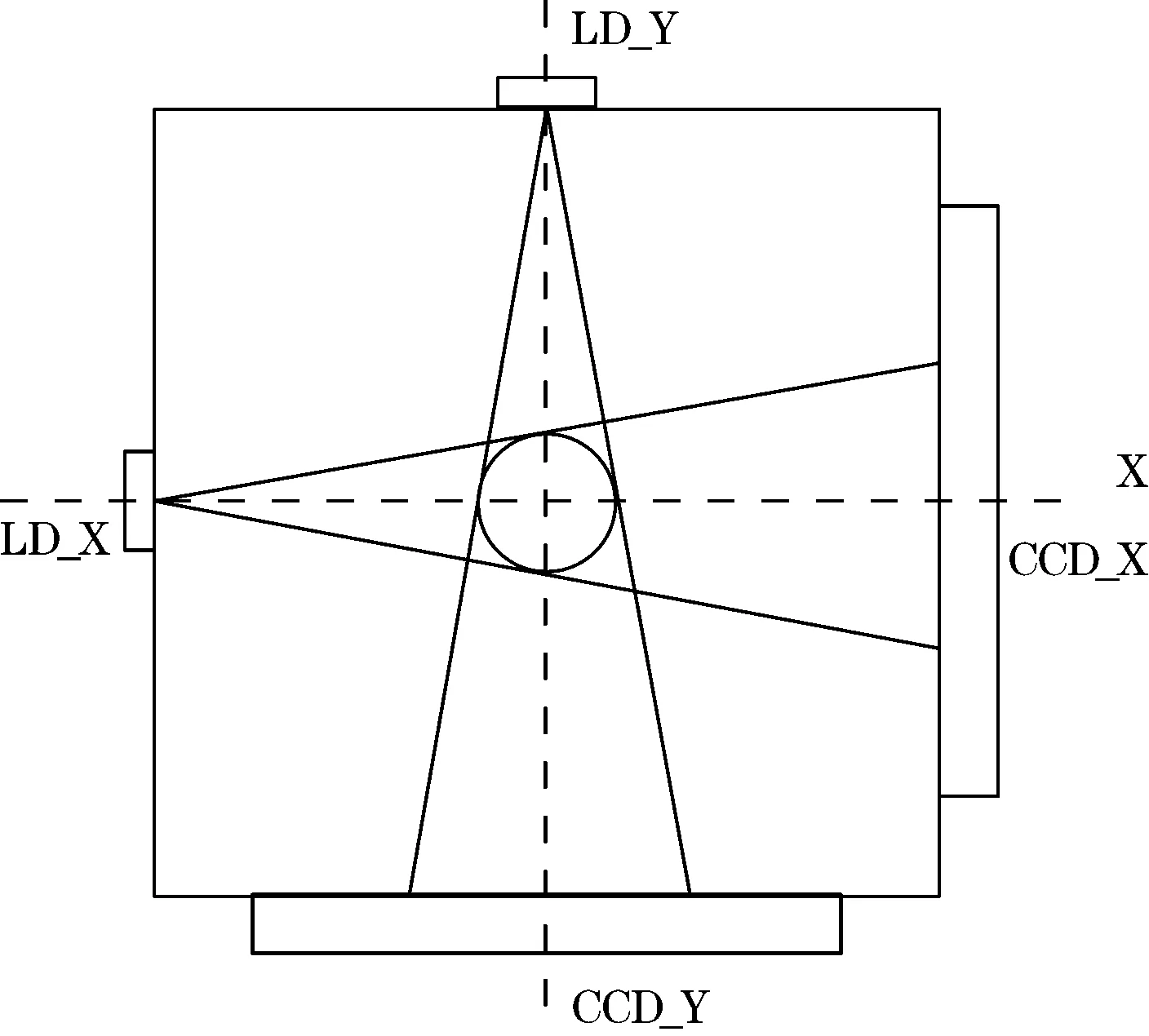
图2 光学模型
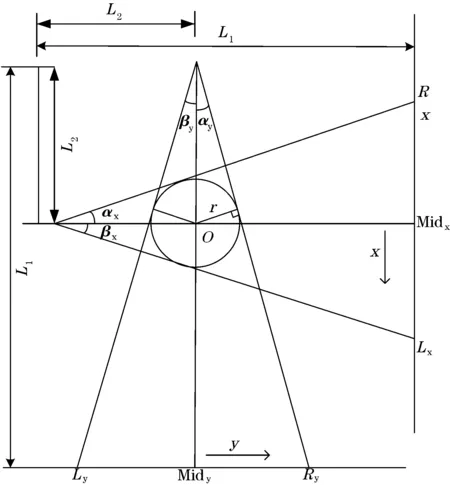
图3 光学几何模型抽象
1.2单片机系统电路设计
针对系统需求,系统选用STM32F103芯片作为主控芯片实现控制,其主要特点是:128 K字节的闪存程序存储器,20 K字节的SRAM;2个12位模数转换器,1 us转换时间(多达16个输入通道);七通道DMA控制器等[7]。
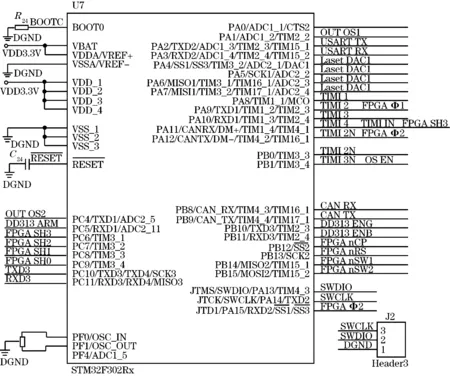
图4 单片机电路
1.3CCD驱动电路设计
CCD是检测系统的核心,其性能优劣直接影响系统的功能和检测精度,通常线阵CCD传感器,可靠性、灵敏度、分辨率等方面都能满足一般工业要求。根据系统需求情况,在考虑性价比、工作频率及使用简单等因素。TCD1209DG,它是一种高灵敏度、低暗电流的线阵CCD传感器。具有2 048位有效象元的两相阵线CCD器件,每个光敏元尺寸为14 μm×14 μm,中心间距14 μm.TCD1209DG为双列22脚封装,只需加上一组时序脉冲进行驱动控制就能实现对线径像的一维扫描和信号输出,硬件电路上通过增加一个驱动器SN72LVC1G66来实现。
TCD1209DG工作需要SH、Φ1、Φ2、RS 4路脉冲驱动。由非门及晶体振荡器构成的振荡电路输出频率为2 MHz的方波脉冲,经D触发器分频得到频率为1 MHz的方波脉冲,将2 MHz与1MHz脉冲相与形成RS脉冲,其占空比为1∶3,频率为1 MHz.将RS经D触发器分频产生频率为10 MHz的Φ1脉冲和Φ2脉冲,Φ1和Φ2反相。将SH、Φ1、Φ2、RS经反相器、阻容加速电路送至SN72LVC1G66驱动器,供给TCD1209DG[8]。驱动电路如图5所示。
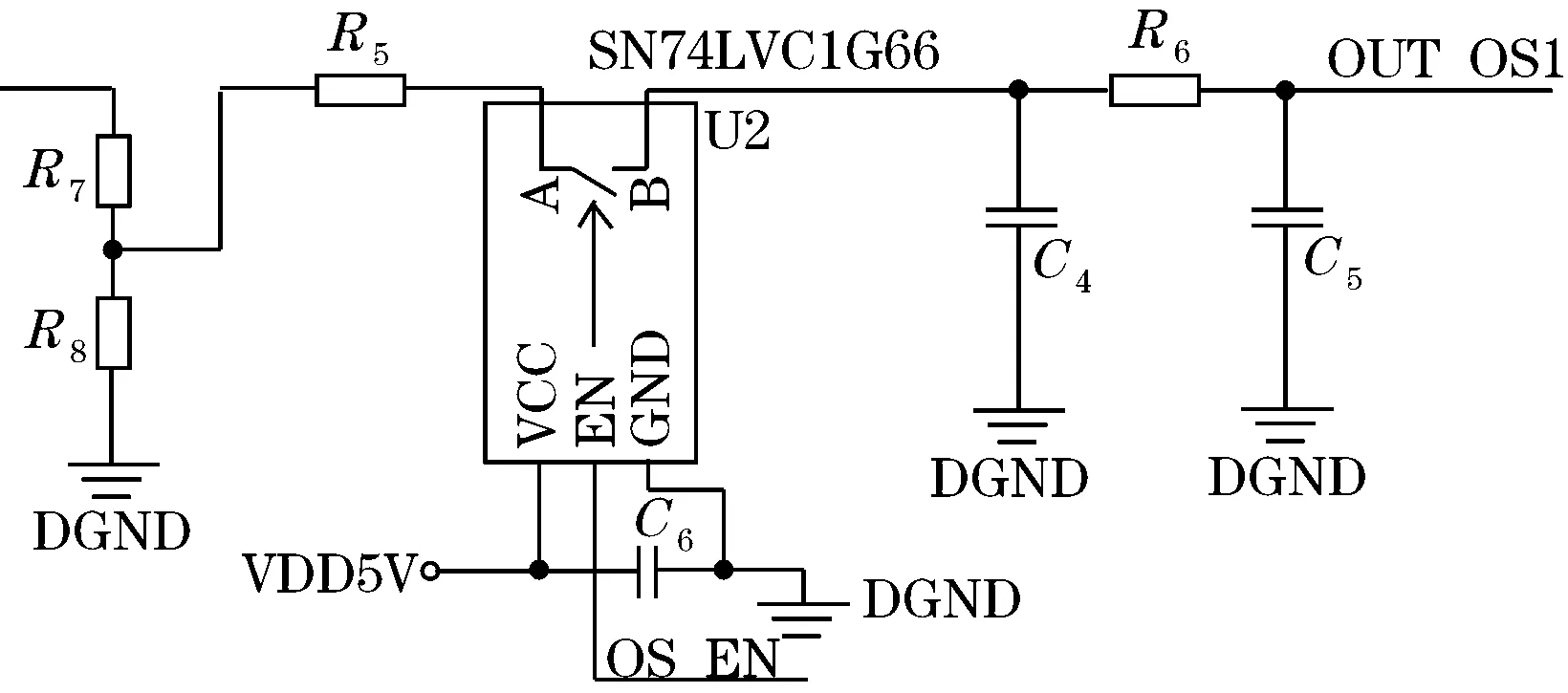
图5 CCD驱动电路
2 基于CCD几何模型算法
分析图3光学几何模型抽象,不难发现当量棒线径发生变化时,其几何模型相应的发生改变,这种改变最终直接导致了最终结果的误差,因此对几何模型做如图6所示修正。
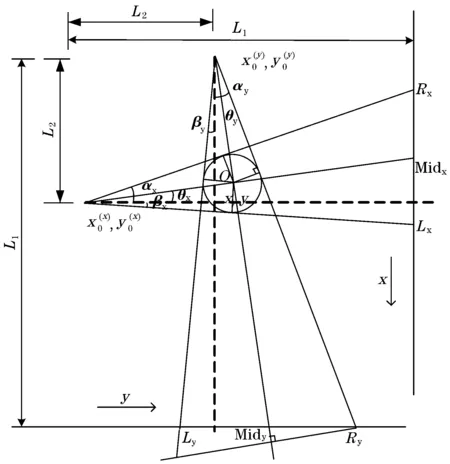
图6 改进后的光学几何模型
图中,可以判定两虚线焦点处为坐标原点,则得到实际中量棒的坐标(x,y),激光LD的坐标(0,-L2)(-L2,0),同时可以利用CCD测得衍射阴影坐标,Ly(L1-L2,ly),Ry(L1-L2,ry),Lx(lx,L1-L2),Rx(rx,L1-L2),其中L1为激光LD到CCD的距离。
利用三角关系,可以求得:
(1)
(2)
同时,由于测得衍射阴影坐标,可以解出sinαx,sinαy。同时两条垂直平分线斜率为:
(3)
(4)
同时利用αx,αy,kx,ky根据各条线之间的关系,可以得出其他两条曲线的斜率:
(5)
(6)
同理y方向有:
(7)
(8)
而根据坐标,可以确定以上4条曲线的斜率为:
(9)
(10)
联立以上方程,化简有:
(11)
(12)
(13)
(14)
由CCD测得Rx,Ry,Lx,Ly4个已知量,联立式(11)、式(12)、式(13)、式(14)最终可以求出量棒坐标(x,y),x方向线径x_width,y方向线径y_withy,综合二者得结果为:
(15)
3 实验仿真
3.1线径测量试验台
因系统对光污染比较敏感,因此在搭建系统时添加了遮光板,搭建的试验台如图7所示。图7黑色部分即是对CCD做出的相应遮光处理。
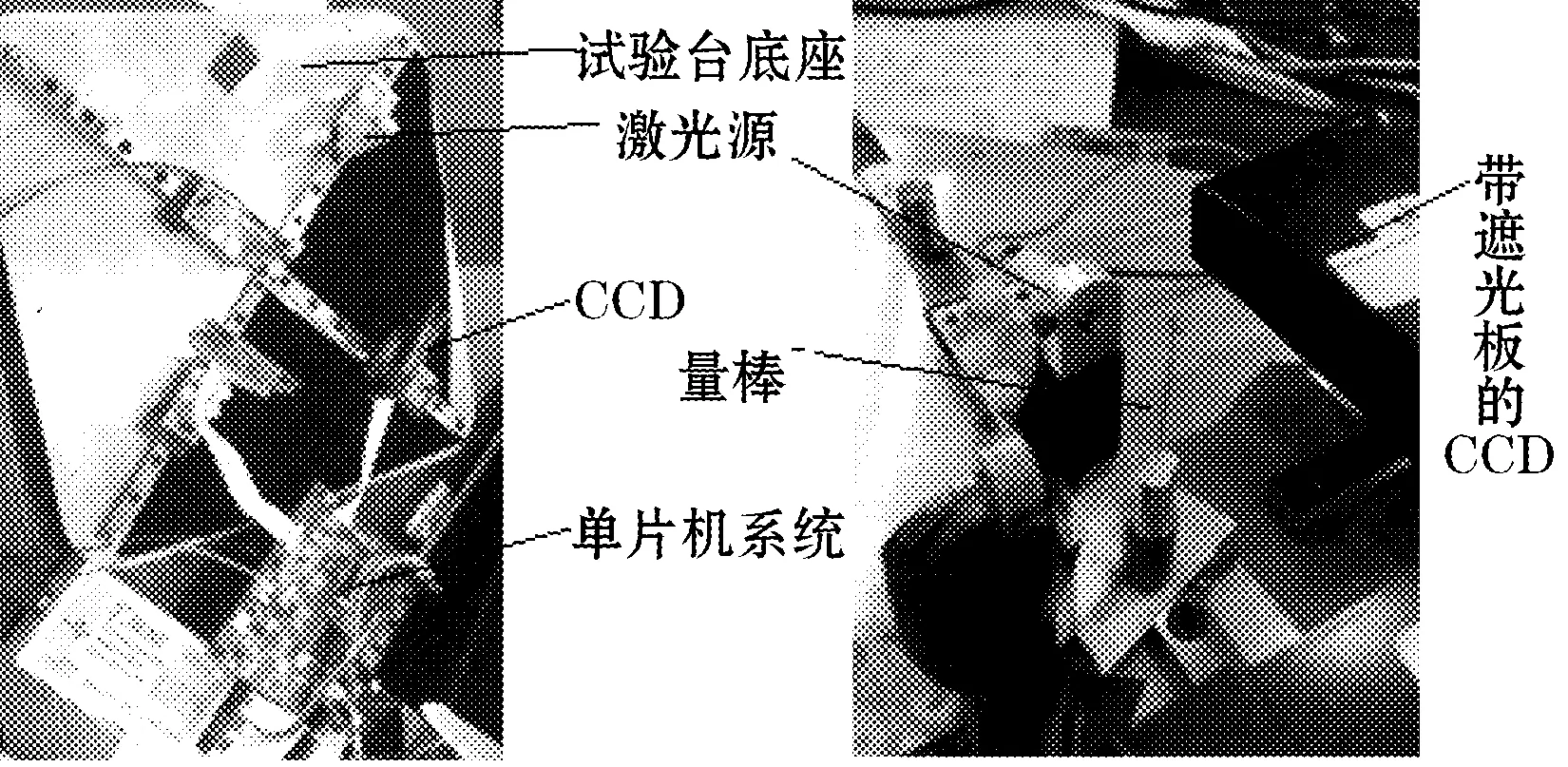
图7 实验台系统
3.2线径测量实验步骤
(1)定义CCD信号中左右阴影位置与另一路测得线径误差的二维关系,并在通过RS-232口将数据读到上位PC机,取定量棒直径为450 μm,CCD测得阴影波形如图8所示。
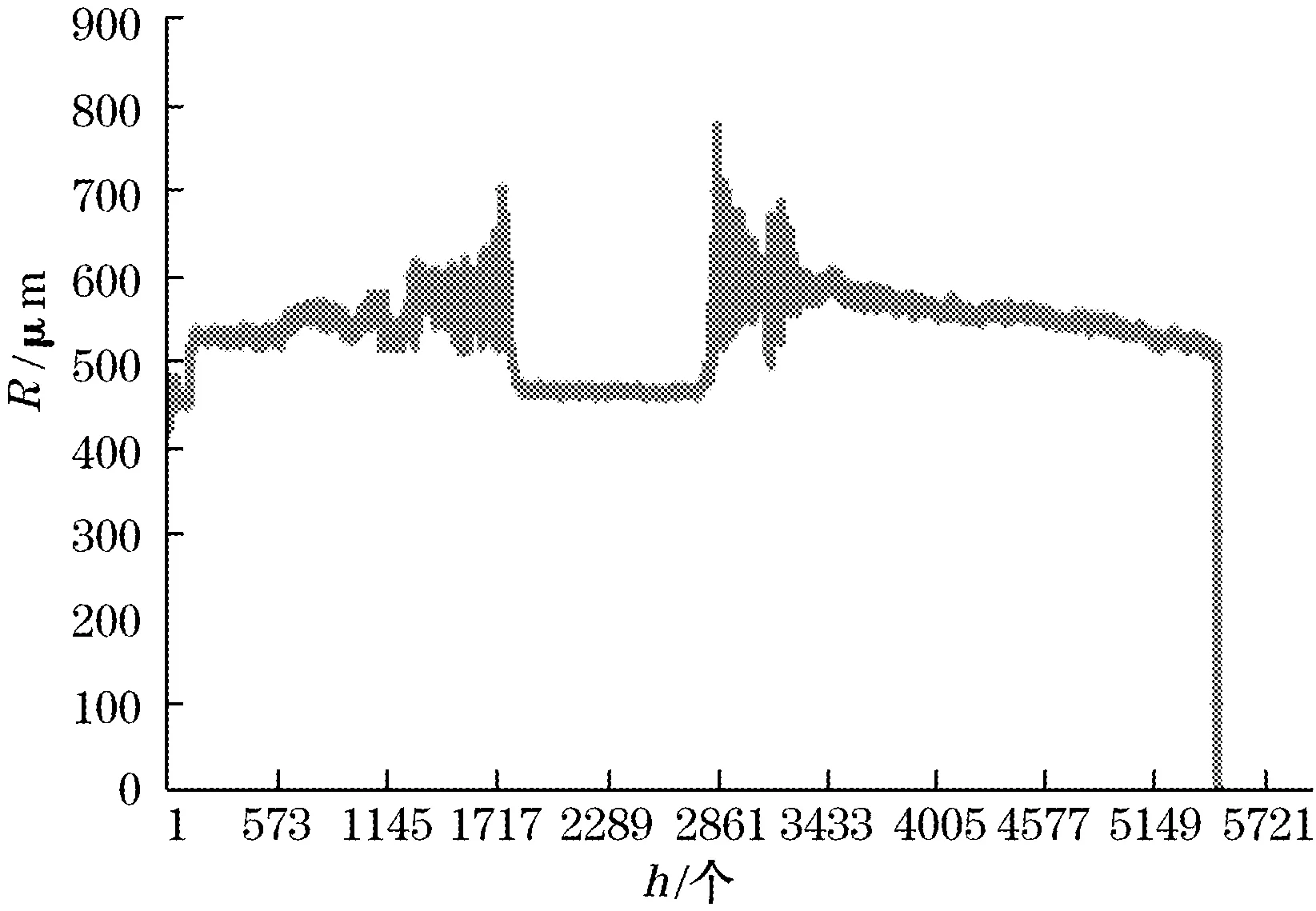
图8 CCD采集阴影波形
(2)Matlab中仿真左右阴影位置Rx,Ry,Lx,Lr与另一路测得线径误差的关系;
(3)线径拟合出阴影位置Rx,Ry,Lx,Ly被测线芯直径d之间的关系;
(4)拟合的参量回代到单片机系统中进行补偿修正;
3.3线径测量仿真结果分析
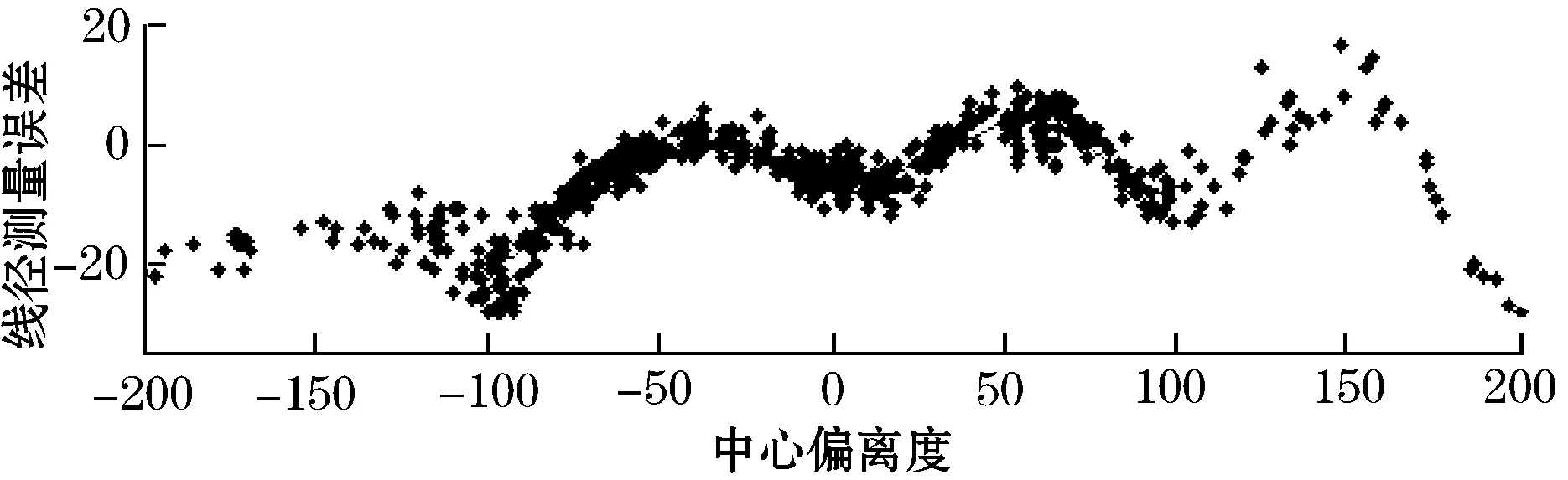
在keil中实现上述几何算法,并且分析系统误差源,在分析测得的两路CCD信号中的左右阴影位置对另一路测得的线径误差的影响,然后在Matlab中显示出相应的样本点,该实验取定中心偏离度-200~200 μm,通过观察样本点的误差,发现其样本点的波形类似于周期性的三角波,则可以分段对该波形进行一阶最小二乘拟合。在Matlab中观察拟合后的曲线,发现其拟合效果较好,基本能将误差控制在±2个像素点,拟合后效果如下。图9为X方向样本点及一次拟合曲线。

(a)450 μm X方向R路误差拟合中心偏离度
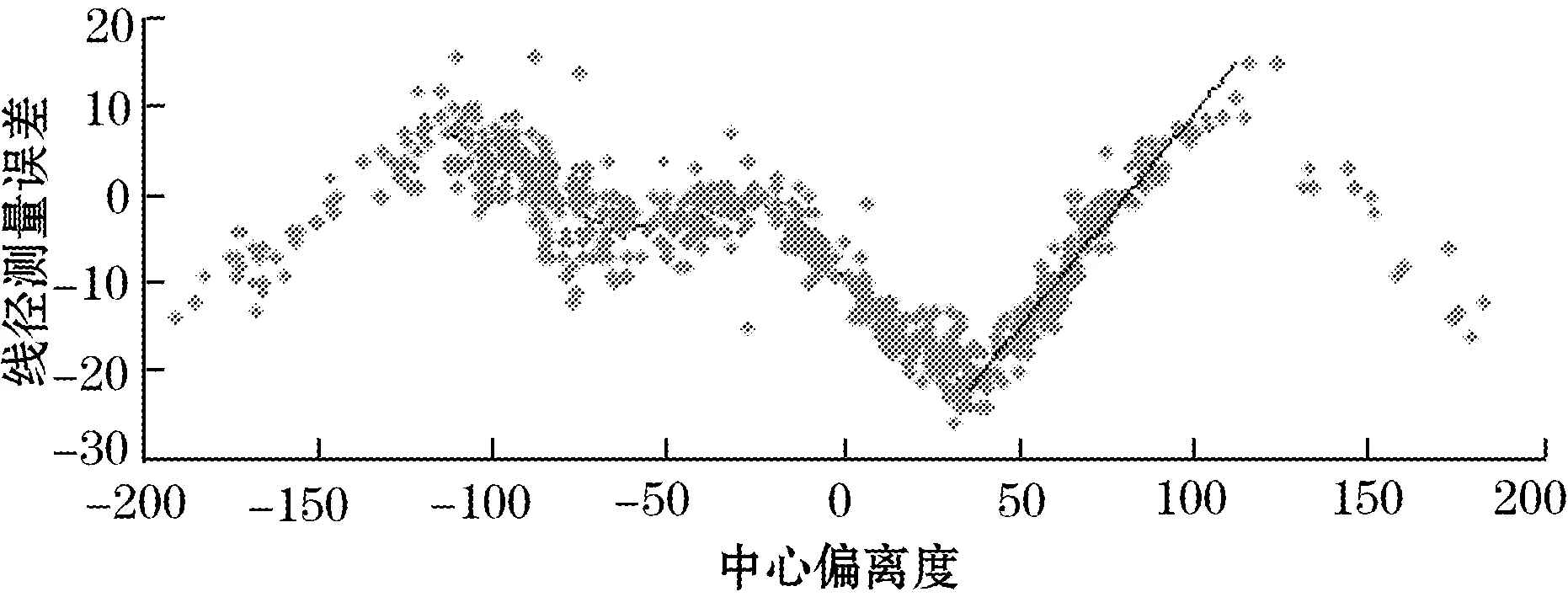
(b)450 μM X方向L路误差拟合中心偏离度
得到拟合参量见表1,然后将这些参数在keil中进行相应拟合补偿实验。
拟合后的误差效果基本能控制在-2 μm以内,因此,拟合补偿明显对误差的纠正有较好的效果。
(b)450 μmX方向L路误差拟合中心偏离度
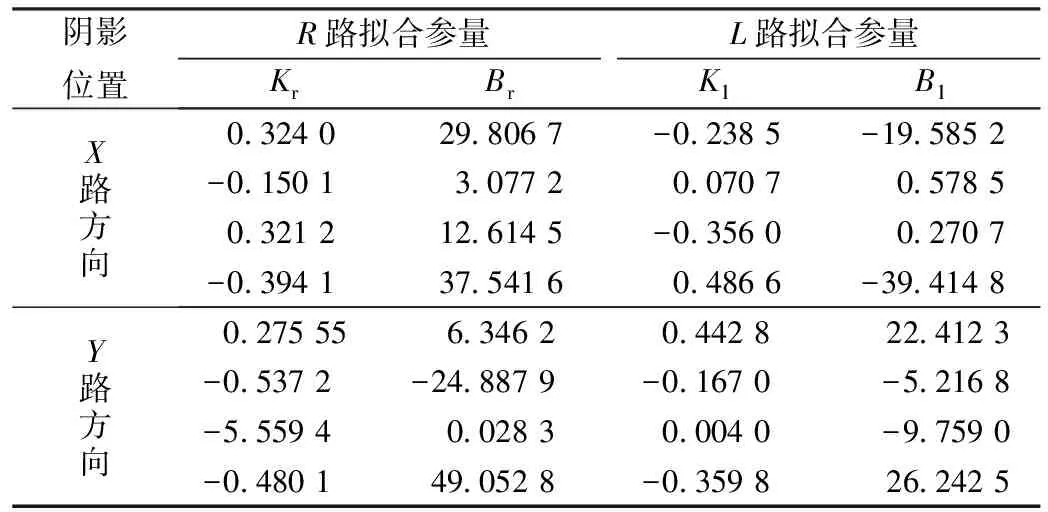
表1 最小二乘拟合参量
4 结束语
(1)文中利用最小二乘对阴影部分进行算法拟合补偿,修正了因为衍射造成的CCD检测到的阴影位置误差,使得在几何模型中的原始样本值更精确。
(2)在基于最小二乘数据拟合的边缘检测算法的基础上,针对所采集图像的过程,提出了一种优化光学几何模型的算法,和普通光学模型算法相比,改进的算法着重分析了优化的光学模型,在分析模型时不做近似处理,因此算法误差更小,这也进一步增加了测量精度。
(3)在系统中只对450 μm量棒进行了实验仿真,对于系列不同线径量棒还有待进一步的分析,找出规律,进行不同线径量棒的补偿,在后续研究中有待做进一步探讨分析。
参考文献:
[1]吴建兵 李川奇.CCD高精度线径测量.工业仪表与自动化装置,1996(1):27-29.
[2]雷波,卢红.基于线阵CCD的在线亚像素边缘测量系统,武汉理工大学学报,2010 (8):526-529.
[3]魏红伟,尤文,王宏志.高精度激光CCD在TP线径检测仪中的应用.吉林工学院学报,1994(4):68-72.
[4]李庆先.电荷藕合器件-CCD应用概述.仪表技术与传感器,1991(6):12-14.
[5]苏波,王纪荣.CCD高精度测径系统的研究.太原理工大学学报,2002,(5):506-509.
[6]ST hac.STM32F103 data sheet,2009.
[7]TOSHIBA hac.TCD1209D Image Sensors.TCD1209D datasheet,2001.
