基于BPNN的固相质量流量软测量方法

赵延军，程守光，高承彬，马翠红

(河北联合大学电气工程学院，河北唐山　063009)

0　引言

随着工业技术和科技水平的快速发展，气力输送粉料系统在化工、冶金、动力、轻工和军工等部门得到了广泛的应用，含有粉体粒子的气固两相流动在国民经济中占有重要地位。

多相流测固相质量流量虽然也存在许多非接触式测量法，如差压法、力学法、声学法、光学法、热学法等，但由于多相流流动的随机性和复杂性，严重限制了它们在工业上的应用[1]。因此多相流质量流量的在线测量已成为工业上亟待解决的关键课题之一。

弯管法流量计具有无附加压力损失、安装方便、适应性强、测量精度高等优点，但固相流量与其影响因素诸如压差、流量系数、气固混合密度存在着复杂的非线性关系，直接影响测量精度。近年来，人工神经网络迅速发展，具有适合于复杂、非线性、多变量、动态或难于建模的系统的特点，为解决各种实际工程问题提供了一种行之有效的方法[2]。

文中介绍了一种基于BP神经网络的双弯管法测量气固两相流固相质量流量的方法，在气力输送粉料系统中进行实验，获取了大量数据，并对4层BP神经网络进行训练，将固相质量流量测量中难于确定的影响因素反映到网络的连接权值中，实现了气力输送系统中固相质量流量的在线估算，为工业应用提供了一种切实可行的方法。

1　双弯管法测量原理

双弯管法测量气固两相流的固相质量流量的原理是：2个弯管(假定在保证2个弯管的弯径比相同，保证2个弯管在管道中气体的流动特性近似相同的情况下，其流量系数α相同)串联，在气固混合点之前安装一个弯管流量计来测量气体的流量，在混合点之后再安装一个弯管来测量气固两相流流经弯管时产生的差压，通过计算可得混合物中的固相质量流量[3]。

根据强制旋流理论[4]的计算公式，气固两相流流过弯管的两相混合物的质量流量qm为：

(1)

式中：qms为两相流中固相质量流量；qmg为两相流中气相质量流量；A为管道的流通截面积；ρ为两相混合物的密度；α为流量系数；R为弯管的曲率半径；D为弯管的半径；Δp2为气固混合点后的弯管内外壁的压差。

气体的流量为：

(2)

式中：ρg为气体的密度；Δp1为气固混合点前的弯管的内外壁的差压。

假设固相不占空间，因此

(3)

由式(1)、式(2)、式(3)整理可得

(4)

对于特定的输送管道，在输送气体的温度和压力一定时，气体的密度就是确定的，从式(4)可以看出固相质量流量与Δp1气固混合点前的弯管的内外壁的差压和Δp2气固混合点后的弯管内外壁的压差呈非线性关系。

由于两相流体流动的复杂性，理论模型计算出的流量与实际流量之间必然存在一定的误差，为了减小测量误差，引入了一个修正系数β即系统的综合流量系数，即：

qmr=βqms

(5)

式中：qmr为实际固相质量流量；β为系统的综合流量系数。

综合流量系数β主要与实验中的固气质量混合比、速度比、气相流体的特性、固相流体的特性等有关[5]。

弯管采用90°标准弯管，弯径比为1.5，内孔直径80 mm，曲率半径120 mm，取压孔位于45°方向上，弯管流量计采用精度等级0．2%的电容式(1151)4E型差压变送器，量程为0～6 000 Pa.弯管流量计的结构图如图1所示。

图1　弯管流量计结构图

2　基于BP网络的软测量模型及仿真

2．1神经网络的软测量模型

软测量技术是利用一组容易在线测量且与主变量密切相关的辅助过程参量，通过离线分析构造某种数学模型实现对主变量进行估算的方法[6-7]。测量模型是软测量技术的关键。通过对弯管流量计的理论分析，可以确定固相质量流量qmr与Δp1气固混合点前的弯管的内外壁的差压和Δp2气固混合点后的弯管内外壁的压差存在某种复杂的非线性关系。基于BP神经网络的软测量模型，可以避免弯管流量计的复杂计算和两相流动过程中的机理分析，实现对测量结果的良好逼近。文中以Δp1和Δp2作为4层BP网络的输入，建立了一种固相质量流量软测量方法，实现了对固相质量流量qms的在线估算。网络结构示意图如图3所示。

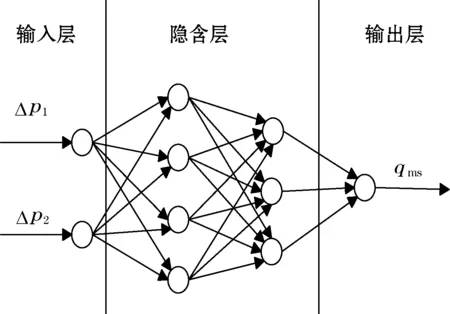
图2　网络结构示意图

BP网络中输出层的激励函数通常采用纯线性(pureline)函数，隐含层的激励函数采用S(Sigmoid)型函数：

(7)

为了提高训练速度和灵敏性以及有效避开Sigmoid函数的饱和区，一般要求输入数据的值在0和1之间，因此要对输入数据进行归一化处理[8]，归一化处理方法如下：

(8)

式中：xi为采集的原始数据中第i个元素；xmin为原始数据中的最小值；xmax为原始数据中的最大值。

BP神经网络的学习训练过程可分为4步[9]：

第一步前向计算。计算中间层各单元的输出bj和输出层各单元的响应Ct

(9)

bj=f(sj)

(10)

(11)

Ct=f(Lt)

(12)

(13)

(14)

第三步修正连接权值、利用各层个单元的误差对连接权值进行修正。

(15)

(16)

(17)

(18)

式中：pk为网络输入向量，pk=(a1，a2，…，an)；Tk为网络目标向量，Tk=(y1，y2，…，yq)；Sk为中间层单元输入向量，Sk=(s1，s2，…，sp)；Bk为中间层单元输出向量，Bk=(b1，b2，…，bp)；Lk为输出层单元输入向量，Lk=(l1，l2，…，lq)；Ck为输出层输出向量，Ck=(c1，c2，…，c3)；wij为输入层至中间层的连接权值；vjt为中间层至输出层的连接权值；θj为中间层个单元的输出阀值；rj为输出层的输出阀值；i=1，2，…，n；j=1，2，…，p。

第四步判断是否结束学习。选取下一个学习样本，执行上述计算，直到所有的样本训练完毕。当网络的全局误差小于预先设定的一个极小值时，即网络收敛。如果学习次数达到了预先设定的学习次数，则网络无法收敛，学习结束。

2．2模型训练与仿真结果

利用气力输送粉料系统的实验装置进行实验，共获取了25组实验数据，随机选取其中20组作为网络的训练样本，并将训练样本和其余5组数据作为网络的测试样本，来测试该BP网络的泛化能力。利用上述算法，对4层BP神经网络随机初始化后，进行了学习训练，经过10 696次训练之后，其平均误差达到了2.1%后，停止学习。

图3为BP神经网络训练结果，经过10 000多次的训练后，平均误差已基本上趋于平稳，并在规定的训练次数内达到了预期的期望。

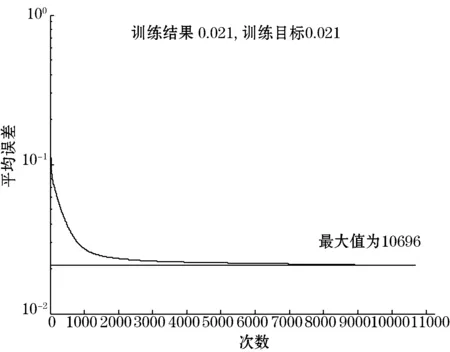
图3　BP神经网络训练结果

图4是软测量模型的仿真估算结果与实验数据的对比(其中*代表实验数据，○代表仿真结果)，从图中可以看出仿真估算结果在实验数据小范围内上下浮动，一致性较好，反映了该软测量模型良好的泛化能力。

图4　实验结果与仿真估算对比

图5是仿真结果的相对误差，从图5可以看出，BP神经网络经训练学习后，仿真估算结果的相对误差都在10%以内，反映了该BP神经网络软测量模型较好的测试能力。

3　误差分析

从图5中可以看出，虽然仿真估算结果的相对误差都在10%以内，提高了气固两相流固相质量流量检测精度，但是误差分布相对分散，这主要是由于气固两相流流体性质、流动状态以及流动条件的复杂性和多样性造成的弯管流量计对差压测量精度不高，如气固两相流流速不稳定、混合不均匀等因素。通过改善实验装置、提高弯管流量计测量精度，同时优化测量模型、网络结构和学习算法，能够有效提高煤粉质量流量的测量精度，更好地应用于工业生产中。

图5　仿真结果相对误差

4　结束语

在双弯管法测量气固两相流固相质量流量原理的基础上，建立了一种基于4层BP神经网络的软测量模型，经大量实验数据的学习训练后，全局误差低于0.5%，然后进行了预测仿真，仿真结果表明：估算值和实验结果一致性较好，大部分误差在5%以内，最大误差在10%以内，充分显示了神经网络软测量模型的良好逼近性能，为气固两相流固相质量的在线测量提供了一种有效方法。

参考文献：

[1]滕汜颖，李永光，周伟国，等．气固两相流动测量技术的现状与展望．上海电力学院学报，2002，18(4)：39-43．

[2]朱大奇，史慧．人工神经网络原理及应用．北京：科学出版社，2006．

[3]赵延军，李国光，王式民．双弯管法测量气固两相流质量流量的研究．计量学报，2005，26(2)：146-148．

[4]Armitage A．Neural networks in measurement and control．Measurement+Control，1995，28(7)：208-215．

[5]董群，王丽，任东海，等．固体质量流量测量技术进展．化工进展，2010，29(2)：1-4．

[6]俞金寿．软测量技术及其应用．自动化仪表，2008，29(1)：1-7．

[7]李勇，邵诚．软测量技术及其应用与发展．工业仪表与自动化装置，2005(5)：6-8．

[8]周开利，康耀红．神经网络模型及其MATLAB仿真程序设计．北京：清华大学出版社，2005．

[9]刘浩，白振兴．BP 网络的 Matlab 实现及应用研究．现代电子技术，2006(2)：49-51．