改进的直流静止测试法辨识永磁同步电机电感

林　杉，杨永立

(武汉科技大学信息科学与工程学院，湖北武汉　430081)

0　引言

永磁同步电机参数直接影响了控制器的性能[1]，因此准确辨识PMSM定子参数在控制领域有着至关重要的影响。近年来提出了几种永磁同步电机参数辨识的方法[2-4]。在线辨识通常采用高级算法，会带来复杂的计算。为了简化计算，离线辨识[2，3，5]方法运用起来更加简单，不存在算法收敛的问题，当电机处于静止状态下，电机模型可以得到简化。可以在设计控制器之前提供满足精度要求的相关参数。

直流静止测试法是一个有效的辨识电机电感的方法，该方法能减少控制系统和算法的复杂度，并且能实现电机转子自动定位。然而直流静止测试法通常是通过测量瞬态电压和电流值来辨识电感，测量的电感为某时刻的瞬态电感，其辨识精度易受到其它因素影响。

文中针对传统的直流静止测试法缺点进行分析，利用原有的直流静止测试法辨识实验系统，在电机进入静止稳态时辨识定子在某段时间内的平均电感，避免了由瞬态值的不精确性带来的辨识误差，解决了传统直流静止测试法存在的主要问题。

1　改进的直流静止测试法

1．1辨识方法基本原理

该方法在直流静止测试法辨识系统上改变PMSM端施加电压，将直流电压改变为直流电压和和小正弦交流电压的叠加电压，通过SPWM原理，利用IGBT逆变器产生实验所需电压。使电机A相与高电压端相连，B、C相并联在低电压端。此时电机等效电路图如图1所示。

图1　电机端电压施加原理图

设调制波为us=U0+Us·sinωst，载波为等腰三角波，三角波频率约为载波频率的9倍左右，设置调制波直流分量大于正弦分量幅值，使得PMSM端电压直流分量大于正弦电压幅值。当直流分量和正弦分量幅值比例满足一定要求时，转子在直流电压的作用下最终转到d轴并进入稳定静止状态，此时给定电压完全施加在d轴上。当电机处于静止时，电压方程为

(1)

由PWM调制产生的电压u(t)可由下列方程表示：

(2)

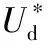
当电压施加到d轴时，d轴电流

(3)

分离出电机达到稳态后在正弦电压作用下的电压方程如式(3)：

(4)

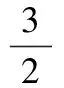
选取一段合适时间内，将电压和电流的时间方程带入式(3)积分计算得到d轴电感。

当辨识完d轴电感后，电机转子在0°位置，此时转子与A相对齐。关断IGBT，并对电机端重新施加一个相位超前d轴90°的电压，此时电压完全施加在q轴上，为了防止转子在电磁转矩下发生转动，使用煞车或副电网钳或力矩电机控制电机处于静止状态。同理分离出正弦电压响应下的电压方程，辨识q轴电感。

1．2调制电压产生原理

设三角载波uc的角频率为ωc，正弦调制波us的角频率为ωs．为了方便分析，把三角载波用两个分段函数表示。这样，三角载波的时间函数可写成式(5)形式：

(4)

正弦调制波的时间函数为：us=U0+Us·sin(ωst-φ)

设x=ωct，y=ωst-φ，直流电源为Ed，加入死区时间t0则SPWM波的时间函数uL为式(6)：

(6)

则uL的双重傅里叶级数表达式为式(7)

Bmmsin(mx+ny)]

(7)

(8)

(9)

当n=1为基波项，其方程由式(10)表示

A01+jB01=jMEd

(10)

2　仿真实验验证

2．1d轴电感辨识仿真

根据原有的直流静止测试法辨识系统开关频率，设定三角载波的频率为10 kHz．根据SPWM原理设置调制正弦波的偏置为0．032，幅值为0．008 1。由式(9)和式(10)可得施加给电机端电压Vc方程为：Vc=9.92+2.5sin100πt．

记录d轴电流波形图如图2，q轴电流波形图如图3。由于在MATLAB里，电机模型的转子位置为-90°，此时电机A相与q轴对齐，因此开始电压施加在q轴上，q轴电流产生电磁转矩，电机转子开始向施加电压方向转动，直到转子完全转到施加电压方向。

图2　辨识d轴电感时d电流仿真波形图

图3　辨识d轴电感时q轴电流波形图

由记录波形图可得，当t1=0．207 6 s时，id=6．81 A；当t2=0．212 6时，id=7．03 A．

因此d轴稳态电流方程为：

id=6.81+0.22sin[100π(t-0.0076)]

分离出正弦电压信号的响应有：

代入式中，得：

2．2q轴电感辨识仿真

当q轴存在电流时，电机会产生电磁转矩，为了保证电机在仿真中处于静止状态，在MATLAB中，将PMSM的输入端由转矩输入改为转速输入，并将值设置为零。此时电机q轴电流仿真图如图4，d轴电流仿真波形图如图5所示。

图4　辨识q轴电感时q轴电流波形图

图5　辨识q轴电感时d轴电流波形图

由仿真图可见，电机始终位于q轴处于静止状态，q轴电流波形与辨识d轴电感时d轴电流波形类似。由于PWM基波谐波和微小的互感，d轴此时存在幅值为数量级为10-11的正弦纹波。根据q轴电流波形图，选取合适的时间段，将测量得到的电压电流参数值带入公式计算得到q轴电感为6．52 mH．

3　仿真实验结果分析

对直流静止测试法仿真，当电压施加到d轴时，d轴稳态电流id=6．81 A，当id=4．3 A时，t=0．506 6 s，得时间常数τs=0．006 6，得Ld=6．41 mH．由于在MATLAB里面电机转子位于-90°位置，因此电压一开始就施加在q轴上，由于q轴存在电流产生电磁转矩，电机在0．004 s后开始转动，此时电压不在完全施加在q轴上。如抱死电机转子保证电机处于静止，电机最终不能进入稳态，无法通过测量电机瞬态响应时间常数辨识q轴电感。此时必须在转子转动前，通过测量q轴在某时刻的电流值，带入公式计算q轴电感辨识，由于实验器材精度限制，无法精确测量极短时间内的某时刻电流值，导致辨识精确度很低，很难准确辨识q轴电感。

表1　实验结果　mH

注：—表示实验条件下无法测量

4　结论

文中提出一种改进的直流静止测试法的新方法。介绍文中所提出方法的原理，其中包括辨识基本原理和实验给定电压产生原理。将文中提出的方法和直流静止测试法在MATLAB平台上进行了仿真实验，并对比两种方法的辨识结果，实验结果显示该方法相对于直流静止测试法在辨识度上有所提高，并且没有改变直流静止测试法的实验系统，由此可见改进的方法有效可行。

参考文献：

[1]HEIKO P,INGO H.Determination of Differential Inductances of Permanent Magnet Synchronous Machines for Sensorless Control.Proc IEMDC,2011：1579-1584．

[2]DAVID C，SORIN D．Parameter Determination Of Synchrnous Machine With Radial Permanent Magnets Using Analytical Calculation And Standstill Tests.Proc CCECE，2012：1-6．

[3]SHU Y，KANO T，YAMAGUCHI Y，et al．A Method to Determine Direct-and Quadrature-Axis Inductances of Permanent Magnet Synchronous Motors．Electrical Engineering in Japan，2010(171) ：41-45．

[4]程树康，于艳君，柴凤，等．内置式永磁同步电机电感参数的研究.中国电机工程学报2009(29) ：94-99．

[5]ERTAN H，B，SAHIN．Evaluation of Inductance Measurement Methods for PM Machines.Proc ICEM，2012：1672-1678．

[6]MARYAM K，NARAYAN KAR N C．Methods for Determining the Parameters and Characteristics of PMSM.Proc IEMDC，2011：955-960．

[7]RUKMI D，RAHMAN M F．A Comparative Analysis of Two Test Methods of Measuring d- and q-Axes Inductances of Interior Permanent-Magnet Machine．IEEE transactions on magnetics，2006(42)：3712-3718．

[8]汤斯．永磁同步电机参数辨识研究[学位论文]．武汉：华中科技大学，2009．

[9]SHU Y，GOTOU T，ARA T．Prediction of the Operational Impedance of Rotating Machines by Various DC Testing Methods．Electrical Engineering in Japan，2004(147)：51-59．

[10]TAO S，KWON S，JEONG-JONG L，et al．An Improved AC Standstill Method for Testing Inductances of Interior PM Synchronous Motor Considering Cross-magnetizing Effect.ProcECCE，2009：2415-2422．

[11]SEBASTIAN E，BERNHARD P．Identification of Differential Inductances of Permanent Magnet Synchronous Machines Using Test Current Signal Injection.Proc SPEEDAM，2012：1342-1347．

[12]刘凤君．现代逆变技术及应用．北京：电子工业出版社，2006．

[13]D．HOLMES G，LIPO THOMAS A．电力电子变换器PWM技术原理与实践．北京：人民邮电出版社，2010．