数据驱动的大规模水面动画合成方法

王承博，朱登明

(1.中国科学院计算技术研究所虚拟现实实验室，北京 100190；2.中国科学院大学，北京 100049)

水是自然界中最为普遍的物质之一，它的存在使得世界更加生动多样。随着多年的研究发展，水的动画合成与模拟取得了大量的研究成果，并被广泛地应用于虚拟现实、影视动漫、游戏娱乐等行业中，极大提高了场景的真实性。传统的水动画合成方法可以分为两类：基于波面造型的方法和基于物理的方法。基于波面造型的方法通过参数曲面合成和噪声合成的方法近似模拟水表面的高度场，此类方法运算量小，可以达到实时，但是生成的水面简单，缺乏细节。基于物理的方法通过求解流体动力学方程来模拟水的运动，此类方法合成的水面具有高度的真实感，但其包含大量的数值计算，求解步骤复杂且非常耗时。

基于视频的方法是近几年才逐渐发展起来的一种研究思路，该方法直接从自然现象中提取特征进行表面重建，具有内在的物理真实性，并且抛开了复杂的物理方程求解，计算速度得到了提高。但目前已有的方法其结果受限于拍摄范围和重建精度的制约，不能在规模和细节之间取得较好的平衡。本文提出了一种新的合成框架，基于视频重建出具有各种运动细节的水面，然后对这些水面进行采样，将采样出的等大小的规则面片进行有重叠的融合拼接，从而得到细节丰富且具有任意规模的水动画。

1 相关工作

1.1 基于视频的水面重建

从视频中提取流体运动信息进行表面重建从而合成水面动画是一个较新的研究方向，近年来已有的研究方法根据重建对象的规模大小可以分为两类：室内可控水体重建和室外大规模水体重建。

针对室内可控水体的重建方法，大多需要对水面进行特殊处理来消除水的折射和镜面反射。Ihrke等[1]利用多台摄像机对水进行拍摄，在拍摄前先向水中添加了荧光化学物质，在黑暗的环境中拍摄，然后利用光的强度计算水体厚度，从中构造出水体的粗糙模型，最后对基于图像一致性的误差函数进行优化得到光滑的流体表面。Wang等[2]使用双目摄像机，拍摄前对水进行染色，并将一个固定的随机斑点图案投影到液体表面，在黑暗的环境中拍摄，从图像中提取出深度图并根据张力约束和速度场约束进行优化得到重建的表面。Sagawa等[3]向表面投影具有特殊结构的图像，根据图像的形变来恢复快速变化的表面，包括水面、服装和人脸等，其中在对水面重建时也对水面进行了染色，消除了折射的影响。以上三种方法都对水面进行了特殊处理，重建的细节较好，但步骤繁琐，计算量较大。Morris和Kutulakos[4]对运动的浅水表面进行复原，作者在水的底部放置了一个未知的图案，用两台摄像机进行拍摄，综合利用立体成像和折射成像的方法，虽然没有对水体进行特殊处理，但其局限于对浅水的微小波动进行重建。

另一类方法针对的室外大规模水体主要指江河湖海等流体，此类流体浑浊不透明，镜面反射和折射现象较弱，可近似为朗伯表面。Gallego等[5]使用两台摄像机拍摄海洋表面，提出一种基于双目视觉的方法对海面进行重建，结合物理方程，进行了大量数值计算，重建精度较高，但是计算复杂耗时。Pickup等[6]将基于影调恢复形状(shape from shading, SFS)[7]和光流的方法相结合，先用SFS获取初始的表面，然后利用基于初始的表面使用光流来追踪速度场，最后通过速度场来重建出水面，重建结果具有较好的视觉逼真度。

以上重建的方法只能针对镜头内的水体运动进行复原，得到的结果由于拍摄的限制显现出片面局部的缺点，并不能直接满足实际的应用需求。为此，本文应用拼接的思想，利用重建的局部结果合成整体。

1.2 拼接

拼接在纹理合成领域是一个重要的研究方向，纹理的拼接是指由已知的纹理图片拼接合成出更大规模的纹理图像，在游戏贴图中的应用较多。基于块的拼接方法首先由Efros和Freeman[8]提出，其大体算法是从已知的纹理图像中采样出小的纹理块，然后有重叠地放到目标纹理图像中，在重叠区域使用误差最小的准则进行切割。该方法计算简洁高效，但是采样的块必须等大小且规则放置，适用于周期重复的纹理。Kwatra等[9]对其进行了改进，建立马尔科夫随机场模型并用GraphCut进行分割，对于块的放置没有限制，切割线更加随机，能适用于更多的纹理图像。

以上是纹理的二维拼接方法，本文重建出来的三维曲面水面，在曲面细节和连续性上提出了更高的要求。三维曲面的拼接方法大致分为两类：基于泊松方程的方法[10]和基于拉普拉斯坐标的方法[11]。这两类方法具有一定的通用性，适用于多种曲面编辑的操作，但这些方法均只针对于静态的网格表面，且计算复杂，没有考虑水表面的特性，不能直接适于本文的场景。针对动态网格序列形式的扩展拼接还没有专门的研究。

本文将首先利用基于SFS推导的方法从视频中重建出水的深度表面，进行了一系列的优化得到三角网格面，然后通过针对三维表面序列设计的拼接方法，从重建的局部结果采样合成最终结果，下面分别详细介绍重建和拼接算法。

2 水面重建

本文的重建目标是针对室外的大规模水体，由于此类水体浑浊不透明，具有朗伯表面的性质，Pickup等[6]利用SFS方法得到了较好结果。

SFS方法假设图像的亮度与物体表面的辐射图成正比，对于朗伯表面，物体的表面辐射图又是光线方向与表面法线夹角的余弦值，可得下式：

其中I(x,y)为像素值，R为辐射图，为光源方向，n=(p,q,1)为表面法向。Tsai和Shah[7]的方法采用线性逼近，迭代求解的方程如下：

令迭代的初值为Z0(x,y)= 0，迭代一次的结果为：

可见经过一次迭代生成的结果与原图像成正比Z1～I。为此本文采用对图像进行归一化处理的方法，将得到的灰度图作为深度结果：

这样重建出的表面与真实的表面之间存在着一些明显的差异，这些差异是由SFS问题的不适定性导致的，文献[7]的方法进行多次迭代也不能修正。但由于重建的表面序列具有较好的波动特性和较真实的视觉体会，对于本文动画合成的需求来说已经足够。

以上重建是基于每一帧独立处理的，各帧之间可能会由于光线的变化使得结果不规整，需要做一些处理来满足各帧之间的连续性。本文利用体积守恒做约束，对重建的表面做对齐优化。记水体的高度表面为h′(x,y,t) =h(x,y,t) +δ(t)，h(x,y,t)是基于视频重建的表面，δ(t)是每帧的平均误差。体积是表面的积分，体积守恒的约束可以表示如下：

离散形式为：

简单地令C=0，得到了修正的水表面模型：

为保证重建表面的时空连续性，本文对以上结果再做一些平滑处理。先对每帧进行拉普拉斯平滑，由于直接重建出的是深度表面，将权重取为1，这样在拉普拉斯平滑时不会改变表面在水平方向的规则分布。接下来用各帧做差求出垂直方向的速度场 并用高斯滤波进行平滑处理，之后再从平滑过的速度场中计算出各帧表面。最后根据以上优化的结果构造出三角网格，图1是整个处理流程。图2是两个不同水面图像的重建结果。

图1 水面建模流程

3 三角网格拼接

3.1 拼接准则

重建出水面序列以后，类似纹理合成那样，本文利用有限的表面去合成更大规模的表面。由于这里拼接的是连续的表面序列，问题的空间是ℝ3×T，T为时间域，因此不仅要保证每一帧拼接后在三维空间的连续性，更要保证相邻帧之间的连续性，即在时域的连续性。记表面序列的集合为St，本节中提到的表面均指的是St，而不是具体的一个表面。

本文采用基于块的合成方法，首先将表面St正交投影到水平面上得到St，计算出St所在的包围盒并将其划分为n×m的矩形网格，如图3所示。将落在同一个网格内的顶点和对应的垂直速度求平均值存在网格中，作为一种粗糙的参数化结果。

图2 从左至右依次是原图像，重建出的三角网格和从重建表面渲染的结果；下面一排是基于红色方框区域的重建

图3 平面网格映射

然后以网格为最小单位进行采样，采样的块记作B(s,l)，s表示其在投影表面S上起始位置的网格坐标(is,js)，l=(r,c)表示其大小，r和c分别为其占有的网格的行数和列数。如图3中蓝色区域为起始于(2,2)，大小为(5,5)的块。

采样的块将被有重叠地放置到目标区域，按照从左到右、从上到下的顺序合成目标。为了使合成后的结果能同时满足空间和时间的连续性，假设两个相邻块的重叠区域为1T和T2，它们第一帧的表面分别为1φ和2φ，速度场分别为Vt和Wt，定义1T和T2的距离为：

当我们采样出所有的块并放到目标区域后，下一步对重叠的区域进行合并处理，处理的过程总共分为三步：裁剪、融合与缝合。下面将一一详细介绍。

3.2 裁剪

裁剪是将重叠区域从原来的表面裁剪下来成为独立的网格面。将部分表面裁剪下来是为了便于做局部参数化，以提高整体的计算速度。通过上节中的水平网格来界定裁剪区域，如图4所示蓝色网格为裁剪框，有两种裁剪方法：细裁剪和粗裁剪；细裁剪将严格依照轮廓线进行裁剪，在裁剪边界处重构三角网格结构，使其具有规则的边界。而粗裁剪则仅提取裁剪框内的三角网格，不修改已有结构，速度较快，但会产生不规则边界。实验在后面进行的参数化操作削减了边界不规则性的影响，因此通常采用效率更高、更稳定的粗裁剪。

图4 细裁剪与粗裁剪

3.3 融合

通过裁剪可得到两个网格面S1,S2。将S1和S2融合为一个网格面S3，S3能自然地从S1过渡到S2，如图5所示。需首先建立S1和S2之间的一一映射。把S1和S2都参数化到单位正方形区域，两个网格面上最靠近包围盒四个角的四个顶点被分别映射到单位正方形的四个顶点，网格内部的点通过中值坐标参数化。

图5 黑色网格为红色和绿色网格重叠部分的融合结果

记 ℝ3中的点为p= (x,y,z)，中的点为u=(u,v)，中的三角形用大写字母表示，中的三角形用小写字母表示，如T=[p1,p2,p3]和t= [u1,u2,u3]。参数化的结果用花体英文字母表示，如S是S的参数化结果。通过两个网格面的参数化平面的坐标来建立一一映射。由于两个网格边的结构不一样，很难将一个面上的顶点映射到另一个面的顶点，大部分情况下只能将一个网格面上的顶点映射到另一个网格面的三角形中。假设u1∈S1被映射到三角形t∈S2，可计算出u1对应点的重心坐标。定义三角形 的三个顶点为t1，t2和t3，u1对应的点可以表示为这三个顶点的加权和：

其中 (λ1,λ2,λ3)就是重心坐标，满足约束λ1+λ2+λ3=1。重心坐标的计算方式如下式：

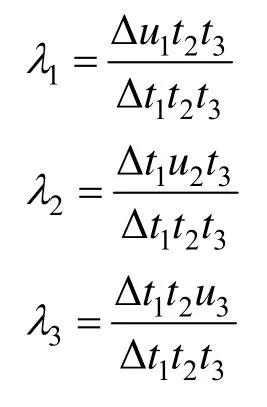
式中Δ表示面积，如图6所示。

图6 重心坐标计算

接下来利用在参数化平面找到的对应关系，将原始表面的对应顶点进行线性插值。本文直接令融合表面S3的结构等同于S1，S3的顶点位置计算如下式：

式中，p1∈S1，p2=λ1q1+λ2q2+λ3q3，且w∈ [0,1]。如果希望融合表面沿参数化平面的u轴过渡则令w=u1，沿v轴过渡则令w=v1。

3.4 缝合

最后一步需要把S3与原来的表面缝合在一起。前述处理过程得到的S3与原来表面的边界紧密相邻，缝合操作需要将相邻的边界线合成一条。

首先利用弧长把相邻的边界线参数化到[0,1]的线段。记相邻的边界为B1=和B2=，参数化结果为：

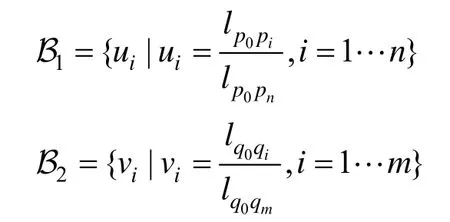
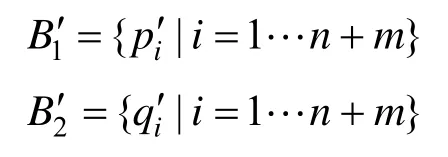
和的顶点之间一一对应，在此基础上构造新的公共边界B′ =，使得它到和的距离平方之和最小：

当si-=si-时上式取得最小值，因此定义新的边界为：

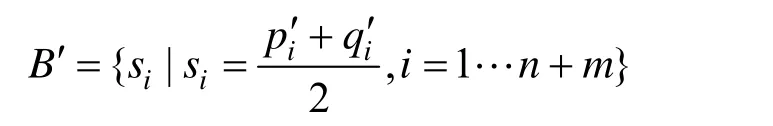
用B′替换1B′和 2B′，并根据B′修改原网格面的三角结构得到融合的表面，如图7所示。

图7 缝合

4 实验结果与讨论

本文重建的视频来源于Dyntex数据库[12]和自己用手机拍摄的湖面。实验运行在有Core-i3M380 2.53 GHz的CPU和2 GB内存的计算机上。

根据水面的运动特性，人工地把视频数据进行分类并筛选出四种代表性的水面，分别是：粗条纹波面，细条纹波面，短鳞波面和杂波面。本文对这四种水面重建并进行4倍拼接扩展。在进行网格划分时，网格越细扩展的结果连续性越好，但是计算量就越复杂，经过多次实验发现每个网格包含四到八个顶点就能得到不错的结果。图8展示了四种波一帧的重建和拼接结果。从结果中可以看到，拼接的结果没有任何缝隙，不仅具有整体的水面运动特性，也拥有较好的细节。图9展示了粗条纹波扩展后的六帧结果，可以看到扩展的结果在时间上也有较好的连续性。视频结果参见http://v.youku.com/v_show/id_XNTYxMDQyNzQ0.html。

图8 从左到右依次是原图像，重建的表面，4倍拼接的表面和拼接结果的细节展示；从上到下依次是粗条纹波面，细条纹波面，短鳞波面和杂波面

图9 粗条纹波的扩展结果，截取了六个等间隔的帧

本文重建出的水面序列是基于真实水面运动的视频记录，其物理真实性依赖于数据和重建算法。在后续的合成阶段，利用的是表面的相似性进行扩展，此时局部的物理真实性可以得到保障，但整体的物理真实性无法保障，从有些视频结果中可以看出局部痕迹。由于本文的目的在于动画，降低了对整体物理真实性的要求，依赖距离最小原则，保障了整体的视觉真实性。

5 结束语

本文提出了一种新颖的水面动画合成方法，从单目摄像机拍摄的视频中提取出三维水面序列，继而用拼接的方法合成出任意大小的三维水面序列。该方法可以方便地应用到影视游戏中，根据用户需求定制任意规模的水面动画。本文提出的基于三角网格面的拼接方法可以通用地适用于任何方法得到的三角网格表示的水面模型。在将来的工作中需综合各种重建方法，收集更多类型的水面运动序列，建立丰富的水面运动数据库，并进一步加强本文的拼接算法，实现将各种类型的水面在时间和空间上的混合融合，提高合成结果的多样性。

[1]Ihrke I, Goidluecke B, Magnor M.Reconstructing the geometry of flowing water [C]//Computer Vision, 2005.ICCV 2005.Tenth IEEE International Conference on.IEEE, 2005, 2: 1055-1060.

[2]Wang Huamin, Liao Miao, Zhang Qing, Yang Ruigang,Turk G.Physically guided liquid surface modeling from videos [J].ACM Transactions on Graphics (TOG), 2009,28(3): 1-11.

[3]Sagawa R, Kawasaki H, Kiyota S, Furukawa R.Dense one-shot 3D reconstruction by detecting continuous regions with parallel line projection [C]//Computer Vision (ICCV), 2011 IEEE International Conference on.IEEE, 2011: 1911-1918.

[4]Morris N J W, Kutulakos K N.Dynamic refraction stereo [C]//Computer Vision, 2005.ICCV 2005.Tenth IEEE International Conference on.IEEE, 2005, 2:1573-1580.

[5]Gallego B G.Variational image processing algorithms for the stereoscopic space-time reconstruction of water waves [D].Georgia Institute of Technology, 2011.

[6]Pickup D, Li Chuan, Cosker D, Hall P, Willis P.Reconstructing mass-conserved water surfaces using shape from shading and optical flow [C]//Computer Vision-ACCV 2010.Springer Berlin Heidelberg, 2011:189-201.

[7]Tsai PS, Shah M.Shape from shading using linear approximation [J].Image and Vision Computing, 1994,12(8): 487-498.

[8]Efros A A, Freeman W T.Image quilting for texture synthesis and transfer [C]//Proceedings of the 28th annual conference on Computer graphics and interactive techniques.ACM, 2001: 341-346.

[9]Kwatra V, Schödl A, Essa I, Turk G, Bobick A.Graphcut textures: image and video synthesis using graph cuts [C]//ACM Transactions on Graphics (ToG).ACM,2003, 22(3): 277-286.

[10]Yu Yizhou, Zhou Kun, Xu Dong, Shi Xiaohan, Bao Hujun, Guo Baining, Shum H Y.Mesh editing with poisson-based gradient field manipulation [C]//ACM Transactions on Graphics (TOG).ACM, 2004, 23(3):644-651.

[11]Sorkine O, Cohen-Or D, Lipman Y, Alexa M, Rössl C,Seidel H P.Laplacian surface editing [C]//Proceedings of the 2004 Eurographics/ACM SIGGRAPH symposium on Geometry processing.ACM, 2004: 175-184.

[12]Péteri R, Fazekas S, Huiskes M J.DynTex: A comprehensive database of dynamic textures [J].Pattern Recognition Letters, 2010, 31(12): 1627-1632.