一种求含孔洞多边形交、并、差集的新方法
2014-03-21郝永兴
赵 军,郝永兴
(兰州交通大学机电工程学院,甘肃 兰州 730070)
多边形的交、并、差集运算是计算几何、计算机图形学的一个基本问题。对这一问题的研究在多个领域具有重要的理论与实践意义,诸如GIS系统中进行叠加分析、几何造型中隐藏线的消除、线路板中电子元件的布局和线性规划等。目前,针对这一问题国内外也进行了不少研究,提出过一些算法[1-10],其中有些不能处理含孔洞多边形。周培德[5]提出了一种较为可行的针对含孔洞多边形的算法,其算法复杂度为O(n2logn)。朱雅音等[6]通过扫描线法并利用多边形的拓扑信息确定任意多边形的交、并、差集,其算法复杂度为O((n+m+k)log(n+m+k)),其中m,n是多边形顶点数,k是两多边形的交点数。刘红军等[7]以两多边形差集为基础解决了布尔运算问题,可以解决多边形含孔洞问题,但算法中多边形求交后每段线段的中点需要进行点包含运算,使其算法复超过O(n2)。朱二喜[8]提出图形内角的概念,并利用它确定两个任意多边形的交并差,算法复杂度为O(k(n+m))+O(n+m+k)。崔璨和王结臣[9]基于梯形剖分求解多边形布尔运算,所提算法可以处理含孔洞多边形,时间复杂度为O(nlogm),m为位于同一扫描条带上小线段的平均数。本文在文献[10]的基础上进一步提出一种解决含孔洞多边形布尔运算的方法,通过构造的一条双向“桥边”,使内环顶点序列并入外环顶点序列中,以消除内环,将多环顶点序列转换为单环,以便利用不含孔洞多边形布尔运算的交并差算法。针对两个多边形环包含嵌套的奇异情况,通过多边形和点的包含性来确定嵌套关系。整个方法时间复杂度为O((n+m+k)logd),其中d为多边形分割的单调链数[11]。
1 相关概念
(1) 最小回路:其内部没有与其共边的其他回路。
(2) 顶点的关联边:如果边e以顶点v为其一个端点,则称边e是顶点v的一条关联边。
(3) 顶点关联边序列:平面上s条具有公共顶点m的边e1,e2, …,es,根据各边与过m点水平向右方向逆时针夹角的大小进行的一个排列,记为CElist_m。
(4) 顺时针最小转角:平面图中关联于同一个节点m的s(s>2)条边e1,e2,…es,将ei(1≤i≤s)以m点为中心绕平面法矢n顺时针旋转遇到第一条边ek(1≤k≤s),称ek对ei具有顺时针最小转角。
(5) 多边形内点在边界的可见点:对简单多边形P和多边形平面内的视点z,若P边界上的点v与视点z的连线在P内部,则称v点相对于视点z是可见的。
(6) 点包含性检测:判断一点z在简单多边形P的内部、外部或者边界上。
为了便于描述,设P、Q为两个输入多边形,用P∩Q、P∪Q、P-Q分别表示多边形P与Q的交集、并集和差集。
2 多边形的初始化
2.1 多边形的多环转换为单环
为了解决含空洞多边形的布尔运算,利用简单多边形内一点的边界可见点,通过增加一条双向“桥边”,将含孔洞多边形多环转换为单环,以此来解决含孔洞多边形由于多环的存在而较为困难的布尔运算问题。如图1(a)所示多边形P,具有两个环,外环P-out={1,2,3,4,5},内环P-in={6,7,8,9},通过构造双向“桥边”6v1,将P的内外环合并为一个环P={1,2,3,v1,6,7,8,9,6,v1,4,5}如图1(b)。

图1 含孔洞多边形的转换
具体转换步骤为:
将多边形外环初始化为逆时针方向,内环初始化为顺时针方向,使得多边形内部区域始终位于有向边界的左侧。选择内环中的最右顶点,作为外环的一个内部点在外环边界上搜寻可见点。搜索多边形可见点的方法参见文献[12]。将搜索到的可见点以及内环最右顶点作为二重顶点,并将其置于该内环顶点序列的首尾一并插入多边形的外环序列中,消除一个内环。如此进行直至所有内环均被消除。
比如多边形P:P-out={1,2,3,4,5};P-in={6,7,8,9}、{10,11,12,13},内外环方向如图2(a)所示。顶点6为内环顶点中最右顶点,找出其在外环边界上的一个可见点v1,如图2(b)。将顶点序列段{v1,6,7,8,9,6,v1}插入外环序列,则P-out={1,2,3,v1,6,7,8,9,6,v1,4,5},消除了一个内环。再找出剩余内环顶点中的最右顶点10,找出其在外环边界上的一个可见点v2,将顶点序列段{v2,10,11,12,13,10,v2}插入外环序列,则P-out={1,2,3,v1,6,7,v2,10,11,12,13,10,v2,8,9,6,v1,4,5},至此则消除了所有内环。
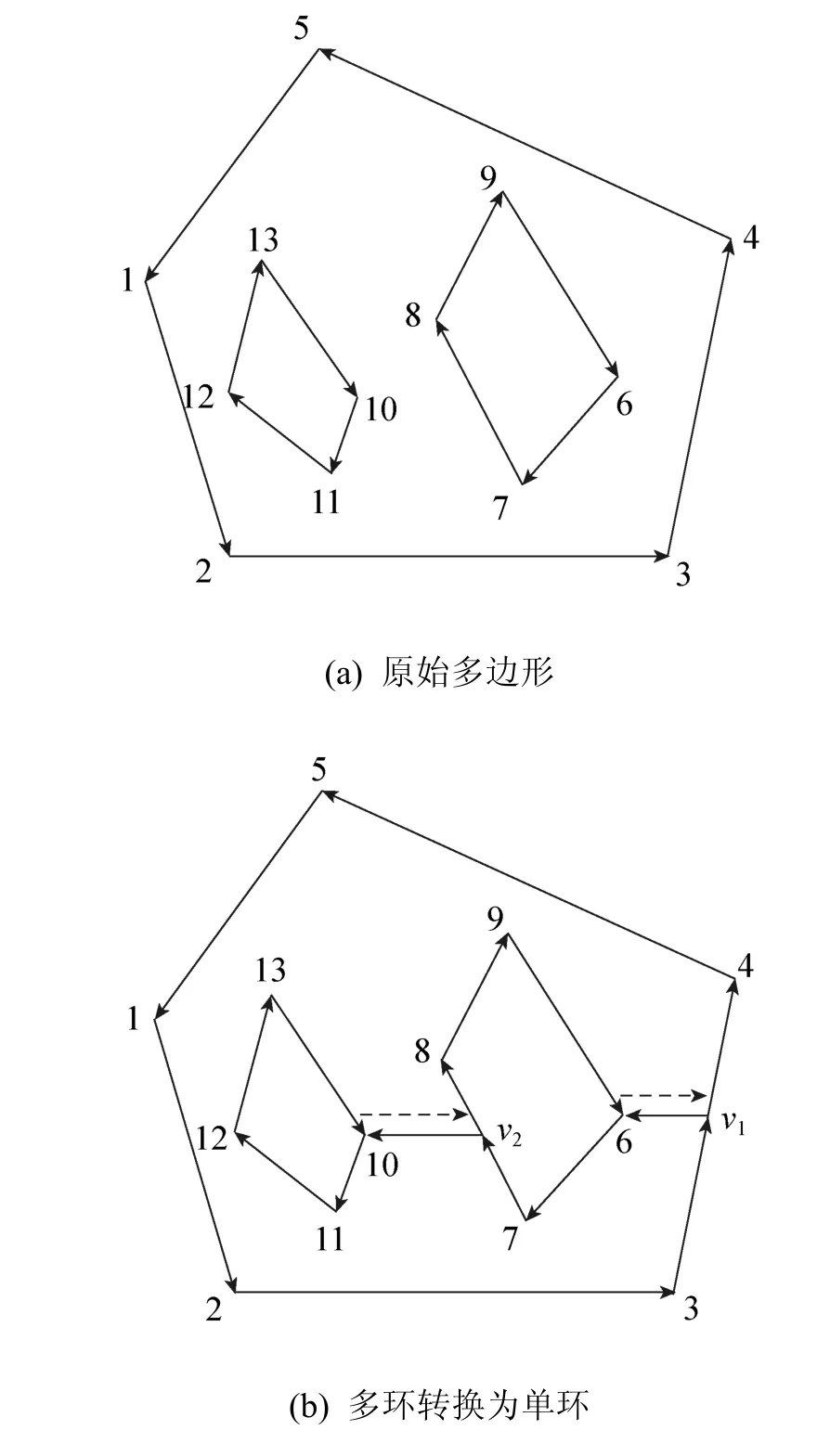
图2 含多孔洞多边形的转换
2.2 两个转换后的单环相交
两个转换为单环的多边形P={p1,p2,…,pn}与Q={q1,q2,…,qm},求出各边的交点,并对交点处各关联边进行排序。对P与Q各边交点的计算,可采用Park和Shin[11]提出的基于多边形单调链的方法。求出P与Q的所有交点后,分别在P与Q顶点序列中将非顶点交点插入到相应位置处。
在每个交点关联的四条边中,根据各边在多边形中的方向,有两条边指向交点,称为与交点关联的负向边,有两条边背离交点,称为与交点关联的正向边。“桥边”是特殊的双向边,如果多边形的边与另一个多边形的“桥边”相交,则在交点处的关联边中“桥边”是一条边但具有两个方向。也就是说与交点关联的“桥边”段既是正向边又是负向边。如图3中,多边形P和Q相交,P的边pipi+1与Q的“桥边”v1qs相交于m点,在m点的四条关联边中,mqs、mv1和mpi+1关于m为正向边,pim、mv1和qsm为关于m的负向边。m点处的关联边序列CElist_m={mv1,pim,mqs,mpi+1}。各个内环的最右顶点以及其外环边界的可见点均亦视为交点。
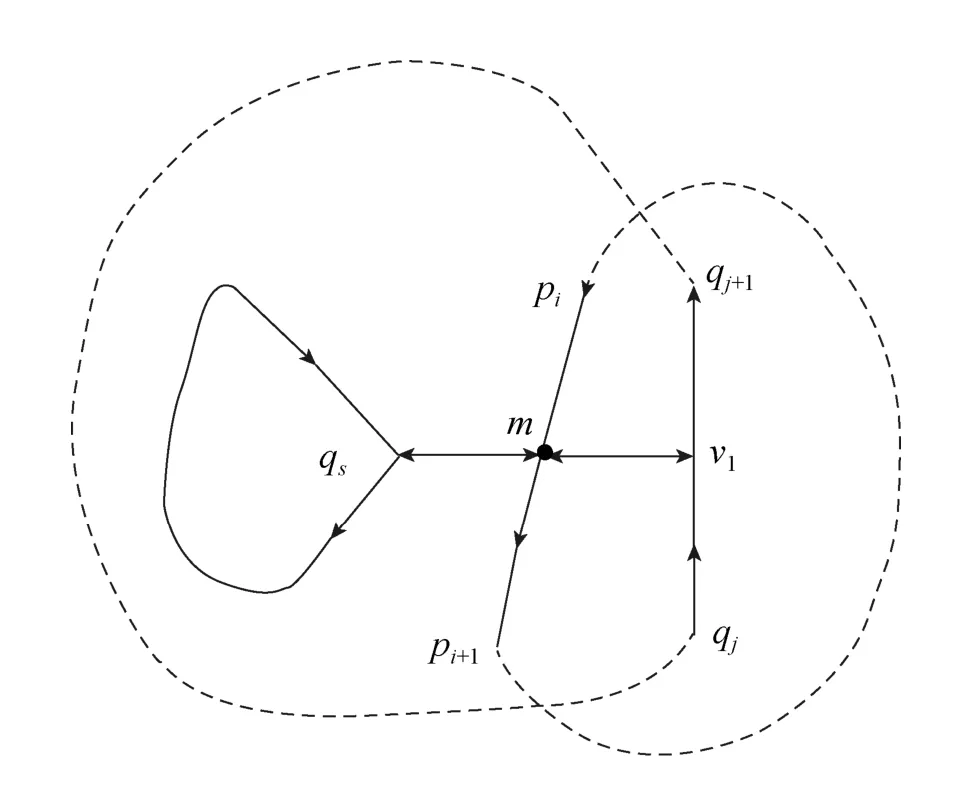
图3 与“桥边”相交的关联边情况
为了便于搜索最小回路,对关联于交点的四条边按照与水平向右方向成逆时针夹角的大小进行排序,即确定交点处的关联边序列。
3 两个多边形交、并、差
将两个含孔洞多边形由多环转换为单环,求出两个环的交点,将交点关联边排序后,沿交点关联正向边按照最小转角原则搜索最小回路,根据最小回路的不同种类进而确定两个多边形的交、并、差。
3.1 最小回路的搜索与种类
对经过转换为单环的两个多边形,确定其边的交点mi(i=1,2,…),以及各交点处关联边序列CElist_mi,从各个交点处沿所有正向边搜索最小回路,遇到交点遵循搜索前进边与当前边沿顺时针方向转角最小的原则。
若多边形P和Q有边相交(含“桥边”),则搜索到的所有最小回路中,每个回路均分别包含P和Q的边,各边在回路中或是逆时针走向或是顺时针走向,但对于同一个多边形P或Q的边而言,其方向一致。因此最小回路中边的方向存在以下三种情形:
情形1:回路中边ei(ei∈P)的方向呈逆时针走向,而ej(ej∈Q)呈顺时针方向;
情形2:回路中边ei(ei∈P)的方向呈顺时针方向,而ej(ej∈Q) 呈逆时针方向;
情形3:回路中所有边均呈顺时针方向。
将最小回路中包含边ei∈P呈逆时针方向的归为P+类,包含边ei∈P呈顺时针方向的归为P-类。
3.2 确定多边形的交、并、差
对两个相交多边形P和Q,归类出其中的P+、P-、Q+、Q-四类最小回路后会发现,所有P+类回路的集合构成了P的内域,Q+类回路的集合构成了Q的内域。由于多边形均初始化为逆时针方向,且在交点处均按顺时针最小转角搜索,因此最小回路所包围的区域均为至少其中一个多边形的内域。亦即P-类回路所围成的区域为Q的内域、P的外域。Q-类回路所围成的区域为P的内域、Q的外域。P∪Q的几何意义为P和Q内域的和,可用(P+)∪(Q+)表示,P-Q的几何意义为P的内域、Q的外域,其余类似。确定两个多边形的交、并、差集的规则如表1所示。

表1 确定P与Q的交、并、差的规则
4 奇异情况处理
存在两个多边形P和Q各边没有交点的奇异情况。若两个多边形为不含孔洞的简单多边形,则只有两种情形:完全分离或者包含。如果多边形P有孔洞,多边形Q无孔洞,满足P的外环P-out⊃Q,则P完全处于Q的內域;满足Q⊂P-in,则P与Q完全分离;其余情况下,P和Q交、并、差集则需视P有多少内环、其中有哪些处于Q内域、哪些处于Q外域的情况而定。如果P和Q均有孔洞则情况更为复杂,其交、并、差集需要视包含所有内外环之间的嵌套关系而定。由于一个多边形可能具有多个孔洞,因此需要对两个多边形的外环和各个内环之间检测包含关系,以此来确定交并差集。两个环的包含关系可通过取一个环上一顶点检测是否位于另一个环内来确定。
5 算法分析与算例
在用时方面,第3小节算法中若多边形P和Q的顶点个数分别为n和m,不妨设n≥m,k为P与Q的交点个数,环路转换过程中,寻找内环最右点时间复杂度不超过O(nlogn),根据文献[6]寻找两个单环的交并差集的时间复杂度为O((n+m+k)logd),其中d为将多边形分为不同的单调链的个数,d<max{m,n}。在奇异情况下,点的包含性检测时间复杂度为O(n)。综上所述,整个算法时间复杂度为O((n+m+k)logd),其中d为将多边形分为不同的单调链的个数,d<max{m,n},与目前较优的文献[8]算法复杂度(O(k(n+m)+O(n+m+k))相当,但避免了文献[8]中大量复杂的反三角函数运算。
在Matlab环境中对两个含孔洞多边形的交、并、差集计算进行了大量测试,试验结果表明算法对各类情况均能有正确的结果,证明了算法的鲁棒性。图4~7为其中四个算例。算例1为含孔洞多边形与不含孔洞多边形相交;算例2为两个含孔洞多边形相交;算例3为两个含孔洞多边形内、外环互相嵌套;算例4为两个含孔洞多边形其中一个完全位于另一个內域和外域的两种情况。
6 结 论
本文给出了基于最小回路方法确定两个含孔洞多边形交、并、差集的方法,通过添加一个双向“桥边”,将多环顶点序列转换为单环,进而利用最小回路法进行布尔运算。扩展了最小回路方法的适用域,将两个任意多边形交、并、差集的计算方法归一为同一个算法,算法适应于重叠边、交于顶点、以及互相包含无交点等奇异情况。算法充分利用了多边形的几何及拓扑信息,降低了算法时间复杂度。试验与分析表明算法具有较高的效率和良好的适应性。
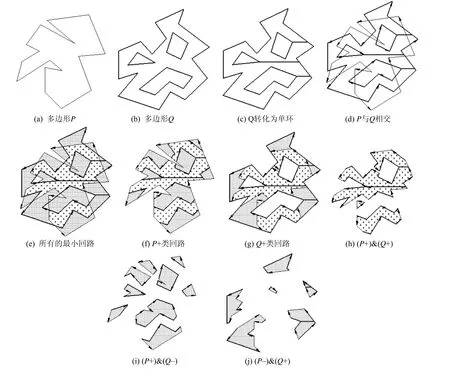
图4 算例1
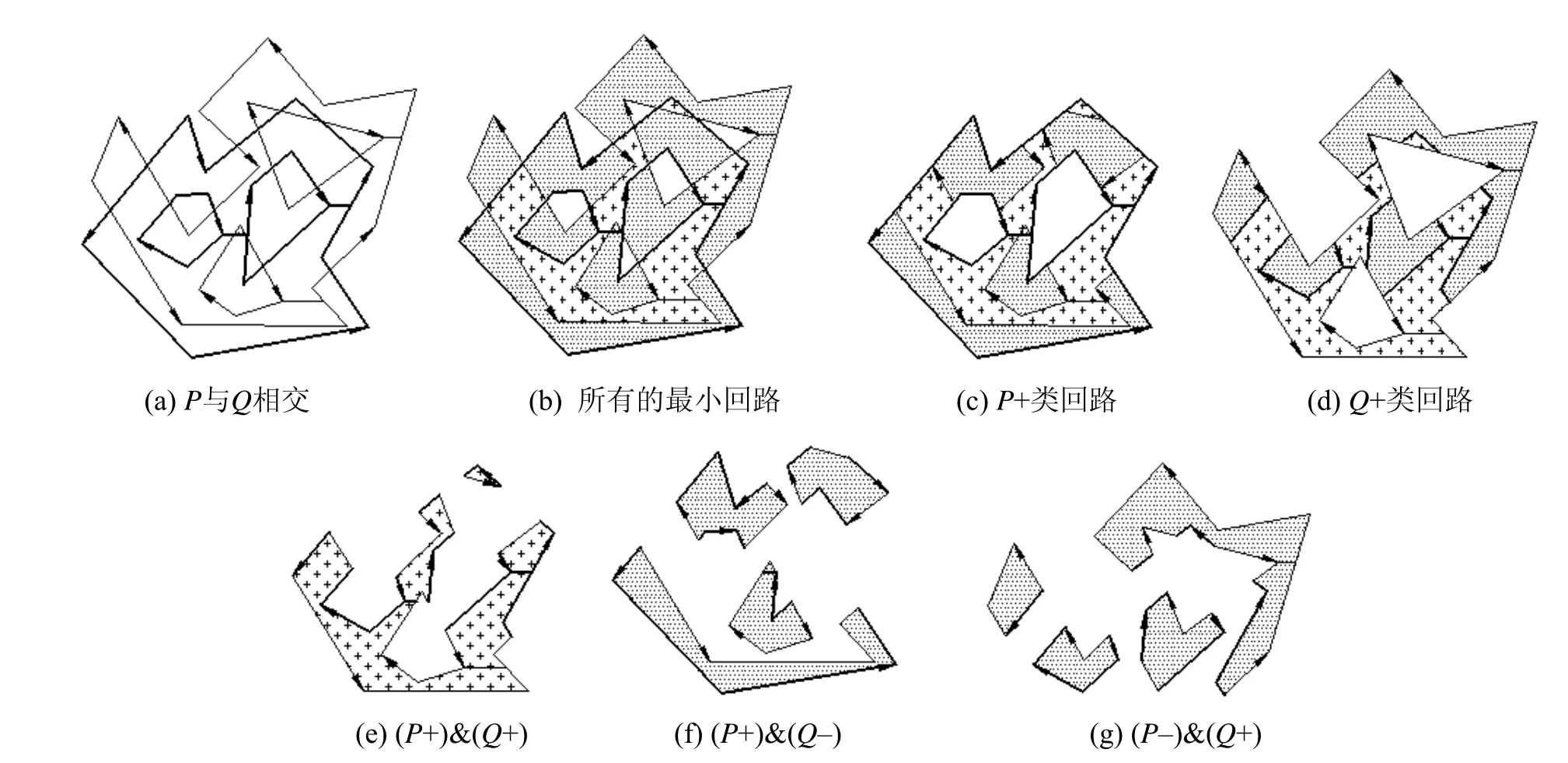
图5 算例2
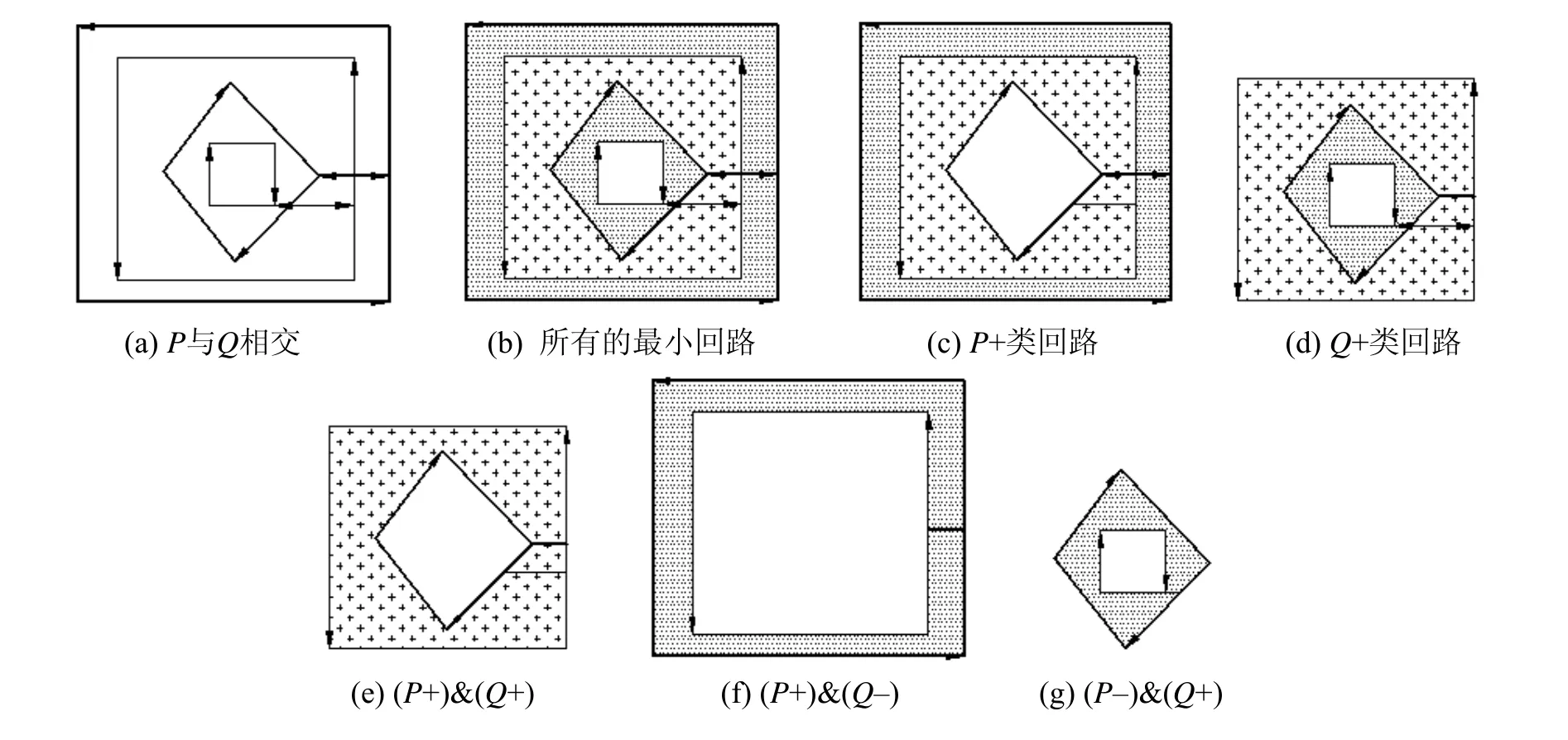
图6 算例3
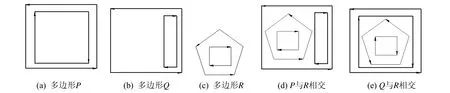
图7 算例4
[1]Feito F R, Rivero M.Geometric modeling based on simplicial chains [J].Computers & Graphics, 1998, 22(5):611-619.
[2]Rivero M, Feito F R.Boolean operations on general planar polygons [J].Computer & Graphics, 2000, 24(6):881-896.
[3]何援军.计算机图形学[M].2版.北京: 机械工业出版社, 2009: 65-79.
[4]董未名, 玛依拉·巴榜, 周登文, 孙家广.平面扩展简单多边形的布尔运算[J].计算机辅助设计与图形学学报, 2003, 15(9): 1134-1140, 1144.
[5]周培德.计算几何——算法分析与设计[M].4版.北京:清华大学出版社, 2011: 238-241.
[6]朱雅音, 王化文, 万 丰, 于雷易.确定两个任意简单多边形交、并、差的算法[J].计算机研究与发展, 2003,40(4): 576-583.
[7]刘红军, 王从军, 黄树槐.带有孔洞的多边形的布尔运算[J].华中科技大学学报(自然科学版), 2003, 31(8):18-20.
[8]朱二喜.基于图形内角的两个任意多边形的交并差算法[D].上海: 上海交通大学, 2009.
[9]崔 璨, 王结臣.一种基于梯形剖分的多边形布尔运算方法[J].测绘学报, 2011, 40(1): 104-110.
[10]赵 军, 刘荣珍.用最小回路求两个简单多边形的交、并、差集[J].计算机应用, 2012, 32(11):3164-3167.
[11]Park S C, Shin H.Polygonal chain intersection [J].Computer& Graphics, 2002, 26(2): 341-350.
[12]刘荣珍, 赵 军, 程耀东.求简单多边形可见点的一种新算法[J].工程图学学报, 2009, 30(2): 109-113.
