光致旋转中晶体微粒厚度对旋转频率的影响
2014-03-20朱艳英肖长江
魏 勇,朱艳英,肖长江
(1.燕山大学里仁学院,河北 秦皇岛066004;2.燕山大学理学院,河北秦皇岛066004)
1 引言
目前,光致旋转技术在微纳米光学机械领域中的研究越来越广泛。激光束在双折射晶体微粒内传播时其偏振态会发生相应的改变,将自旋角动量转移给晶体微粒,从而使其发生自转[1]。光致旋转为光驱动微机械马达技术的实验操作提供了非常有效的帮助,1998年昆士兰大学的Friese等[2]首先实现了CaCO3晶体微粒的光致旋转,并在有效激光功率为7 mW时测出厚度为1μm晶体微粒的旋转角速度。2013年,Kornelia等[3]利用多阵列光镊系统对球状和棒状的金纳米颗粒进行了捕获、旋转以及重新排列成各种图案。目前国外研究人员利用光致旋转技术可以将旋转着的双折射晶体微粒的位置改变,将其移动到一个万字状的微晶体转子周围,带动转子一起转动[4]。另外,光致旋转技术在生物学、临床医学以及微纳米机器人[5-7]的设计上也有比较广阔的应用前景。
本研究组做了大量的关于这方面的研究,首先利用光镊系统实现了碳酸钙晶体微粒的旋转,接着对双折射晶体微粒的旋转频率受其半径的影响进行了理论分析和实验验证[8-10]。在光致旋转实验中晶体微粒的半径可以精确测量,但是发现对于相同半径的CaCO3和SiO2晶体微粒,它们的旋转频率却可能不相等,通过分析,这应该与其厚度有直接的关系。实际上对微粒厚度的研究是非常有必要的,晶体微粒的厚度不同会导致其穿过的激光偏振状态不同,微粒从激光束获得的自旋角动量也就不相等,从而对其旋转频率产生一定的影响。
本文深入讨论了CaCO3和SiO2双折射晶体微粒在激光束自旋角动量的作用下发生旋转的基本理论,在不同激光功率下分别对CaCO3和SiO2晶体微粒的厚度与其旋转频率的关系进行模拟分析,得出了CaCO3晶体微粒和SiO2晶体微粒的旋转频率与其厚度的周期性曲线变化关系,模拟分析和实验结果基本一致。得到的结论对激光驱动微纳米型马达中晶体转子的参数设计有一定的参考价值。
2 理论分析
一束按照直线方向(z轴)传播的激光光束可表示为:
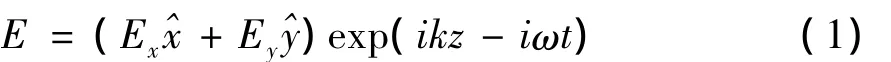
其中,Ex和Ey为复振幅;ω为光的圆频率;为光波矢;λ为波长。双折射晶体微粒的光轴位于x-y平面,其厚度为d;n0和ne分别为双折射晶体微粒的折射率。得出晶体微粒受到的转动力矩为[11]:
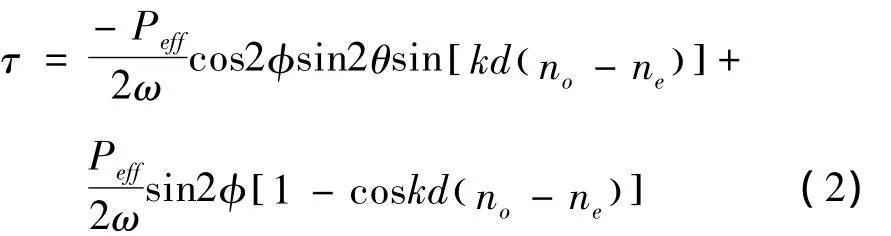
式中,Peff为与晶体微粒相互作用的有效激光功率;θ是x轴与晶体微粒光轴之间的夹角。
旋转着的晶体微粒在溶液中会受到流体的粘滞阻力力矩与其转动角速度Ω成正比关系(比例系数为D)。所以晶体微粒受到的总力矩为:
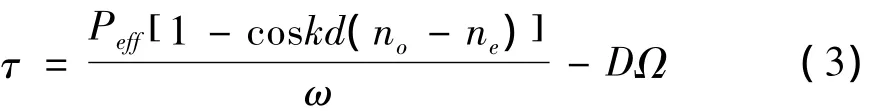
其中,对于圆盘形状的微粒满足[12]D=32ηr3/3,r为晶体微粒的半径,η为溶液的粘滞系数。当阻力力矩和激光束传递给晶体微粒的转动力矩平衡时,晶体微粒的旋转频率保持不变,可得其旋转频率为:
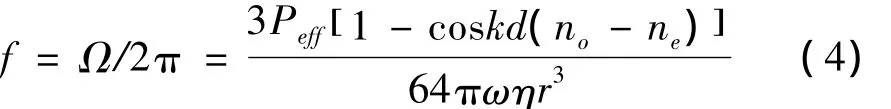

3 仿真分析
所建立的理论模型取值如下:选取入射激光为波长650 nm,有效激光功率分别为10 mW、8 mW和6 mW,实验室温度为25℃时液体粘滞系数 η =0.894 ×10-3N·m-2·s-1,CaCO3晶体折射率为ne=1.6557,no=1.4852,SiO2晶体折射率为 ne=1.5532,no=1.5428。将参数代入式(4)中,然后利用MATLAB软件进行仿真模拟。取晶体微粒半径r=4μm,图1和图2分别表示在6 mW、8 mW和10 mW三种有效激光功率的条件下,CaCO3晶体微粒和SiO2晶体微粒的厚度与其旋转频率的关系曲线。
由图1和图2可以看出,CaCO3和SiO2晶体微
其中,f为旋转频率,则晶体微粒的厚度可由上式得出:粒的厚度与其旋转频率都呈现周期性的正弦曲线变化,并且入射的有效激光功率越大,其旋转频率也会随着提高。图1中当CaCO3晶体微粒的旋转频率达到最大值时,其厚度满足d=1.9×(2n+1)(n=0,1,2,…),而当厚度 d=1.9 × (2n)(n=0,1,2,…)时,会发现无论调节效激光功率为多大,晶体微粒始终不会产生旋转;图2中当SiO2晶体微粒的旋转频率达到最大值时,其厚度满足d=32.5(2n+1)(n=0,1,2,…),而当厚度 d=32.5 × (2n)(n=0,1,2,…)时,晶体微粒的旋转频率为零。所以当微粒达到其最大旋转频率时,Ca-CO3晶体微粒比SiO2晶体微粒的厚度薄。通过以上分析可以得出,在光致旋转实验中可以通过调节合适的激光功率和选择一定厚度的晶体微粒来提高其旋转频率。

图1 功率为6 mW、8 mW和10 mW时CaCO3晶体微粒的厚度与其旋转频率的关系曲线Fig.1 The relationship between rotation frequency of CaCO3 particle and the thickness when laser power are 6 mW、8 mW and 10 mW

4 实验及结果
4.1 实验装置及其操作过程
实验中用到的光学器件有:激光波长为650 nm,输出激光功率0~100 mW的半导体激光器;起偏器、1/2波片和1/4波片等元件;光学显微镜;CCD摄像头以及与四象限探测器等组成的微纳米光学系统。实验光路如图3所示。

图3 实验光路图Fig.3 Experimental optical step
操作的基本过程如下:首先将CaCO3晶体微粒和SiO2晶体微粒分别放在容器内进行反复碾磨,并放置到盛有蒸馏水的瓶内通过电磁振荡以达到实验所需状态[9],静止5~7 min后,瓶中溶液可以作为实验中的晶体微粒溶液样品;其次调节入射光路中加入1/4波片的光轴与线偏振光偏振方向为45°,使得样品溶液中被捕获的CaCO3晶体微粒和SiO2晶体微粒产生转动,此时入射光光束变为圆偏振光,晶体微粒将获得最大的旋转频率,实验现象尤为明显;最后在光镊系统的捕获和操控区域对有效激光功率进行实时测量,并将计算机得到的晶体微粒的旋转情况进行细致分析,进而通过计算可以得到微粒半径和旋转频率等结果。
4.2 实验现象和结果分析
图4为实验系统记录CaCO3晶体微粒旋转一周的过程,旋转方向为逆时针方向。通过大量的实验,从中选取了10个半径为4μm的晶体微粒作为旋转对象,并测量了不同功率下的旋转频率值。表1和表2分别记录了CaCO3晶体微粒和SiO2晶体微粒旋转频率的实验值。

图4 CaCO3晶体微粒逆时针旋转Fig.4 Optical rotation of CaCO3 crystal

表1 CaCO3晶体微粒旋转频率的实验值Tab.1 the experimental data of rotation frequency of CaCO3 particle
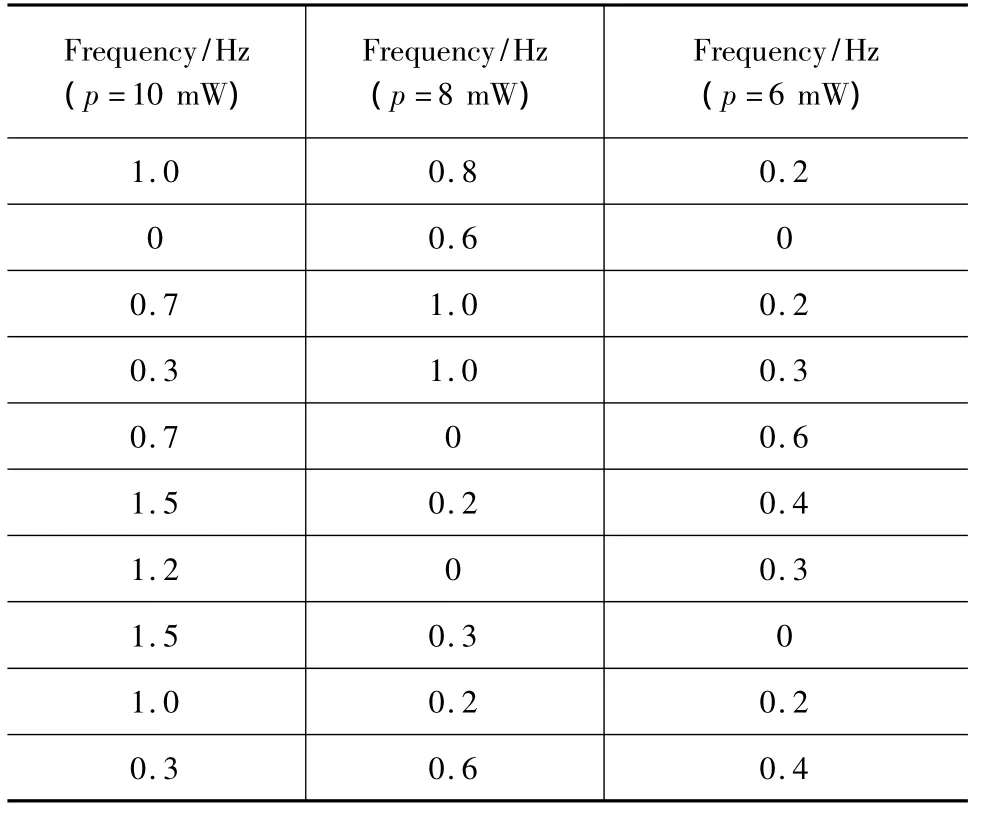
表2 SiO2晶体微粒旋转频率的实验值Tab.2 the experimental data of rotation frequency of SiO2 particle
由表1和表2的实验数据可以得出,在同样的有效激光功率条件下,对于半径相同的晶体微粒其旋转频率一般情况下是不相等的,并且有的差别比较大,同时随着有效激光功率的提高,微粒旋转频率也会随之增大。当入射有效激光功率为10 mW时分别测得CaCO3和SiO2晶体微粒的最大旋转频率为1.7 Hz和1.5 Hz。实验结果与理论模拟是基本一致的。同时会发现,在同一功率下晶体微粒的实验频率值略低于其理论值,分析这是由于溶液中样品的形状可能不是对称的圆盘状,因此光反射和光吸收效应会对其旋转频率产生一定的影响,所建的理论模型还有待进一步的改进和完善。另外,由于晶体微粒的厚度在实验中不能直接测量,只能通过定制不同厚度的微粒来测其旋转频率,所以可以根据式(5),利用测量的晶体微粒旋转频率数值对其厚度作出一个估计值,也可以对实验光路进行重新设计,通过多加一个光源制造光阱从而利用四象限探测器直接对厚度进行直接测量,但是目前实现难度较大。建立在光镊微操控系统之上的光驱动微机械马达设计是以光致旋转技术为基础的,通过以上的实验数据分析可以发现在一定的有效激光功率下,CaCO3晶体微粒的旋转频率较大,并且厚度较薄,因此选用CaCO3晶体微粒作为微机械转子比较合适,根据式(5)其厚度应该选取2μm左右,从而可以有效地提高微机械马达的输出效率。
5 结论
本文根据双折射晶体微粒光致旋转的基本原理,从理论和实验两方面分别对CaCO3和SiO2晶体微粒的厚度对其旋转频率的影响进行了详细的研究,模拟了晶体微粒旋转频率与其厚度的周期性曲线变化关系,并将仿真与实验数据结合进行了分析,给出了晶体微粒在一定厚度下的最高旋转频率,光致旋转技术操控晶体转子的实验研究将在细胞学中鞭毛马达的旋转驱动机理方面有广泛的实际应用。对于形状不规则晶体微粒的光致旋转还有待进一步的研究。
[1] K Dholakia,G Spalding,M Macdonald.Optical tweezers:the next generation[J].PhysicsWorld,2002,10:31 -35.
[2] M E JFriese,T A Nieminen,N R Heckenberg,et al.Optical alignment and spinning of laser-trapped microscopic particles[J].Nature,1998,394:348 -350.
[3] IKornelia,H Marcin,P Bogdan.The new method of fabrication of submicron structures by optical lithography with mask shifting and mask rotation[J].Central European Journal of Physics,2013,11(2):219 -225.
[4] A Sokolov,M M Apodacac,A B Grzybowski,et al.Swimming bacteria powermicroscopic gears[J].PNAS,2010,107(3):969-974.
[5] LILei.Research of activity decay of red blood cells in staticmagnetic field with optical tweezers[J].Laser Technology,2013,37(6):799 -802.(in Chinese)李雷.用光镊研究稳恒磁场对血红细胞的活性影响[J].激光技术,2013,37(6):799 -802.
[6] M N Skryabina,E V Lyubin,M D Khokhlova,et al.Probing of pair interaction ofmagneticmicroparticleswith optical tweezers[J].Jetp Letters,2012,95(11):560 - 564.
[7] W Carolin,O Carsten,B Hergen,et al.DNA condensation by tmhu studied by optical tweezers,AFM and molecular dynamics simulations[J].Journal of Biological Physics,2011,37(1):117 -131.
[8] GAO Qiujuan,ZHU Yanying,SHI Jinshan,et al.Rotation of particles by using the beam with spin angular momentun[J].Chinese Journal of Lasers,2008,35(10):1505 -1510.(in Chinese)高秋娟,朱艳英,史锦珊,等.利用具有自旋角动量的光束实现微粒的旋转[J].中国激光,2008,35(10):1505-1510.
[9] ZHANG Jingchao,ZHU Yanying,DOU Hongxing,et al.Analysis of radius effect on optical rotation of birefringent crystal particles[J].Infrared and Laser Engineering,2012,41(1):156 -159.(in Chinese)张景超,朱艳英,窦红星,等.双折射晶体微粒光致旋转受其半径影响分析[J].红外与激光工程,2012,41(1):156-159.
[10] ZHU Yanying,WEIYong,DOU Hongxing,et al.Effect of ellipse degree of incidence light on rotational angular velocity of the crystal particle[J].Infrared and Laser Engineering,2012,41(12):3406 -3409.(in Chinese)朱艳英,魏勇,窦红星,等.入射光椭圆度对晶体微粒旋转角速度的影响[J].红外与激光工程,2012,41(12):3406-3409.
[11] A T Nieminen,N R Heckenberg,H Rubinsztein - Dunlop.Optical measurement of microscopic torque[J].J.Mod.Opt,2001,48:405 -413.
[12] SUN Yufen,LIYinmei,LOU Liren,et al.Optical rotation of crystal CaCO3micro - particle in optical tweezers[J].Chinese Journal of Lasers,2005,32(3):315 - 318.(in Chinese)孙玉芬,李银妹,楼立人,等.光阱中CaCO3晶体微粒的光致旋转[J].中国激光,2005,32(3):315 -318.
