光阑约束超几何激光束的传输特性

段 旭，唐 斌，周 昕，陈宪锋，蒋美萍，王 帅

(1．常州大学数理学院，江苏 常州213164;2．湖南工业大学理学院，湖南株洲412008)

其中，a为圆孔光阑半径。式(5)可改写为:

1 引言

近年来，随着激光应用领域的不断发展，科学家对新型激光束理论和实验的研究产生了浓厚的兴趣。其中，中心强度为零的暗中空光束由于在原子光学、量子光学、二元光学、微观粒子的操控等方面的广泛应用越来越受到人们的关注。在实验上，有多种方法可以用来产生空心光束，如横模选择法、光学全息法、空心光纤法等［1－3］。在理论上，人们提出了多种模型来描述空心光束，典型的有TEM*01光束、贝赛尔－高斯光束和空心高斯光束［4－6］。最近，Kotlyar提出了合流超几何模式的激光束［7］，该光束复振幅分布正比于合流超几何函数，其横截面光强分布与贝赛尔光束类似，是一系列明暗交替的同心圆环等，随后，Chen等在实验室提出了一种产生超几何激光束的新方法，并研究了其在自由空间近轴光学系统中的传播规律［8］。

在实际的光学系统中，光束的传输总是要受到光阑的限制或约束作用，因此对有光阑约束条件下的光束传输研究是非常有意义的。据我们所知，目前人们已研究了多种光束通过不同光学系统的传输规律［9－10］，但对超几何激光束通过有光阑约束条件下的传输特性，尚未发现有人研究。基于此，本文对合流超几何高斯光束通过具有圆孔形状的硬边光阑的传输特性进行分析，通过把圆孔硬边光阑函数展开为复高斯函数的方法，推导出了超几何激光束通过圆孔光阑的近似解析传输公式，并通过数值计算模拟研究该光束的传输特性。

2 超几何激光束在有光阑约束的ABCD光学系统中的传播

在柱坐标下，超几何激光束在入射面(z=0)的场分布为［7］:

式中，r，()表示柱坐标系统;E0是一个常量;σ代表高斯光束束腰宽度;m是光束参数(可以取任意实数);n是光学拓扑荷(取整数);ω和γ均为实参数。超几何激光束通过近轴有光阑限制ABCD光学系统的传播可以用广义惠更斯－菲涅耳衍射积分的形式表示为:

式(2)中，k是波数，A、B、C和D是近轴光学系统的传输矩阵元。将式(1)代入式(2)，并利用积分公式［11］:

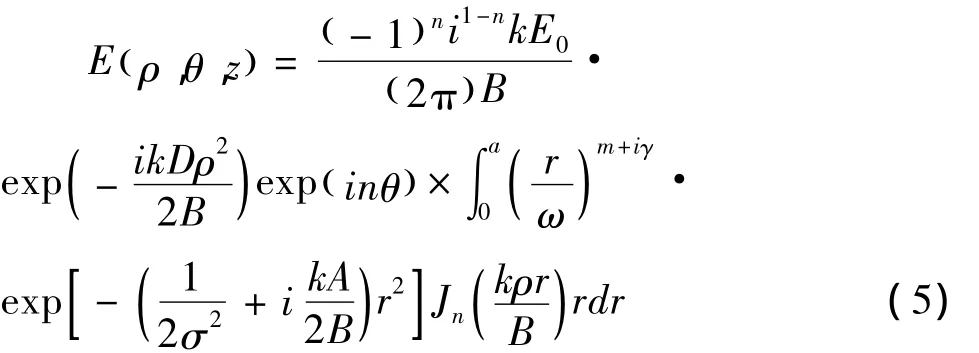
可以得到:

式(3)～式(5)中的J(·)为第一类贝赛尔函数。引入圆孔硬边光阑函数:

其中，a为圆孔光阑半径。式(5)可改写为:

考虑到硬边圆孔光阑函数可拓展为一组复高斯函数之和［12］:

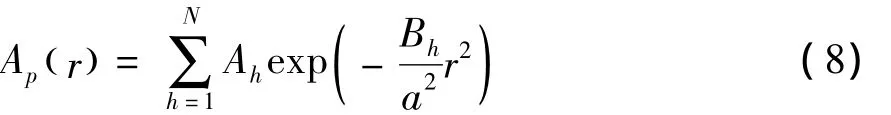
式中，Ah和Bh分别为拓展的复高斯系数。这些系数可以从计算机优化得到。需要指出的是展开项数N越大，拟合精度越高。

将式(8)代入式(7)，并利用积分公式［11］:

式中，1F1(a，b，x)是合流超几何函数或者Kummer函数;Γ(x)是伽马函数。

式(10)即为我们最终得到的超几何激光束通过有圆孔光阑约束条件下的近似解析传输公式，其强度分布可以根据公式 I=来计算。

3 数值计算和分析

由矩阵光学可知，当光束在自由空间传播时，其传输矩阵可表示为:，z为传输距离，在MATLAB环境下，我们利用解析公式(10)，对超几何激光束通过有光阑约束条件下的传输特性进行了数值计算和分析，式(10)中的复高斯系数Ah和Bh取自文献［12］中的表1，这里N取值为10项。

3．1 光阑孔径对光强分布的影响

图1计算了圆孔光阑半径a不断变化的条件下超几何激光束的衍射情况，相关计算参数取值为:z=1000 mm，n=3，m= －1，γ =3，ω =150 mm。为比较近似解析方法和直接数值积分方法的效率，我们给出了两种计算方法的结果，虚线为近似解析方法得到的结果，实线为直接数值积分所得到的结果，除了一些微小差别外，两者结果吻合较好。显然，采用近似解析方法可以大大提高计算效率。此外，从图1不难看出，衍射光强主要集中在主极大附近，光阑半径越小，光强分布范围越宽，即衍射效应越强。当a→∞ 时，光阑效应消失，此时，光强分布形状和无光阑情况一样，这与文献［8］结果基本一致。

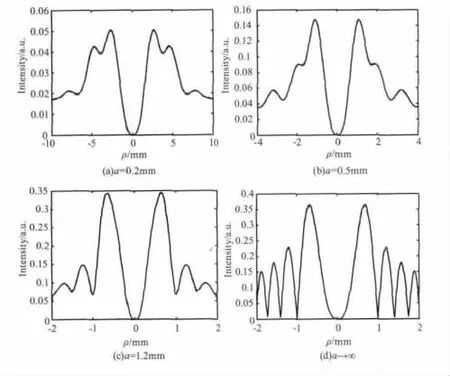
图1 超几何激光束通过不同光阑的衍射强度变化Fig．1 The intensity distribution of hypergeometric beams through different apertures

3．2 不同传输距离对光强分布的影响

基于图1中的数值积分计算和近似解析公式给出的结果，接下来，我们采用近似解析方法来研究超几何激光束在不同传输距离条件下的传输规律。图2描述了传输距离对该光束光强分布特性的影响，考虑到不同光阑的约束作用。图2(a)～(d)同时给出了不同光阑半径情况的光强分布，其中点划线表示光阑半径为0．2 mm，虚线和实线分别表示光阑半径为0．5 mm、1．2 mm。其他参数取值与图1完全相同。从图2不难发现，随着距离的增加，光斑尺寸越来越大，衍射旁瓣减少，主极大和次级衍射条纹光强逐渐变小。

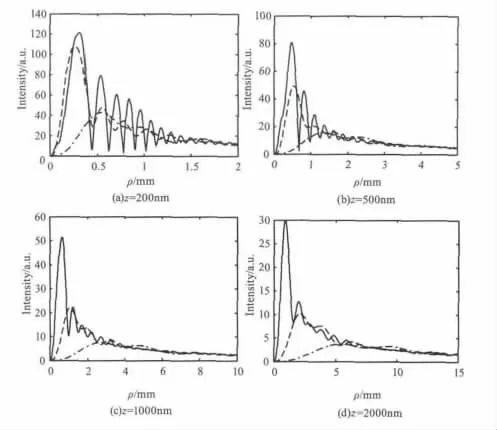
图2 光强分布随传输距离的变化Fig．2 The intensity distribution of hypergeometric beams at the different propagation distances

3．3 不同光束参数对超几何激光束的光强分布影响

图3 描绘了不同光束参数(m，n)对超几何激光束通过圆孔光阑的光强分布影响。在图3(a)中，光束参数m取为定值－1，光学的拓扑电荷数n不断改变，其中实线为 n=3，虚线为 n=2，点线为n=1。从中可以看出，在m固定，n不断减小的时候，衍射光的主极大强度会随着n的减小而减小。同时，各个极大值的位置会逐渐偏离光阑中心位置，极大值的数目不会发生改变。在图3(b)中，光学的拓扑电荷数n取为定值3，光束参数m不断改变，其中实线为m=－1，虚线为m=－1．1，点线为m=－1．2。从中可以看出，在n为定值得时候，随着m不断减小，衍射光束的强度逐渐减小，但是其极大值的位置基本保持不变。

图3 不同光束参数对超几何激光束的光强分布影响计算参数选取为:z=1000 mm，a=1 mm，γ=3，ω=150 mm Fig．3 Effect of the different optical parameters on the intensity distribution of hypergeometric beams．The computation parameters are chosen as follows:z=1000 mm，a=1 mm，γ =3，ω =150 mm

4 结论

采用将圆孔光阑展开为有限个复高斯函数叠加的方法，以及使用广义惠更斯－菲涅耳衍射积分公式，推导出了超几何激光束通过圆形孔硬边光阑约束的ABCD光学系统光强分布的近似解析解，并对其传输特性进行了数值计算和分析。并比较了两种方法得出的结果，发现结果极其相似。从而研究结果表明，超几何激光束的光强分布以及衍射效应与光阑的孔径大小、传输的距离以及光束参数等因素密切相关。事实上，采用本文的研究方法，可以进一步推广到其他光束在其他不同光阑(如环孔、光屏等)约束条件下的传输，并分析和说明光束通过复杂光学系统的衍射特性，这在实际应用中有一定的意义。

［1］ H SLee，BW Atewart，K Choi，etal．Holographic nondiverging hollow beam［J］．Phys．Rev．A，1994，49:4922 －4927．

［2］ R M Herman，T A Wiggins．Production and uses of diffractionless beams［J］．J．Opt．Soc．Am．A 1991，8:932－942．

［3］ SMarksteiner，CM Savage，PZoller，etal．Coherentatomic waveguides from hollow optical fibers:quantized atomic motion［J］．Phys．Rev．A，1994，50:2680 －2690．

［4］ V Balykin，V Letokhov．The possibility of deep laser focusing of an atomic beam into the A － region［J］．Opt．Commun，1987，64:151 －156．

［5］ JArlt，K Dholakia．Generation of high － order Bessel beams by use of an axicon［J］．Opt．Commun，2000，177:297－301．

［6］ Y Cai，X Lu，Q Lin．Hollow gaussian beams and their propagation properties ［J］．Opt．lett，2003，28:1084－1086．

［7］ V V Kotlyar，R V Skidanov，S N Khonina，et al．Hypergeometricmodes［J］．Opt．Lett，2007，32(7):742 － 744．

［8］ JChen，GWang，Q Xu．Production of confluent hypergeometric beam by computer－ generated hologram［J］．Opt．Eng，2011，50(2):024201．

［9］ LIRuxi，ZHAO Chengliang，LU Xuanhui，et al．Propagation properties of the high－order Brssed－Gaussian beam though a circular aperture［J］．Laser ＆ Infrared，2007，37(1):66 －68．(in Chinese)李汝烯，赵承良，陆璇辉，等．高阶贝塞尔－高斯光束通过圆孔硬边光阑的传输特性［J］．激光与红外，2007，37(1):66 －68．

［10］ ZHANG Yongli，PAN Liuzhan．Propagation properties of Bessel beams through a hard－edged annular apertured ABCD optical system［J］．Laser＆ Infrared，2009，39(2):204 －206．(in Chinese)张永利，潘留占．贝塞尔光束通过环形硬边光阑的ABCD 光学系统传输［J］．激光与红外，2009，39(2):204－206．

［11］ A Erdelyi，W Magnus，F Oberhettinger．Tables of integral transforms［M］．McGraw － Hill，1953．

［12］ Wen J J，Breazeale M A．A diffraction beam field expressed as the superposition of Gaussian beams［J］．J．Acoust．Soc．Am．，1998，83(5):1752 －1756．