平面曲线间Hausdorff距离计算

曹利新，董 雷，曹京京

（大连理工大学 机械工程学院，辽宁 大连 116024）

0 引 言

几何对象间距离的计算是工程领域中经常用到的一种几何操作，如几何建模与模式识别中对几何对象的分析与比较［1］；机器人路径规划、CAD／CAM 和触觉仿真中，对物体间的碰撞干涉检测和反馈力的计算［2］.曲线、曲面逼近中构造优化目标和评价逼近程度［3］等众多工程应用领域，都涉及几何对象间距离的计算.在不同的距离测度中，尤以欧几里得最小距离和Hausdorff距离受到几何建模、计算几何和计算机图形学等研究领域学者的格外关注.

几何对象间最小距离的计算问题，就是在两个几何对象间求解对应距离最小的一对点.当需要比较两个对象间的相似程度时，则常采用Hausdorff距离.Hausdorff距离是由现代拓扑学的奠基人之一德国数学家Hausdorff 首先提出［4］，广泛用于衡量两个集合之间差别的度量.早期的Hausdorff距离计算主要出现在模式识别、图像处理领域，为了对两幅图像进行匹配或比较，通常对两幅图像首先进行边缘提取、距离变换等预处理；然后将预处理后的图像像素看作两个集合，通过对两集合间Hausdorff距离的计算，进而对两图像间的相似度进行评价；对其中一幅图像进行仿射变换，使变换后图像与目标模板图像间的Hausdorff距离达到最小，若该距离小于给定的公差，则表示两幅图像获得了匹配，这一方法目前已广泛用于人脸、指纹、字符、笔迹、汽车车牌等的识别［5－6］.

与图像领域中Hausdorff距离的计算和应用研究形成鲜明对比的是，针对连续几何对象间的Hausdorff距离的计算研究则相对较少，截至目前，只有少数学者［1－3，7－8］针对自由曲线或曲面间的Hausdorff距离的精确计算进行过研究.2008年，Alt等［1］证明了两C1连续的平面曲线间单向Hausdorff距离h（A，B）会出现4 种情况，即Hausdorff距离可能发生在：曲线A的一个端点和它在曲线B上的垂足点之间、曲线B的一个端点和它在曲线A上的垂足点之间、双垂足点间、一曲线自身的中线与另一曲线的交点之间，并给出了4种情况分别对应的非线性约束方程组，最终借助标准的代数方程组求解器获得了平面曲线间的Hausdorff距离.同年，Elber等［2］将平面C1连续曲线Hausdorff距离出现4种情况这一结论推广到空间曲线／曲面间，并利用作者自己开发的代数方程组求解器获得了相应的Hausdorff距离，同时以平面曲线为例给出了Hausdorff距离的几何含义：A对B的单向Hausdorff距离，可看作是对曲线B进行等距变换，当曲线A恰好完全包含在曲线B的等距线内时，此时的等距距离为A对B的 单 向Hausdorff距 离.2010 年，Chen等［3］针对文献［1－2］中非线性方程组求根方法的不足，研究了计算两B 样条曲线间Hausdorff距离的几何裁剪方法，算法给出了Hausdorff距离出现在曲线端点的充分条件，利用曲线分割技术和滚动圆裁剪方法，将两曲线的Hausdorff距离计算问题转化为点和曲线的最小或最大距离计算问题，从而提高了算法的稳定性和计算效率.同年，Kim 等［7］针对两平面自由曲线提出了一种精确计算Hausdorff距离的实时算法.首先采用G1连续的双圆弧，在给定公差下对自由曲线进行逼近；进而对这些圆弧进行距离映射并保存到图形硬件深度缓冲器；并对大部分多余的圆弧段进行裁剪，从而提高了Hausdorff距离的计算效率.2011年，Bai等［8］提出了计算平面曲线间Hausdorff距离的折线方法，该方法首先根据给定容差将连续曲线离散为折线段，进而将曲线间的Hausdorff距离计算转化为连续折线段间的Hausdorff距离计算，同时针对无用的折线段给出了两种裁剪策略，极大地提高了这一复杂问题的计算效率.2013年，Ko［9］从理论上深入分析了平面曲线间Hausdorff距离计算的复杂性问题.

综合现有文献来看，针对连续曲线或曲面间的Hausdorff距离计算问题，近年来受到几何建模、计算几何、计算机图形学等领域学者的关注，同时也是Hausdorff距离在工程界获得广泛应用的瓶颈所在.目前的研究工作存在如下问题：（1）针对连续几何对象间Hausdorff 距离计算的研究相对较少，尤其是针对自由曲线或曲面间的Hausdorff距离计算更少；（2）大多学者通过对代数方程组的求解获得Hausdorff距离，并将代数方程组的求解当作了一个黑箱或采用标准求解器求解，未给出太多有参考价值的解算方法；（3）C1连续平面曲线间的单向Hausdorff距离会出现4种情况，由于4种情况对应的非线性方程组并不相同，需要利用代数方程组求解器对4种情况对应的非线性方程组分别进行求解，这将严重影响曲线间Hausdorff距离的计算效率.

本文仅讨论平面连续曲线间Hausdorff距离的计算问题，算法分两步对平面曲线间的单向Hausdorff距离进行计算，最终选择优化结果中的最大值作为两平面曲线间的单向Hausdorff距离.

1 平面曲线间Hausdorff距离对应点的分类

Hausdorff距离分单向和双向两种，对于两个非空的紧致集合A与B，集合A中一个对象相对于集合B中所有对象的最小距离的最大值，称为集合A到集合B的单向Hausdorff距离，表示为

式中：d（a，b）为点a和点b间的欧几里得距离.同理，集合B到集合A的单向Hausdorff距离可表示为

单向Hausdorff距离通常用来表示一个集合相对于另一个集合的最大偏差.两个单向Hausdorff距离中的大者称为集合A与B的双向Hausdorff距离，简称Hausdorff距离，用来表示集合A、B间的最大偏差，亦可用来表示集合A与B的相似度.双向Hausdorff距离通常表示为

从Hausdorff距离的定义可以看出，最小距离的确定是计算Hausdorff距离的基础.由于双向Hausdorff距离与单向Hausdorff距离的算法相似，下面仅进行h（A，B）的计算讨论.

文献［1］对C1连续的平面曲线间可能对应单向Hausdorff距离的点进行如下分类：

A 类端点：即曲线A对曲线B的单向Hausdorff距离h（A，B），出现在曲线A的一个端点和其在曲线B上的法向映射点或曲线B的一个端点处，如图1（a）所示.

B类端点：h（A，B）出现在曲线B的一个端点和它在曲线A上的法向映射点处，如图1（b）所示.

双垂足点：当h（A，B）的对应点发生在两条曲线内部，且对应点为一一对应时，即出现如图1（c）所示的双垂足点情形，因对应点均为垂足点，故称为双垂足点.根据曲线间距离函数取得极值的必要条件，可以将曲线间双垂足点对应的约束方程表示为

图1 平面曲线间Hausdorff距离对应点的分类Fig.1 Hausdorff distance between two planar curves and corresponding points

式中：rA、rB分别表示曲线A、B上对应点的矢径；r′A、r′B分别表示曲线A、B在对应点的切矢.上式表明两曲线在对应点处的切线平行，即存在公法线.

一对二点：当h（A，B）的对应点发生在两条曲线内部，且曲线A上一点对应曲线B上两点时，则出现如图1（d）所示的一对二点情形.一对二点也可以看作是曲线A与曲线B的中轴线的交点，以及中轴变换圆与曲线B的两个切点的总称.一对二点对应的约束方程可表示为

式中：s、t分别为曲线B上两个对应点的曲线参数值；式（5a）表示曲线A上的点N到曲线B上点P和点Q的距离相等，式5（b）、（c）表示向量PN和QN分别与曲线B上P、Q两点处的切线垂直.

从平面曲线间单向Hausdorff距离对应的4种可能点来分析，对于参数曲线，前两种情况均可看作是h（A，B）的对应点的曲线参数为曲线参数域的边界，只有当曲线为开曲线时才会出现这种情况.当h（A，B）的对应点均为各自曲线的内部点，若对应点为一一对应时，则为双垂足点情形；若曲线A上一点对应曲线B上两点时，则为一对二点情形.此时用曲线B的等距线包容曲线A时，等距线自身必发生自交现象，自交点即为点N.上面所讨论的4种情形均是非退化时的情况，若考虑到退化情况会更复杂.例如，一对二点情形中的P点刚好是曲线B上的一个曲率极值点时，此时曲线B上的对应点退化为一个，但又不同于双垂足点情形.

上面给出了平面曲线间单向Hausdorff距离对应的4种类型可能点，对于工程中遇到的实际曲线，曲线上局部满足4种类型点所对应约束条件的点有多个，通常需要分别计算所有可能点，并从中选取最大距离点作为h（A，B）.由于双垂足点和一对二点所对应的约束方程不同，通常需要对曲线A和B分别按照约束方程（4）和（5）进行计算，再从中选取最大值作为曲线A对B的单向Hausdorff距离.这样的计算显然效率并不高，因为同样的步骤，如曲线分段、求解约束方程组等，均需要进行两次计算.为此本文下面分两步对平面曲线间的Hausdorff距离进行计算.

2 曲线间单向Hausdorff距离的近似计算

为了计算曲线A到曲线B的单向Hausdorff距离，本文首先对曲线A进行离散化处理，获取曲线A上的n个离散点.由于仅需要获得两曲线间h（A，B）的近似解，最终的计算精度取决于下一节的精确计算，故离散间隔不必太小.对曲线A的离散化处理可以简单地按照等参数间隔进行，也可考虑曲线A的曲率特点，在曲率较大的位置设置较多的离散点，在曲率较小的位置设置较少的离散点.然后分别计算各个离散点到曲线B的最短距离，选取若干个距离较大，且满足曲线A上相邻点到曲线B的距离呈“小大小”的点对，作为曲线间单向Hausdorff距离的近似解.这样，平面曲线间单向Hausdorff距离的近似计算就转化为点到曲线间最短距离的计算问题.

设平面内一定点P和一条曲线C：r＝r（t），t∈ ［0 ，1］ ，t为曲线的一般参数.点P到曲线C（t）的欧几里得距离可表示为

对距离函数式（6）求导并令其为零，可得距离函数取得极值的必要条件为

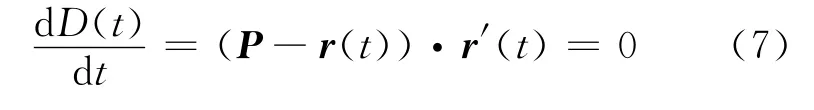
上面距离函数取得极值的必要条件，对应着点P到曲线C局部的距离最大值和最小值.该式表明在距离函数取得极值时，定点P与它在曲线C上的对应点的连线必与曲线C在该点的切矢正交.从所有这些极值中选出最小值，即为点P到曲线C的全局最小距离.问题的关键是如何快速、稳定地求解非线性式（7）.该方程的计算方法通常可以分为局部数值迭代和全局计算方法两大类.局部迭代方法包括常用的牛顿迭代法、二分法、黄金分割法等.局部迭代方法需要为每个根提供较好的初值点，且在有些情况下可能产生振荡，因此很难适用于不便提供初值的多值计算问题.全局计算方法通常有代数与混合技术、同伦方法和细分方法［10］，其中细分方法由于其在多值问题、稳定性和效率方面的优点，受到国内外学者的广泛关注.本文采用细分方法计算点到曲线间的最短距离.

细分方法起源于通过多边形割角（corner cutting）获得光滑曲线的朴素思想，Chaikin［11］在1974年Utah大学举行的CAGD 国际会议上给出了一种基于割角思想快速生成曲线的算法.之后Riesenfeld和Forrest从理论上证明了这种细分极限曲线的数学本质是均匀二次B样条曲线，由此揭开了均匀B样条与细分这个新兴理论的联系［12］.

此处，曲线C采用Bezier形式.若曲线为B样条、NURBS或其他参数多项式曲线，均可转化为Bezier曲线形式.设曲线C为n次Bezier曲线，其表达式为

式中：多项式系数bi为控制点；Bi，n（t）为Bernstein基函数；Cin为组合数；t为曲线参数.

曲线C关于t的一阶导数可表示为

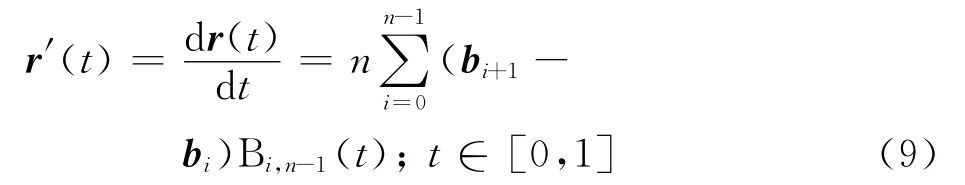
将式（8）、（9）代入式（7），由文献［10］，可得

式（9）、（10）表明，Bezier曲线的一阶导数，以及两个Bezier曲线的乘积仍为Bezier曲线，只是该多项式曲线的次数和系数（即控制点）发生了变化.将式（10）简写为

式中：m＝2n－1；ci＝由于Bernstein多项式具有线性精度特性，式（11）中的参数t可以表示为系数在［0，1］上均匀分布的m次Bernstein多项式的加权和，即

以参数t为水平轴，函数f（t）为垂直轴，则可构造出如下曲线：

式中：（i／mci）T为控制点.

至此，多项式求根问题即转化为一个Bezier曲线与其参数轴求交这样一个几何问题.本文采用文献［10］中的PP 算法对式（13）进行求解，该算法主要依赖于Bernstein形式的多变元多项式细分算法和二维点集的凸壳算法，算法主要包含如下3个步骤：

①首先需要构造Bezier曲线的凸壳，并计算凸壳与参数轴的交点；

②利用de Casteljau 细分算法，剔除参数域中不含有根的区域；

③若剩余的参数域足够小，则返回该参数作为一个根.若经多次剔除不含有根的参数域后，参数域仍非足够小，则表明该参数域中包含一个以上的根，需要利用de Casteljau 细分算法将该参数域一分为二后重新返回步骤①.

利用上面点到曲线最短距离的算法，可以获得曲线A上各离散点到曲线B的最短距离.选择其中距离较大，且满足曲线A上相邻点到曲线B的距离呈“小大小”的点对作为近似解.

3 曲线间Hausdorff距离的精确计算

将前面获得的若干距离较大，且满足曲线A上相邻点到曲线B的距离呈“小大小”的点对作为初始点，根据初始点附近曲线的形状与位置特点，构造相应的Hausdorff距离的精确算法.如图2所示，设P、Q分别为曲线A和B上的关于h（A，B）的一组对应点，假设前面对曲线A的离散化处理遵循数据采样中的采样定理［13］，则精确的Hausdorff距离对应点一定会出现在初始解附近，并随着两曲线的形状与位置不同，表现出多种形式：双垂足点、一对二点、A 类端点和B 类端点，下面分别讨论这4种情形.

图2 双垂足点的计算Fig.2 Computation of antipodal points

3.1 双垂足点的计算

双垂足点包含两曲线间距离的局部最大值和最小值所对应的点对，由于前面的初步计算中仅选取了距离较大的点作为初始点，此处不会出现最小距离所对应的双垂足点.如图2所示，点P、Q分别为曲线A、B上近似的Hausdorff距离对应点对，t、s分别为曲线A、B的参数.P1（t1）、P2（t2）为曲线A上点P的左右相邻离散点，T1、T2为两点处曲线的单位切矢，Q1（s1）、Q2（s2）为它们在曲线B上的最短距离对应点，且满足“小大小”约束所对应的不等式：P1Q1≤PQ≥P2Q2.R1＝P1－Q1、R2＝P2－Q2为两曲线上对应点间的矢量，α1、α2分别为矢量R1、R2与矢量T1、T2之间的夹角，从图2可以看出α1和α2中一个为锐角，另一个为钝角.若Q1和Q2两点间的距离Q1Q2或它们的参数间隔小于某个预先设定的常数，则可认为曲线A、B间单向Hausdorff距离的对应点为双垂足点.以P1、P2两点的曲线参数t1、t2为初值，构造函数

由于f1·f2＜0，可通过二分算法来计算两曲线间精确的局部最大距离所对应的双垂足点.

3.2 一对二点的计算

参考图3，若点P、Q分别为曲线A、B上近似的Hausdorff距离对应点对，且其邻近离散点满足不等式P1Q1≤PQ≥P2Q2约束，但Q1和Q2两点间的距离Q1Q2或它们的参数间隔Δs大于预先设定的常数，则可认为曲线A、B间Hausdorff距离的对应点为一对二点.仍以P1、P2两点的曲线参数t1、t2为初值，构造函数

式中：sgn［x］为符号函数，根据x的正负取“＋”或“－”；d11、d12为点P1到曲线B的最短和次最短距离；d21、d22为点P2到曲线B的最短和次最短距离.由于f1·f2＜0，可通过二分算法来计算两曲线间精确的局部最大距离所对应的一对二点.最终精确的Hausdorff距离的对应点一定会表现为曲线A上的一个点P对应曲线B上的两个垂足点Q1、Q2，且PQ1＝PQ2.

图3 一对二点的计算Fig.3 Computation of intersection point between one curve and self－bisector of other curve

3.3 A 类端点与B类端点的计算

若曲线A或B为开曲线，最终的Hausdorff距离可能发生在曲线的端点.为此，可直接利用第2章关于点到曲线最短距离的算法，计算开曲线的两个端点到另一曲线的最短距离.至此，利用本章算法可实现平面曲线间Hausdorff距离计算中出现的各种形式点的精确计算，与第2章算法结合，则可形成平面曲线间Hausdorff距离的完整算法.

4 数值算例

通过两个算例来验证上述算法的可行性.

例1 曲线A为Bezier开曲线；曲线B为三次均匀B 样条表示的封闭曲线，控制点个数为90.现在要计算曲线A到B的单向Hausdorff距离h（A，B）.计算过程分两个步骤：首先进行h（A，B）的近似计算，将曲线A按照其参数进行均匀十等分离散化处理，利用文献［14］的算法将曲线B由B 样条形式转换为三次分段Bezier曲线，然后利用第2章的方法计算各离散点到曲线B的最短距离；从11 个最短距离中选取距离较大，且满足“小大小”特点的点，利用第3章的算法进行Hausdorff距离的精确计算，计算精度为10－10.计算结果如图4所示.图4（a）给出了曲线A上的11个离散点，以及与第2个离散点对应的曲线B上的14个距离极值点；图4（b）给出了曲线A上11个离散点中与曲线B最小距离较大，且满足“小大小”特征的两个点和曲线B上对应的垂足点；图4（c）表达了经过Hausdorff距离的精确计算后对应点的分布，两个距离分别为66.019 839mm 和54.720 453mm，开曲线A的两端点到曲线B的最短距离分别为27.011 021 mm 和13.104 928mm；对图4（c）中的两个距离以及开曲线的两端点到曲线B的最短距离进行比较，最后的单向Hausdorff距离为66.019 839 mm，对应点如图4（d）所示.

例2 曲线A、B均为立方均匀B 样条表示的封闭曲线，控制点个数均为90，计算精度为10－10.现在要计算曲线A到B的单向Hausdorff距离h（A，B）.计算过程与例1相同，计算结果如图5所示.图5（a）给出了曲线A上的90个离散点，以及第20个离散点对应的曲线B上的10个距离极值点；图5（b）给出了曲线A上90个离散点中与曲线B最小距离较大，且满足“小大小”特征的前三个点和曲线B上对应的垂足点；图5（c）表达了精确Hausdorff距离的计算结果，其中包含一个双垂足点和两个一对二点，3个距离（按红绿蓝 顺 序）分 别 为77.874 235、70.736 729 和66.611 425mm；对图5（c）中的3个距离进行比较，最后的单向Hausdorff距离为77.874 235 mm，对应点如图5（d）所示.

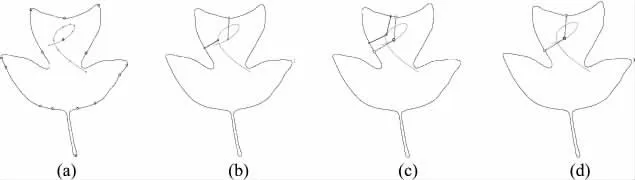
图4 开曲线与封闭曲线间的Hausdorff距离计算Fig.4 Computation of HD between an open curve and a closed curve

图5 两封闭曲线间的Hausdorff距离计算Fig.5 Computation of HD between two closed curves

5 结 论

（1）本文分两步对平面曲线间单向Hausdorff距离进行计算.第一步将其中一条曲线进行离散处理，并计算各离散点到另一条曲线的最小距离，从中选择若干个距离较大且满足“小大小”特征的点对，作为近似的Hausdorff距离对应点；第二步以各近似点对作为初值，依据各点处曲线的特点，建立相应的局部优化模型并求解，从而获得平面曲线间精确的Hausdorff距离.该方法克服了传统的针对4种情况分别求解不同非线性方程组的缺点，简化了计算过程.

（2）通过近似和精确计算单向Hausdorff距离的两步算法，将平面曲线间Hausdorff距离的计算转化为点到曲线的最小距离计算问题；同时利用细分算法可以快速、稳定地获得点到曲线的最短距离，提高了计算效率和稳定性，数值算例验证了本文所提方法的正确性.

［1］ Alt H，Scharf L.Computing the Hausdorff distance between curved objects［J］.International Journal of Computational Geometry ＆ Applications，2008，18（4）：307－320.

［2］ Elber G，Grandine T.Hausdorff and minimal distances between parametric freeforms inR2andR3［J］.Lecture Notes in Computer Science，2008，4975：191－204.

［3］ Chen X D，Ma W Y，Xu G，etal.Computing the Hausdorff distance between two B－spline curves［J］.Computer－Aided Design，2010，42（12）：1197－1206.

［4］ Scholz E.Felix Hausdorff and the Hausdorff edition［J／OL］.［2012－12－09］.http：／／www.math.uni－wuppertal.de／～scholz／preprints／ENLbioHaus.pdf.

［5］ Huttenlocher D P，Kedem K.Computing the minimum Hausdorff distance for point sets under translation［C］／／SCG′90Proceedings of the Sixth Annual Symposium on Computational Geometry.New York：ACM，1990：340－349.

［6］ Huttenlocher D P，Klanderman G A，Rucklidge W J.Comparing images using the Hausdorff distance under translation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1993，15（9）：850－863.

［7］ Kim Y J，Oh Y T，Yoon S H，etal.Precise Hausdorff distance computation for planar freeform curves using biarcs and depth buffer［J］.The Visual Computer，2010，26（6－8）：1007－1016.

［8］ Bai Y B，Yong J H，Liu C Y，etal.Polyline approach for approximating Hausdorff distance between planar free－form curves ［J］.Computer－Aided Design，2011，43（6）：687－698.

［9］ Ko K.On the complexity of computing the Hausdorff distance ［J］.Journal of Complexity，2013，29（3－4）：248－262.

［10］ Patrikalakis N M，Maekawa T.Shape Interrogation for Computer Aided Design and Manufacturing［M］.New York：Springer，2001：73－108.

［11］ Chaikin G M.An algorithm for high speed curve generation ［J］.Computer Graphics and Image Processing，1974，3（4）：346－349.

［12］ 李保军.指数多项式曲线细分重构与插值细分曲面快速计算［D］.大连：大连理工大学，2009.LI Bao－jun.Construction of exponentials reproducing subdivision schemes and rapid evaluation of interpolatory subdivision surfaces［D］.Dalian：Dalian University of Technology，2009.（in Chinese）

［13］ Castleman K R.Digital Image Processing［M］.New Jersey：Prentice－Hall，1996.

［14］ Piegl L，Tiller W.The NURBS Book［M］.2nd ed.Berlin：Springer，1997：142－228.