一类具有混合时滞的神经网络指数稳定性分析

郭良栋，庞 豹，何希勤，贺建军＊2

（1.辽宁科技大学 理学院，辽宁 鞍山 114051；2.大连民族学院 信息与通信工程学院，辽宁 大连 116600）

0 引 言

近年来，人工神经网络被广泛应用于信号处理、模式识别、联想记忆等诸多领域［1－3］.在实际应用中，一般要求设计的神经网络模型必须是稳定的.而时滞的存在往往导致神经网络不稳定.因此，时滞人工神经网络的稳定性分析已经引起了国内外众多学者的极大关注，并得到了大量优秀的成果［4－17］.

为了降低稳定性条件的保守性，文献［4－6］利用积分不等式或积分等式方法，文献［7］通过构造新的Lyapunov－Krasovskii泛函，文献［8－9］使用自由权矩阵的方法，文献［10－11］运用时滞分解方法并构造新的Lyapunov－Krasovskii泛函，分别得到了一系列的稳定性条件.但是，以上得到的结果仍有改进的空间.如文献［10－11］将时滞区间［0，d］分成若干相等的部分，对时滞信息的获得有一定的保守性.

本文进一步讨论具有混合时滞的人工神经网络的指数稳定性问题.通过将离散时滞区间［0，d］分成［0，d1］和［d1，d］两段不等的区间（其中d1∈（0，d）），进一步运用积分不等式与改进的凸优化方法——倒数凸引理［12］来处理Lyapunov－Krasovskii泛函中的积分项，以期克服相关文献时滞分解方法的保守性.

1 系统描述

考虑如下具有分布时滞的人工神经网络：

其中：z（t）＝（z1（t） …zn（t））T∈Rn，为神经元 状 态 向 量，g（z（t）） ＝（g1（z1（t）） …gn（zn（t）））T∈Rn，为神经元激活函数；u＝（u1…un）T∈Rn，是常值输入向量；C＝diag｛c1，…，cn｝＞0；A∈Rn×n，是连接权矩阵；B，D∈Rn×n是时滞连接权矩阵；d（t）、τ（t）为满足0≤d（t）≤d，0≤τ（t）≤τ，（t）≤u的连续时变函数，其中d、τ、u都是常数.初始向量Φ（t）是有界的且在［－h，0］上连续可微，其中h＝max｛d，τ｝.神经元激活函数gi（·）（i＝1，2，…，n）满足

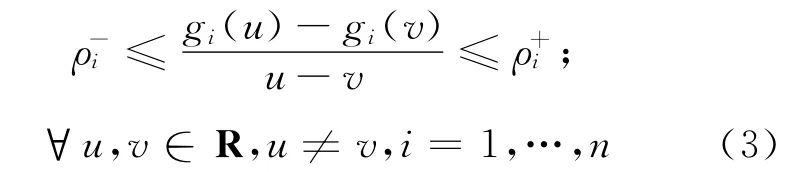
根据Brouwer不动点定理，神经网络（1）存在平衡点.假定z＊＝（z＊1…z＊n）是神经网络（1）的一个平衡点，由文献［13］知该平衡点是唯一平衡点.通过坐标平移变换x（·）＝z（·）－z＊（·），系统（1）转换为如下形式：

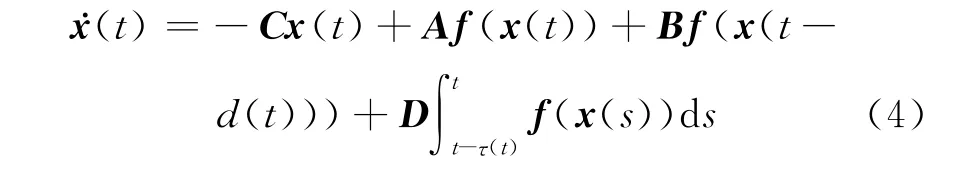
其 中x（t）＝（x1（t） …xn（t））T，f（x（t））＝（f1（x1（t）） …fn（xn（t）））T，fi（xi（t）） ＝gi（xi（t）＋z＊i）－gi（z＊i）（i＝1，2，…，n），且fi（0）＝0（i＝1，…，n）.由不等式（3），可得

当v＝0时，有

定义1 若变量k＞0，β＞0且满足

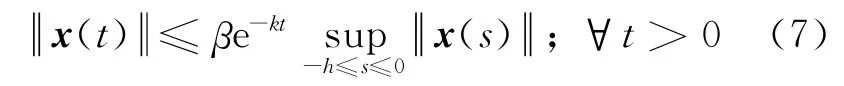
则系统（4）是全局指数稳定的.

引理1［14］对于任意正定矩阵Z∈Rn×n（Rn×n表示n×n的实矩阵），标量h2＞h1＞0，有以下不等式成立：

引理2［12］设f1，f2，…，fN：RmaR 是定义在Rm（Rm表示m维Euclidean空间）的子集D上的正值，则关于fi的倒数凸组合，如果有

则满足

引理3［15］以下不等式成立：

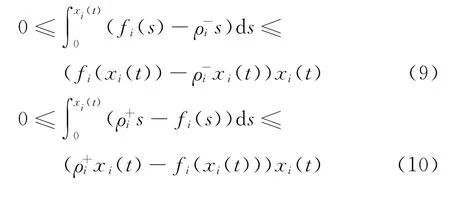
2 指数稳定新判据

下面将给出一个基于时滞分段方法的具有更小保守性的指数稳定性新判据.为了描述方便，记

定理1 对于给定的常数d、d1、τ、u及指数衰减率k，对角矩阵ρp＝diag｛ρ－1，…，ρ－n｝，ρm＝diag｛ρ＋1，…，ρ＋n｝，系统（4）是全局指数稳定的，如果 存 在 对 角 矩 阵K＝diag｛k1，…，kn｝，L＝diag｛l1，…，ln｝，Hi＝diag｛hi1，…，hin｝（i＝1，2，3），n维正定对称矩阵P、Q、Q1、Q2、Q3、Q4、R1、R2、R3、Q11、Q22，n维的矩阵Q12、T1、T2，满足下面的线性矩阵不等式

其中P≥（＜）0表示P为半正定（负定）矩阵，

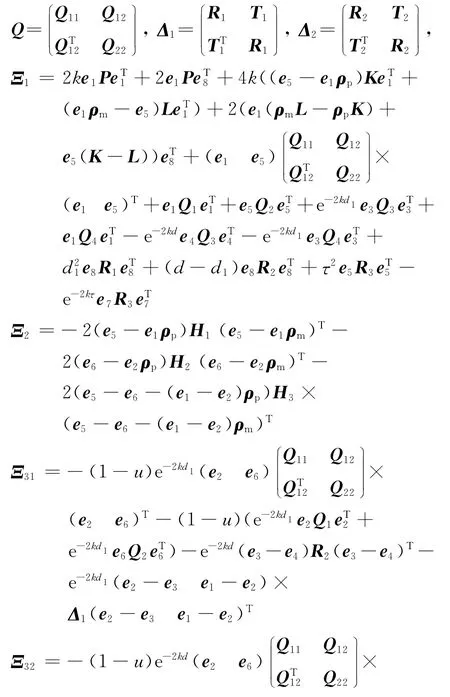
证明 构造如下Lyapunov泛函：

其中

计算Vi（x（t））（i＝1，…，5）的导数，有

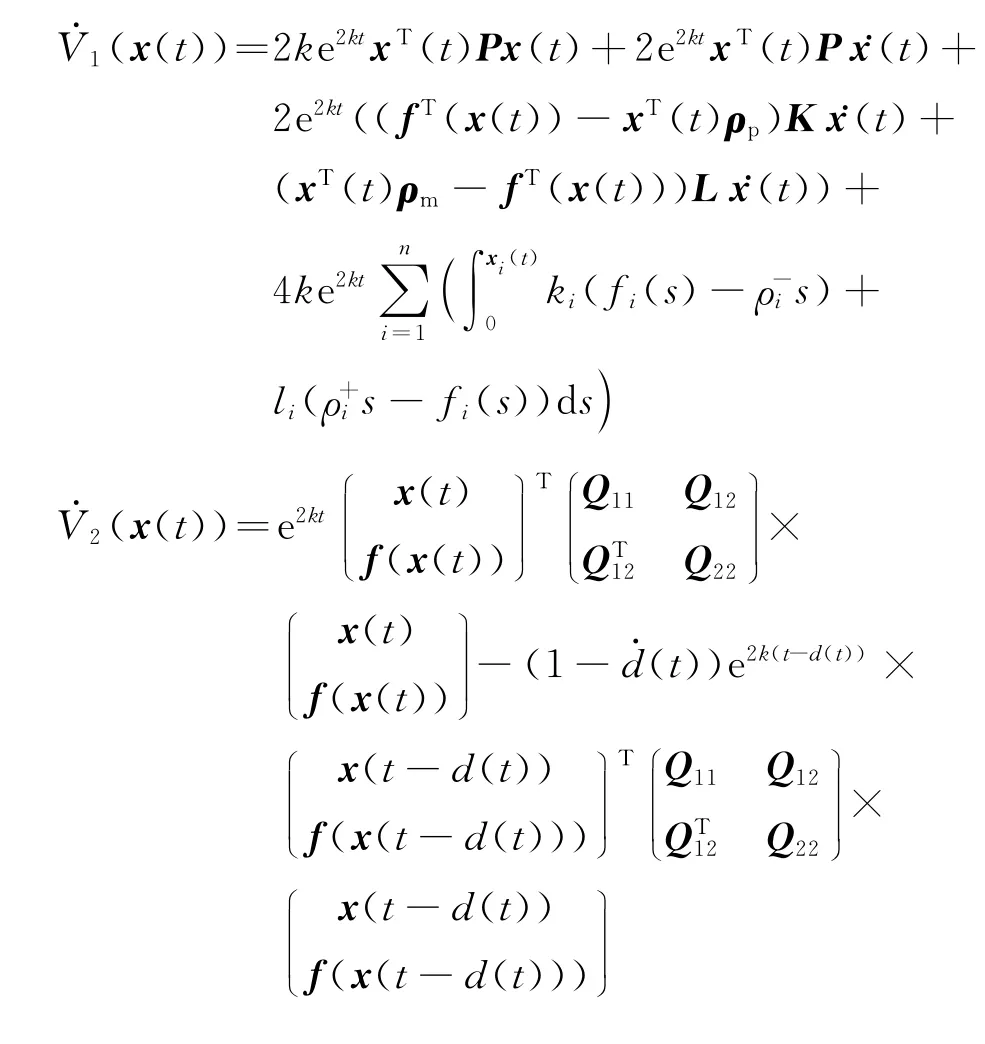
另外，由式（5）、（6）知，对任意的正定对角矩阵Hi＝diag｛hi1，…，hin｝（i＝1，2，3），有

注意到（t）≤u，利用式（8）～（10）以及引理2处理上述导数项中的积分项，将代入所求得的导数中，得

当时滞d（t）∈［0，d1］时

当时滞d（t）∈［d1，d］时

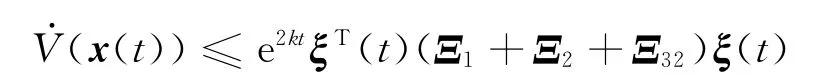
因此，当线性矩阵不等式（11）、（12）成立时，（x（t））＜0，则系统（4）是全局渐近稳定的.

由（x（t））＜0可得，V（x（t））≤V（x（0））.

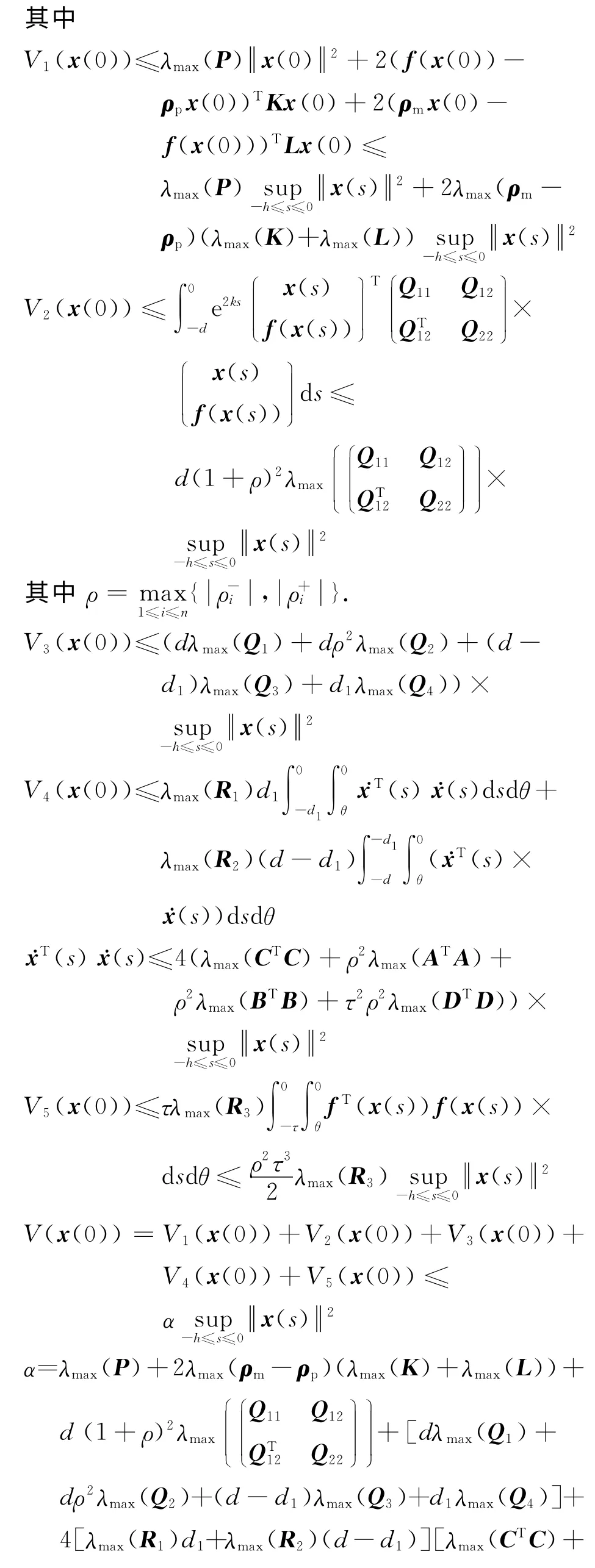
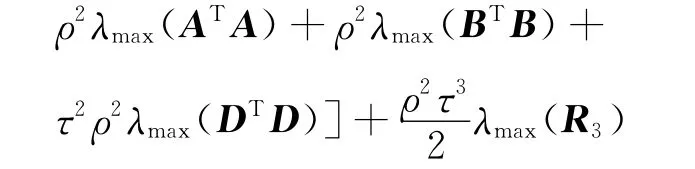
又V（x（t））≥e2ktλmin（P）x（t）2，故x（t） ≤

由定义1可知，系统（4）是指数稳定的，定理成立.证毕.

3 数值实例

下面给出两个数值实例说明定理所给条件的优越性.

例1 考虑系统（4），其中

表1给出了当指数衰减率k＝0，u未知，d＝τ时，利用定理所得时滞上界与文献［11，15－17］的比较，其中文献［15－17］不划分区间，文献［11］均分区间，本文以d1＝5.21划分区间.由表1可以看出，定理所得结果具有更小的保守性.为了验证所得结果，取f（x（t）） ＝1.5cos2t，图1为例1中系统的仿真曲线图.由图1可以看出，当时间逐渐增加时，状态响应曲线趋向于0.

表1 系统稳定的最大时滞上界dTab.1 Allowable delay upper bound d

图1 例1中x1（t）、x2（t）、x3（t）的状态响应曲线Fig.1 State responses curves of x1（t），x2（t）and x3（t）in Example 1

例2 考虑系统（4），其中

当参数τ、u、d为变量时，表2给出了由定理所得的最大指数衰减率与文献［11，15，17］所得结果的比较.由表2可以看出，本文所得结果与上述文献相比有了很大的提高，因此使得指数稳定性结果具有更小的保守性.为了验证所得结果，取0.25sin2t，τ（t）＝0.2cos2t，图2即为例2中系统的状态响应曲线.由图2可以看出，随着时间的增加状态响应曲线也逐渐趋向于0.

表2 在不同的τ、u、d 下，系统稳定的最大指数衰减率kTab.2 Allowable exponential convergence rate index k with differentτ，uand d

图2 例2中x1（t）、x2（t）、x3（t）的状态响应曲线Fig.2 State responses curves of x1（t），x2（t）and x3（t）in Example 2

4 结 语

本文讨论了具有分布时滞的人工神经网络的指数稳定性问题.通过对时滞区间进行不等分割并运用倒数凸引理得到了基于线性矩阵不等式的全局指数稳定性新判据.数值实例说明了所得结果的有效性与更小的保守性.在后续的研究中，将讨论将时滞区间分为不等的3个子区间时，对神经网络稳定性的影响.

［1］ Wong K B，Selvi Y.Neural network applications in finance：A review and analysis of literature（1990－1996）［J］.Information ＆ Management，1998，34（3）：129－139.

［2］ Joya G，Atencia M A，Sandoval F.Hopfield neural networks for optimization：study of the different dynamics［J］.Neurocomputing，2002，43（1－4）：219－237.

［3］ LIU Yu－rong，WANG Zi－dong，Serrano A，etal.Discrete－time recurrent neural networks with timevarying delays：exponential stability analysis ［J］.Physics Letters A，2007，362（5－6）：480－488.

［4］ ZHANG Huang－guang，WANG Zhan－shan，LIU De－rong.Global asymptotic stability of recurrent neural networks with multiple time－varying delays［J］.IEEE Transactions on Neural Networks，2008，19（5）：855－873.

［5］ WANG Zi－dong，LIU Yu－rong，Fraser K，etal.Stochastic stability of uncertain Hopfield neural networks with discrete and distributed delays［J］.Physics Letters A，2006，354（4）：288－297.

［6］ GUO Liang－dong，GU Hong，WANG Zhe－long，etal.An improved delay－range－dependent robust stability criterion for uncertain stochastic Hopfield neural networks with mixed delays ［J］.ICIC Express Letters，Part B：Applications，2011，3（2）：735－741.

［7］ HUA Chang－chun，LONG Cheng－nian，GUAN Xin－ping.New results on stability analysis of neural networks with time－varying delays ［J］.Physics Letters A，2006，352（4－5）：335－340.

［8］ HE Yong，LIU Guo－ping，Rees D.New delaydependent stability criteria for neural networks with time－varying delay ［J］.IEEE Transactions on Neural Networks，2007，18（1）：310－314.

［9］ HE Yong，LIU Guo－ping，Rees D，etal.Stability analysis for neural networks with time－varying interval delay ［J］.IEEE Transactions on Neural Networks，2007，18（6）：1850－1854.

［10］ MOU Shao－shuai，GAO Hui－jun，QIANG Wen－yi，etal.New delay－dependent exponential stability for neural networks with time delay ［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part B，2008，38（2）：571－576.

［11］ TIAN Jun－kang，ZHONG Shou－ming，WANG Yong.Improved exponential stability criteria for neural networks with time－varying delays ［J］.Neurocomputing，2012，97（15）：164－173.

［12］ Park P，Ko J W，Jeong C.Reciprocally convex approach to stability of systems with time－varying delays［J］.Automatica，2011，47（1）：235－238.

［13］ XU Sheng－yuan，Lam J，Ho D W C，etal.Novel global asymptotic stability criteria for delayed cellular neural networks［J］.IEEE Transactions on Circuits and Systems II：Express Briefs，2005，52（6）：349－353.

［14］ GU Ke－qin.An integral inequality in the stability problem of time delay systems［C］／／Proceedings of the IEEE Conference on Decision and Control.Sydney：Institute of Electrical and Electronics Engineers Inc.，2000：2805－2810.

［15］ ZHU Xun－lin，WANG You－yi.Delay－dependent exponential stability for neural networks with discrete and distributed time－varying delays ［J］.Physics Letters A，2009，373（44）：4066－4072.

［16］ SONG Qian－kun，WANG Zi－dong.Neural networks with discrete and distributed time－varying delays：a general stability analysis ［J］.Chaos，Solitons ＆Fractals，2008，37（5）：1538－1547.

［17］ LI Tao，LUO Qi，SUN Chang－yin，etal.Exponential stability of recurrent neural networks with time－varying discrete and distributed delays［J］.Nonlinear Analysis：Real World Applications，2009，10（4）：2581－2589.