由热学性质获取氩晶体原子间各阶力常数

黄建平，胡诗一

(湖南师范大学计算机部，量子结构与调控教育部重点实验室，长沙410081)

1 引 言

根据晶格动力学理论［1］，原子间相互作用决定了晶体的许多物理性质，因此原子间相互作用的研究是一项非常重要的基础研究，长期以来一直是研究热点. 例如，最近Jäger 等人［2］通过ab initio 方法计算得到了氩原子对相互作用势. 然而，由于氩晶体内原子间相互作用不能等同于氩原子对内原子间相互作用，因此Jäger 等人的计算结果不能准确的反映氩晶体内氩原子之间的原子相互作用的实际情况. 虽然通过拟合热膨胀和比热的实验数据，可以获取晶体中原子间相互作用力常数，但由于现有的比热公式只考虑到和谐势能的贡献［3］，热膨胀系数公式只考虑到三阶非和谐势能的贡献［4］，因此我们根据该思路只能对低温段的热学性质参数进行拟合而得到二阶和三阶力常数. 然而在温度较高情况下，更高阶的力常数对热膨胀和比热的贡献不能忽略，因此有必要首先推导得到包含各阶力常数的热膨胀和热膨胀系数公式，以获取更为全面、准确的晶体内部原子间相互作用信息.

尽管氩晶体缺乏实际应用价值，但由于其晶体结构简单，常被用于验证各种固体理论［5］，因此本文也将以氩晶体作为研究对象. 本文将运用晶格动力学和量子力学定态微扰理论［6］，推导比热和热膨胀系数与氩晶体原子间各阶力常数的关系公式，再根据这些公式对热膨胀系数和比热数据［7］进行拟合，计算出氩晶体原子间各阶力常数，并根据这些力常数还原出氩晶体原子间相互作用势能曲线，并与Morse 势能［5］曲线进行比较.

2 氩晶体的晶格动力学基础

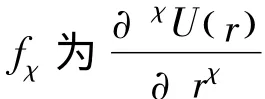
其中，σ、ρ、α 和β 可为x、y 或z，且α、β 和σ互不相同. m 为原子质量，k = ( kx，ky，kz)为格波波矢. 当σ = ρ 时δσρ= 1 ，= 0 ;而当σ ≠ρ时δσρ= 0 ，= 1 .

求解晶格动力学方程［1］，得本征值和对应的本征矢e(kj)，其中，j = 1，2，3，e(kj)满足正交归一化条件. 原子l 围绕平衡位置R( )l 进行简谐振动的瞬时振动位移矢量记为ul( )t . 和谐晶体的晶格原子位移和晶格振动哈密顿可分别表示为其中，N 为原子数，Akj为akj+，和akj是声子的产生与湮灭算符，ħωkj为声子能量，nkj是声子数算符，平均声子数符合玻色统计. 对(3)式求热力学平均，可得和谐晶体的晶格振动内能E2，据此可得比热C2.

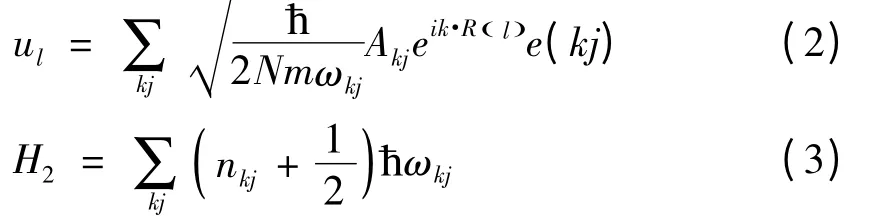
势能中还包含3 阶及3 阶以上非和谐势能项，总的非和谐势能项可表示为

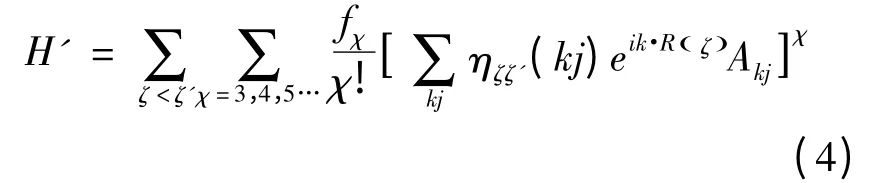
其中，原子ζ 和ζ'互为最近邻原子，ζ ＜ζ'表示对原子ζ 和ζ' 求和时，避免对势能的重复计算. 方括号内为原子ζ 和ζ' 之间距离的变化量.

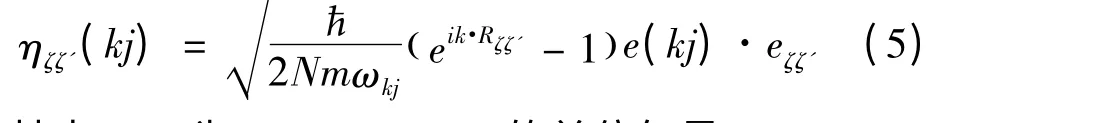
其中，eζζ'为R ζ( )' - R( )ζ 的单位矢量.

3 氩晶体的比热及热膨胀系数公式

非和谐势能较小，在量子力学中可作微扰处理. 在一级近似下，根据量子力学微扰理论，氩晶体晶格振动内能E 可表示为

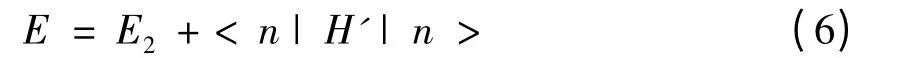
根据(6)式计算可知，在一级近似下，奇次非和谐势能对晶格振动内能没有贡献. 计算到2n 阶非和谐势能，得晶格振动内能

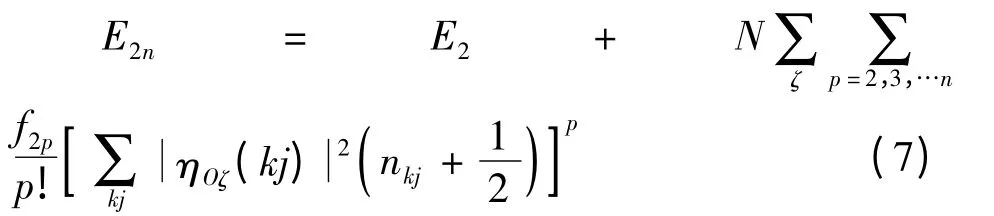
其中，O 为座标原点. 上式可简化为

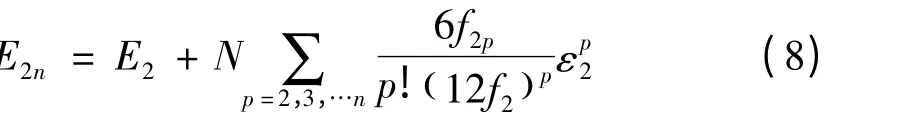
其中，ε2= E2/N 为平均到单个原子的和谐晶体晶格振动内能.

计及至2n 阶非和谐势能对晶格振动内能影响，得到非和谐氩晶体的比热.

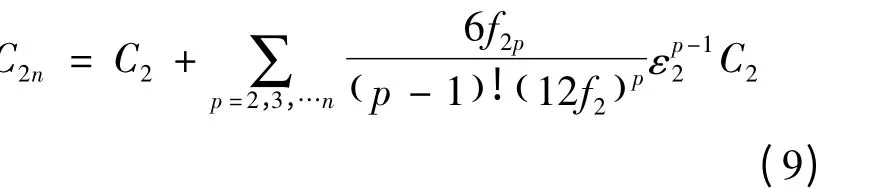
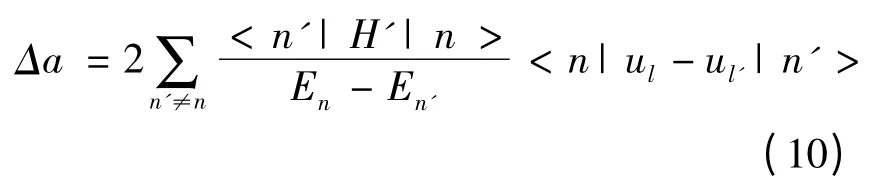
其中，| n ＞或| n' ＞分别是由和谐晶体各种kj 的声子态| nkj＞或| n'kj＞的直积构成的未微扰态.

先计算3 阶非和谐势能项H3对晶格常数热膨胀的贡献Δ3a. 根据(2)式，及声子产生和消灭算符的性质可知， (10)式中求和项非零的条件是| n ＞和| n' ＞状态相差一个声子，设其模为k'j' ，在| n ＞态中该声子的数目为nk'j'，则| n' ＞态中该声子的数目为n'k'j'= nk'j'-1 或n'k'j'= nk'j'+1 ，而所有其它模kj 的声子数在| n ＞和| n' ＞态中是相同的. 根据声子升降算符的性质，以及以上对| n ＞态和| n' ＞态的分析，可知只有当k1j1、k2j2和k3j3中，有一个为k'j'或- k'j' ，另外的为kj 和- kj 时，＜n'| H3| n ＞才不为零.根据以上分析，计算可得

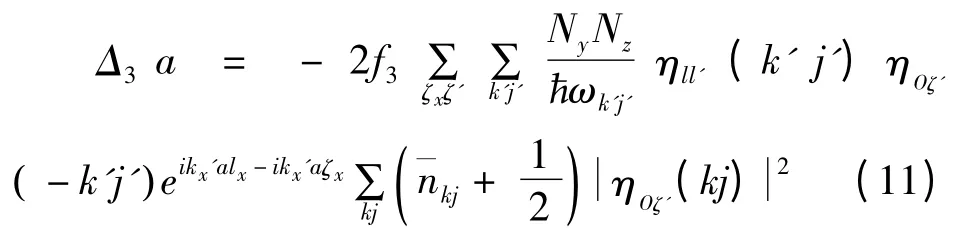
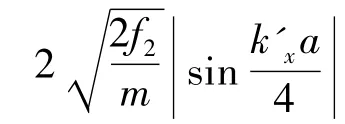
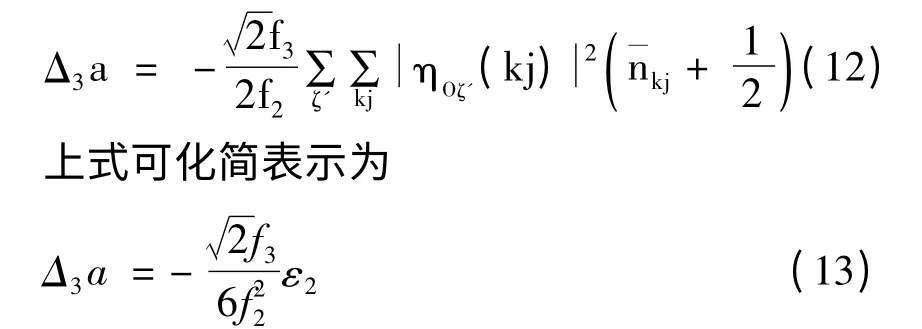
运用以上方法，我们还计算了其它各阶非和谐势能项对热膨胀的贡献，发现只有奇次非和谐势能项对热膨胀才有贡献. 至2n + 1 阶的非和谐势能引起的晶格常数热膨胀为

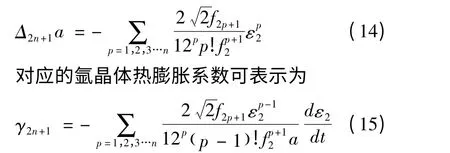
根据(9)式和(15)式可知，比热和热膨胀系数与原子间各阶力常数有关，因而可以利用Peterson 等人［7］的氩晶体比热和热膨胀系数的实验数据计算原子间各阶力常数.

4 数值计算结果与讨论

在低温度区，非和谐势能对氩晶体比热的贡献可以忽略，因此我们首先根据和谐氩晶体比热公式按最小二乘法拟合低温氩晶体比热数据，得二阶力常数，在此基础上计算得到全温区的氩晶体比热与温度的关系曲线，如图1 中的n =2 对应曲线所示.可知，在高温情形，用和谐晶体晶格模型来描述氩晶体的比热性质是有较大误差的，因此必须考虑高偶数阶非和谐势能对比热的贡献. 设n = 12，根据(9)式按最小二乘法拟合全温段的氩晶体比热数据［7］，得到至12 阶的各偶数阶力常数.

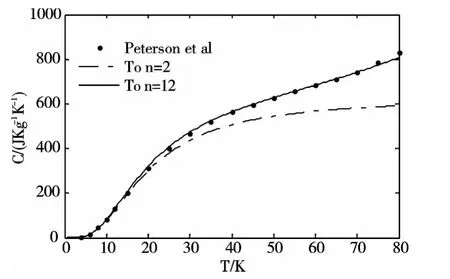
图1 氩晶体比热与温度关系Fig.1 The heat capacity of argon crystal vs temperature

在低温度区，首先只考虑到3 阶非和谐势能，根据(15)式按最小二乘法拟合低温氩晶体热膨胀系数数据，得3 阶力常数，在此基础上计算得到全温区的氩晶体热膨胀系数与温度的关系曲线，如图2 中的n = 3 对应的曲线所示. 可知，在高温区，只计及3 阶非和谐势能对热膨胀性质的贡献也会产生较大误差，必须考虑高奇数阶非和谐势能对热膨胀的贡献. 考虑至11 阶非和谐势能，根据(15)式按最小二乘法计拟合全温段的氩晶体热膨胀系数数据［7］，由此计算出直至11 阶的奇数阶力常数.

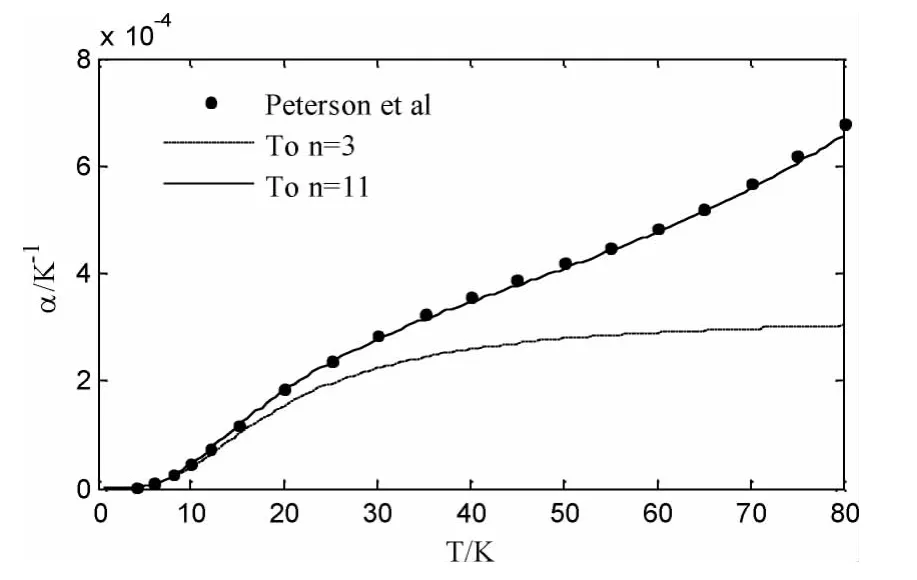
图2 氩晶体热膨胀系数与温度Fig.2 The thermal expansion coefficient of argon crystal vs temperature

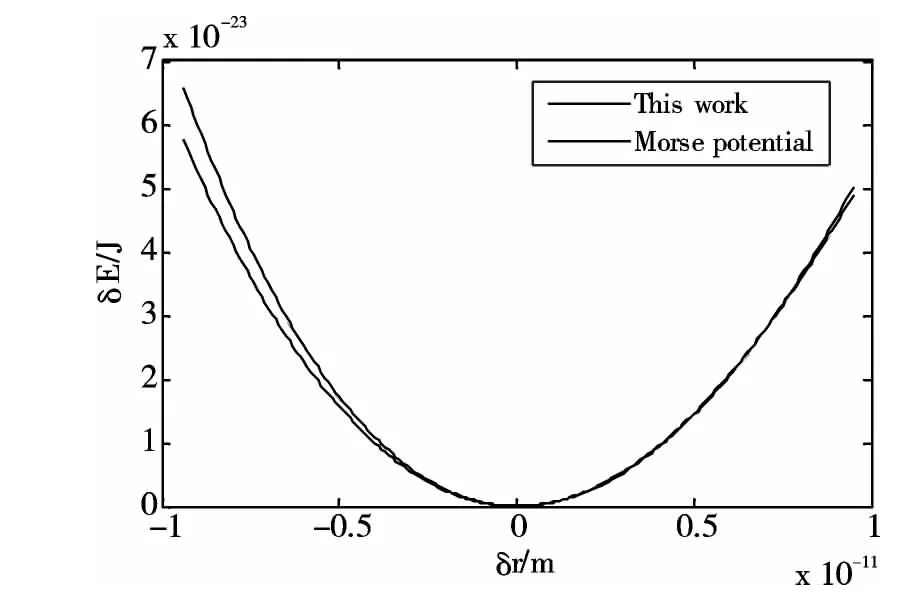
图3 氩晶体中原子间势能与距离变化量关系Fig.3 The interatomic potential of argon crystal vs the change of interatomic space

根据各阶力常数，得到原子间相互作用势能δE 与原子间距离变化量δr 之间的关系曲线如图3所示. 将受Morse 势［5］作用的晶格原子处于平衡位置时的δr 和δE 分别规定为零，绘制得到Morse势能曲线如图3 所示，这与前面得到的势能曲线较好地吻合，说明本文提供的研究氩晶体中原子间相互作用势能的方法和结果是正确和可靠的.

［1］ Bottger H. Principles of the theory of lattice dynamics［M］. Weinheim:Physik-Verlag，1983:15.

［2］ Jäger B，Hellmann R，Bich E，et al. Ab intio pair potential energy curve for the argon atom pair and thermophysical properties of the dilute argon gas.I. Argon -argon interatomic potential and rovibrational spectra［J］. Mol. Phys.，2009，107:2181.

［3］ Mohazzabiy P，Behrooziz F. Thermal expansion of solids:a simple classical model［J］. Eur. J. Phys.，1997，18:237.

［4］ Kittel C. Introduction to solid state physics［M］. 8th Ed. New York:John Wiley ＆ Sons，2005:105.

［5］ Jelinek G E. Properties of crystalline argon，krypton，and xenon based upon the Born - Huang method of homogeneous deformations. III. The low-temperature limit［J］. Phys. Rev. B，1972，5:3210.

［6］ Sakurai J J，Napolitano J. Modern quantum mechanics［M］. 2nd ed. San Francisco:Addison - Wesley，2011:303.

［7］ Peterson O G，Batchelder D N，Simmons R O. Measurements of x-ray lattice constant，thermal expansivity，and isothermal compressibility of argon crystals［J］. Phys. Rev.，1966，150:703.