EPR 核电厂放射性气体释放前运动及延迟滞留状态论证
2014-03-20张学岭陈亦德牛俐珺吕炜枫
张学岭,陈亦德,霍 明,牛俐珺,吕炜枫
(深圳中广核工程设计有限公司,广东 深圳 518172)
在EPR 机组运行过程中,堆芯会产生裂变气体,主要包括Kr和Xe的各种同位素。Kr、Xe等核素的半衰期长短不等。在Kr的同位素中,除85Kr的半衰期相对较长外,其他核素的半衰期一般不超过4h;而Xe的长半衰期同位素为131Xem和133Xe,其 半 衰 期 分 别 达12d 和5.25d。
这些气体可通过燃料包壳的破裂或泄漏进入冷却剂并溶解,溶解有惰性气体的冷却剂会进入与一路回冷却剂系统相连的核岛系统。为确保这些放射性气体向环境释放时满足国家环保要求,EPR 机组配置了放射性废气管理系统,用以控制堆芯产生的裂变气体的运动过程,并提供延迟滞留时间。
本文通过对放射性废气管理系统在稳态运行模式及波动运行模式下气体运动过程进行分析,并建立相关计算模型,论证机组对放射性气体延迟滞留状态的有效性。
1 系统运行模式
EPR 核电厂正常运行期间,放射性废气管理系统有两种不同的运行模式,即稳态运行模式和波动运行模式。
1.1 稳态运行模式
在稳态运行模式下,放射性废气管理系统和与之相联的被服务系统组成一个半闭环回路,由于运行条件改变导致被服务系统及其设备中所含冷却剂中气体的溶解度降低,不溶解的气体进入被服务系统及其设备的气相空间,由氮气吹扫并与一部分泄漏气体共同进入废气管理系统负压部分,经衰变后最终通过烟囱释放[1]。
在该模式下,系统通过压缩机维持微负压并将吹扫气体加压至8×105Pa(g),加压后的气体一部分进入反应堆厂房吹扫稳压器卸压箱、稳压器下泄管线的安全阀和反应堆冷却剂疏水箱;另一部分气体从主气流中分离出用于吹扫容控箱。两部分吹扫气流在吹扫完相应的设备和管线后返回吹扫段。
稳态运行模式是系统的主要运行模式,在该模式下,滞留单元的运行压力为0.5×105Pa(g),基本无气体向环境释放。
1.2 波动运行模式
波动运行模式仅发生在核电厂启动、停运等相对较短的时间。负荷跟踪运行不计入该模式,主要原因是负荷跟踪运行时无过剩水产生,向一回路注入及排出的冷却剂体积平衡,与系统相连的气相空间总体积不变[1]。
当核电厂启动或停运时,大量的冷却剂进入冷却剂贮存箱,这将导致冷却剂贮存箱中的液位升高,容器中气相空间被压缩,过剩的气体将进入废气管理系统,造成系统负压段的压力升高。
另外,核电厂停运阶段打开反应堆压力容器顶盖前,将通过氮气吹扫以除去积聚的放射性惰性气体,这些气体也将进入系统。
为了维持系统吹扫段的压力恒定,需降低循环气体的体积流量,使得进入滞留单元的气体流量增加,系统中的功能监测模块会探测到这部分波动气体,系统自动转换至波动运行模式。
在波动运行模式下,通过提高滞留单元的运行压力来增加其贮存能力以及活性炭的吸附性能。滞留单元增加的贮存容量必须满足高流量时放射性惰性气体自然衰变要求的滞留时间(对于Kr,≥40d;对于Xe,≥40h)。
系统从稳态运行模式切换至波动运行模式后,会以波动运行模式运行40d,从而为惰性气体提供足够的滞留衰变时间。
2 计算方法
2.1 计算周期
EPR 堆型燃料循环周期从12~24 月不等,本文采用12个月燃料循环进行分析,12个月燃料循环模式可覆盖1年内气体运动的所有工况(包括机组正常运行和启停等)。总体来说,换料周期越短,由冷却剂运动引起的气体的运动速度越快;同时气体波动的频率高也将导致气体在系统中的滞留时间缩短。因此,采用12个月作为计算周期是保守的。
2.2 活度浓度计算
为确定最终向环境释放的活度流量,需建立活度浓度计算模型。活度浓度计算由3部分组成:冷却剂活度浓度的确定、系统吹扫单元活度浓度的确定、滞留单元活度浓度的确定。模型示意图如图1所示。
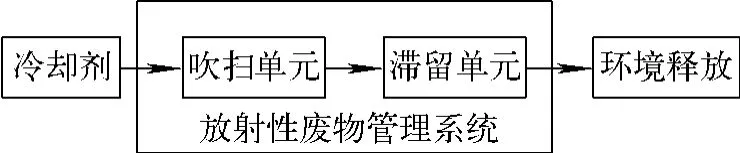
图1 活度浓度计算模型Fig.1 Calculation model of activity concentration
2.3 冷却剂活度浓度
EPR 堆型冷却剂相关源项活度浓度及峰值因子列于表1。
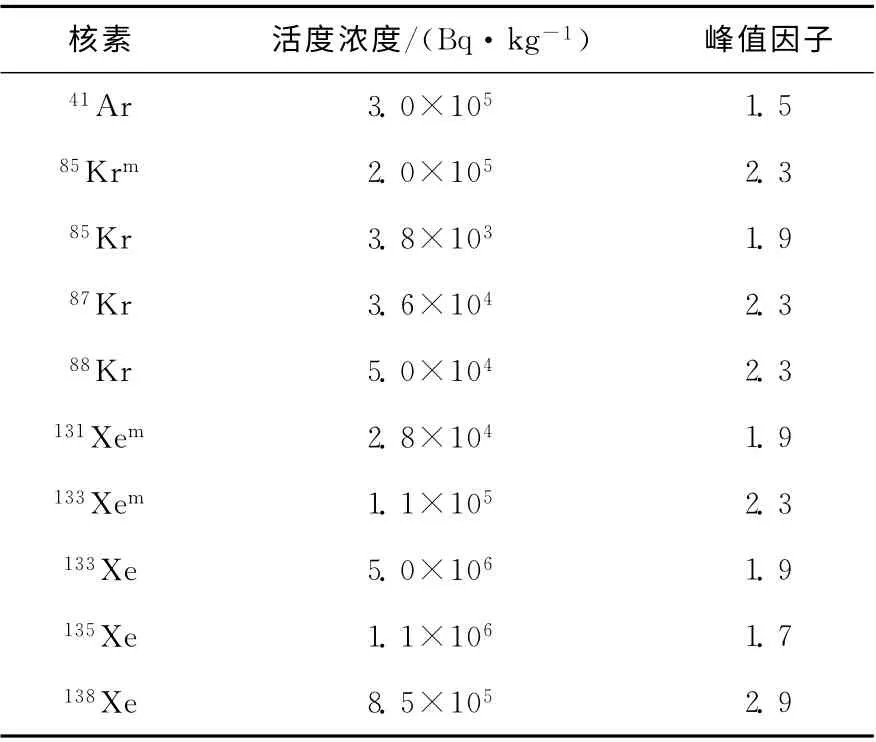
核素 活度浓度/(Bq·kg-1) 峰值因子41 Ar 3.0×105 1.5 85 Kr m 2.0×105 2.3 85 Kr 3.8×103 1.9 87 Kr 3.6×104 2.3 88 Kr 5.0×104 2.3 131 Xem 2.8×104 1.9 133 Xem 1.1×105 2.3 133 Xe 5.0×106 1.9 135 Xe 1.1×106 1.7 138 Xe 8.5×105 2.9
建立模型时假设:停堆前冷却剂活度浓度是恒定的;停堆期间冷却剂活度浓度增加,因此需考虑峰值因子的影响;停堆后活度浓度降低。
2.4 吹扫单元活度
吹扫单元主要用于对容控箱、冷却剂贮存罐、硼酸贮存罐、除气设备和补气设备等主要设备的吹扫。
图2为吹扫单元模型,其他与系统相连部分的放射性气体预期析出量很小,因此这些管线中气体的滞留时间等于气体在主要吹扫管线中的滞留时间。
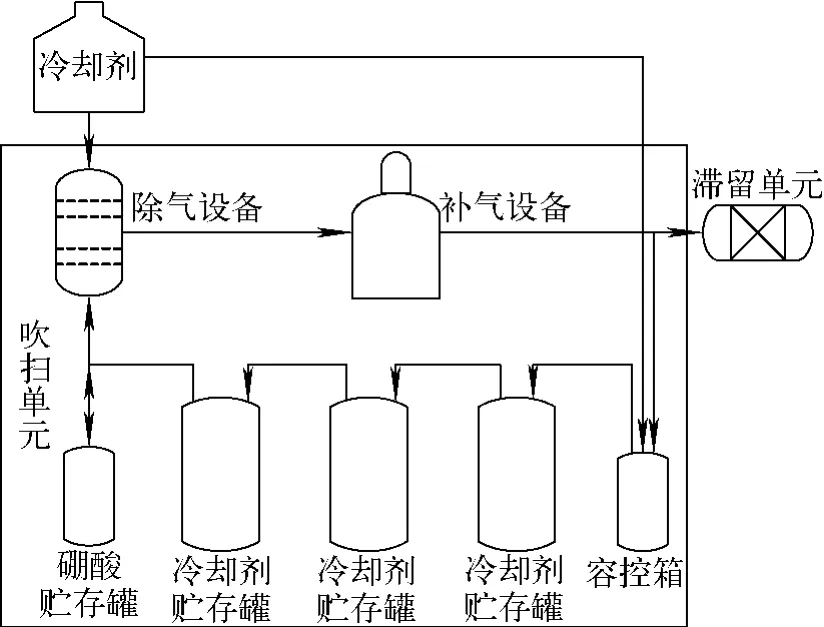
图2 吹扫单元模型Fig.2 Purge unit model
针对模型中不同部分,活度浓度Cn+1,m,r的计算方法如下。
1)管道部分

其中:n为迭代步骤;m 为设备代号;r为核素代号;Cn+1,m,r为第n+1时刻第m 号设备核素r的活度浓度;Cn,m-1,r为第n 时刻m 号前一设备核素r 的活度浓度;λr为核素r 的衰变常量;Δt为时间间隔。
2)除气设备和容控箱
从图2所示模型可看出,在除气设备和容控箱中会引入一部分系统外的冷却剂,活度浓度计算公式如下:
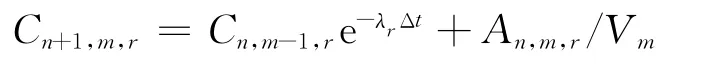
其中:An,m,r为第n 时刻进入到m 号设备核素r的总活度;Vm为m 号设备的气相空间体积。
3)冷却剂贮存箱
冷却剂贮存箱的气相空间体积会发生变化,核素也会在其中发生衰变,活度浓度计算公式如下:

其中,Vin为新引入的气体体积。
4)补气设备
补气所使用的气体不带放射性,因此会稀释系统中原有气体的活度浓度,计算公式如下:

其中:Qm,n为第n 时刻经过m 号设备的系统流量;Qa,n为第n 时刻补 气流量;Ca,n,r为第n 时 刻m 号设备补气中核素r 的活度浓度。
2.5 滞留单元活度
滞留单元与2.4节中的管道部分类似,只是随运行模式不同,延迟滞留的时间存在差异,计算公式如下:
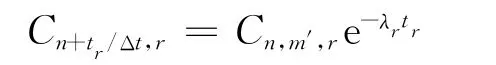
其中:tr为核素r 的滞留时间;m′为滞留单元前的设备代号。
3 系统参数及工况分析
3.1 系统参数
从2.4节给出的吹扫单元活度计算公式可知,计算时需用到一些系统参数,具体如下。
1)系统总参数
所需的系统总参数包括系统和被服务设备的体积、吹扫单元的吹扫气体流量、吹扫单元的气体泄漏率以及吹扫单元压力等。
2)冷却剂参数
放射性惰性气体均来自于冷却剂,因此需要冷却剂相关参数,包括冷却剂水装量以及硼和氚的排放量。
3)除气参数
除气发生在控制棒插入堆芯前72h至一回路降到3/4水位期间,所需参数为除气流量。
4)容控箱参数
容控箱被持续吹扫,保守假定容控箱中的冷却剂被完全除气,所需参数为容控箱的液相体积、气相体积、冷却剂的质量流量、吹扫气体流量以及气相空间压力。
5)冷却剂贮存罐参数
冷却剂贮存罐被连续吹扫,但由于除气过程发生在除气设备或容控箱中,因此不需考虑除气过程,所需参数为容器数量、最大气相空间体积以及最小气相空间体积。
6)硼酸贮存罐参数
硼酸贮存罐不需吹扫,容器内气体将根据液位变化进入或排出废气管理系统。电厂停运时,由于硼酸注入一回路造成容器上方贮存一定量气体;当电厂正常运行时,气体又以缓慢的速率排出。所需参数为容器体积。
7)滞留单元参数
根据相关标准要求,对Kr的同位素滞留时间不少于40h,对Xe的同位素滞留时间不少于960h,而实际电厂运行时滞留单元对Kr和Xe的滞留时间远超过限值要求。
EPR堆型滞留单元采用活性炭对惰性气体进行动态吸附,在动态吸附过程中,裂变产生的惰性气体Kr、Xe相对于载气(氮气)在活性炭上发生物理吸附,而载气不被吸附,这与气相色谱的原理相似。滞留时间可通过下式计算:
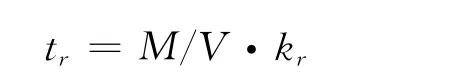
其中:tr为核素r 的滞留时间,h;M 为活性炭质量,g;V 为 运 行 工 况 下 的 气 体 流 量,cm3/h;kr为活性炭对核素r 的动态吸附系数,cm3/g。
3.2 电厂工况分析
气体运动过程,特别是滞留衰变过程与电厂运行工况密切相关,本节分析电厂停堆、启动及功率运行期间影响气体运动的所有工况[2](表2)。
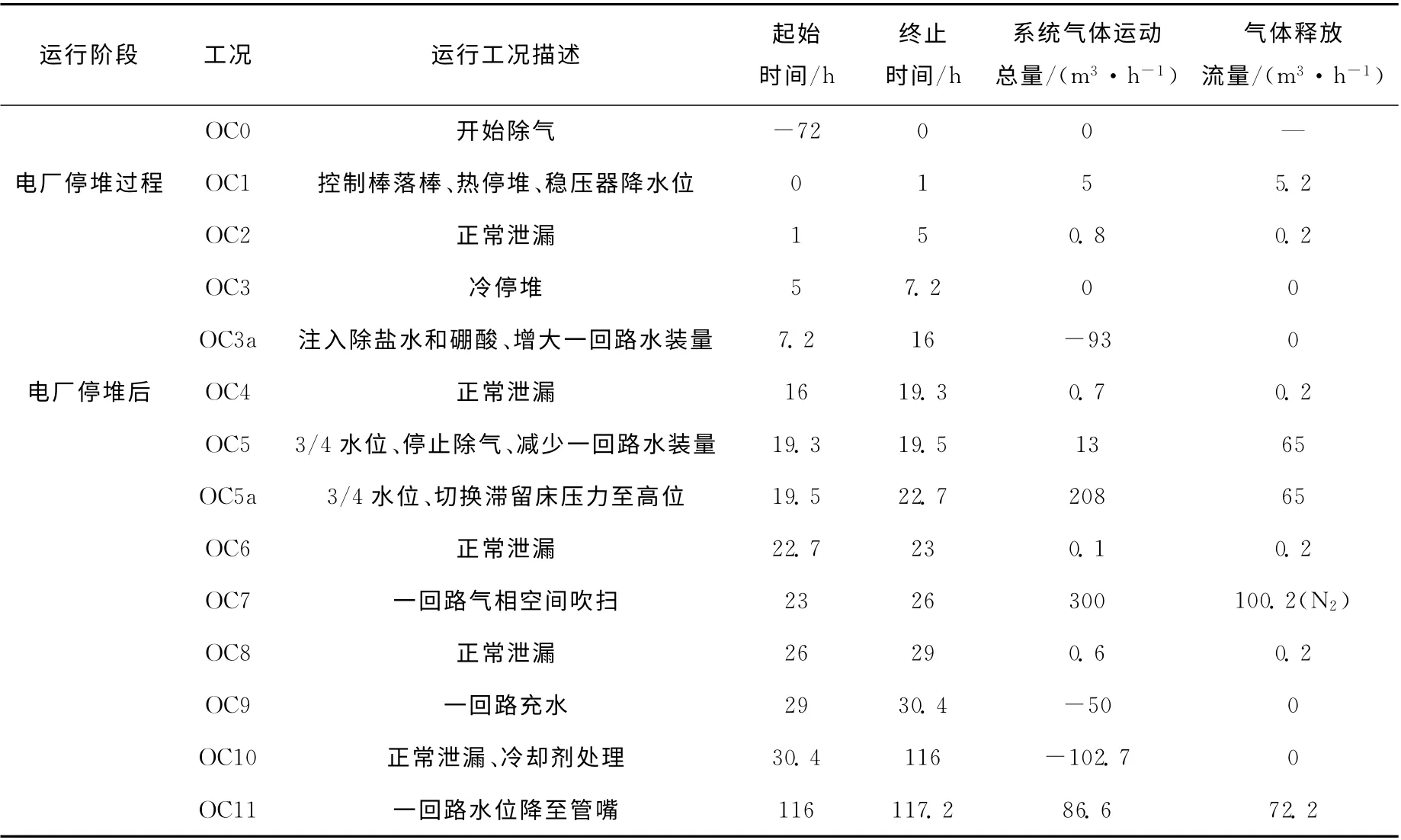
气体释放流量/(m3·h-1)运行阶段 工况 运行工况描述 起始时间/h终止时间/h系统气体运动总量/(m3·h-1)OC0 开始除气 -72 0 0 —电厂停堆过程 OC1 控制棒落棒、热停堆、稳压器降水位 0 1 5 5.2 OC2 正常泄漏 1 5 0.8 0.2 OC3 冷停堆 5 7.2 0 0 OC3a 注入除盐水和硼酸、增大一回路水装量 7.2 16 -93 0电厂停堆后 OC4 正常泄漏 16 19.3 0.7 0.2 OC5 3/4水位、停止除气、减少一回路水装量 19.3 19.5 13 65 OC5a 3/4水位、切换滞留床压力至高位 19.5 22.7 208 65 OC6 正常泄漏 22.7 23 0.1 0.2 OC7 一回路气相空间吹扫 23 26 300 100.2(N2)OC8 正常泄漏 26 29 0.6 0.2 OC9 一回路充水 29 30.4 -50 0 OC10 正常泄漏、冷却剂处理 30.4 116 -102.7 0 OC11 一回路水位降至管嘴116 117.2 86.6 72.2

气体释放流量/(m3·h-1)OC12 正常泄漏 117.2 180 12.6 0.2 OC13 一路回充水至法兰面 180 182.4 -76.5 0 OC14 正常泄漏、冷却剂处理 182.4 398 107.8 0.5 OC15 降水位至3/4液位 398 398.7 45.5 65 OC16 正常泄漏 398.7 409.4 43.1 0.2 OC17 一回路充水至冷停堆液位 409.4 416.2 -220.3 0 OC18 正常泄漏 416.2 420 0.8 0.2电厂起堆过程 OC19 控制棒提升,一回路升温 420 428 83.7 11.6 OC20 正常泄漏 428 455 5.4 0.2 OC21 升至满功率 455 456 -4.5 0功率运行 OC22 正常泄漏 456 477 4.2 0.2 OC23 冷却剂贮存罐补水 477 498.6 162 7.7 OC24 正常泄漏 498.6 502.6 400 100.2 OC25 正常泄漏 502.6 979.4 95.4 0.2 OC26 切换滞留床压力至低位 979.4 992.6 255.3 20 OC27 正常泄漏 992.6 8 688 1 443.1 0.2 OC28 重新回到OC0 8 688 -72 0.5运行阶段 工况 运行工况描述 起始时间/h终止时间/h系统气体运动总量/(m3·h-1)—
4 延迟滞留计算
4.1 理论基础
核素在活性炭滞留床内的延迟滞留是一个动态吸附过程[3],吸附主要靠两类力:一类是范德华力,另一类是静电力,整个过程类似气相色谱柱。
不同运行工况下,气体进入滞留床,放射性Kr和Xe等核素被吸附在活性炭上,一段时间后这些核素将从活性炭上解吸下来,并被下一段活性炭吸附,以此往复经历一段时间后排出滞留床。计算模型如图3所示,其中Puc为消耗的活性炭份额,%;Puc:oc为OC工况消耗的活性炭份额,%。

图3 延迟滞留计算模型Fig.3 Delay calculation model
4.2 滞留时间计算结果
不同工况下的Puc为:

其中:toc为OC工况的持续时间;Voc为OC工况时流经滞留床的最大流量。
活性炭动态吸附过程可等效为如下数学模型:各工况引入的核素将占据一定量的活性炭空间,下一工况引入的核素将压缩上一工况中核素的滞留时间。因此,核素在滞留床中总的衰变时间为活性炭被该核素充满时刻各工况时间的累加值,即:

根据表2中1个换料周期所对应的机组工况,可得到Kr和Xe的滞留过程及滞留时间(图4)。
4.3 释放浓度计算结果
经上述论证,可知放射性气体源项核素的放射性活度浓度以及释放前在系统内的停留时间,通过将表2所列释放流量以及Kr和Xe衰变一定时间后的活度浓度相结合,便可得出释放的“活度流量”,亦可得到总释放量,如图5所示。
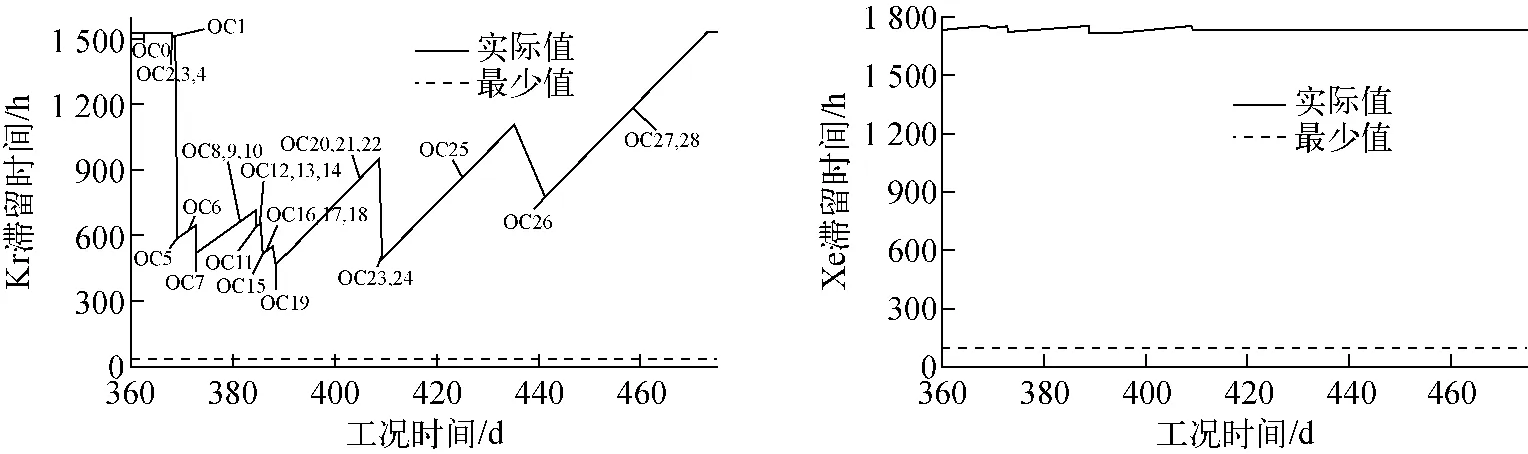
图4 Kr和Xe的滞留时间Fig.4 Decay time for Kr and Xe
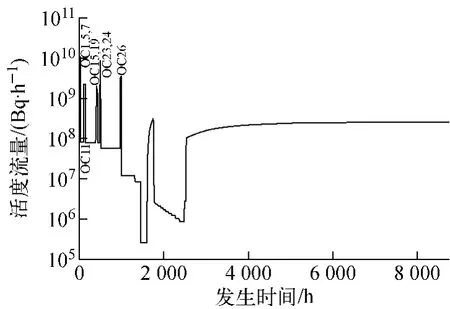
图5 气体释放活度流量Fig.5 Activity flow rate of released gas
需特别注意的是,在所有气体源项中由于85Kr的半衰期很长(达10.76a),系统对其延迟滞留时间可忽略不计。图5所示的活度流量中计入了85Kr的等效活度流量。
5 结论
本文论证了EPR 核电厂放射性气体释放前运动和延迟滞留状态,选取换料周期1年作为计算时长,列举了停堆、除气、吹扫等操作下气体析出的各类工况,并最终推出气体释放活度流量。
通过论证可知,气体释放量峰值发生在工况OC1、OC5、OC7、OC11、OC15、OC19、OC23、OC24 以及OC26。在这些工况下,系统可对Kr和Xe的主要同位素提供足够的延迟滞留时间供其发生衰变,但由于85Kr半衰期很长,系统对其延迟滞留作用可忽略。根据论证结果,本文给出了系统最终向环境释放的活度流量分布趋势。
这一过程为分析EPR 核电厂气态流出物的法规标准符合性奠定了理论基础。
[1] LEIBE D.Gaseous waste processing system TEG SDM,Chapter 2:System operation[R].Germany:SOFINEL,2009.
[2] BROS O.EPR-TSN design transient specification list of loading condition[R].France:AREVA NP,2009.
[3] BECKER P.Sizing report for the delay beds[R].Germany:AREVA GmbH,2013.
