滚动轴承故障信号处理方法与诊断试验研究

徐卫晓，谭继文，温国强

(青岛理工大学，山东青岛266033)

0 前言

滚动轴承是机械设备中最常用的零件，其状态的好坏将直接影响机械系统的工作状态、运行效率和精度。据统计，由滚动轴承引起的机械故障大约占总故障的30%左右［1］，可见，及时地检测滚动轴承的状态信息，并据此诊断其故障，能够大幅度地减少维修成本，杜绝重大损失的发生，从而实现机械设备的正常可靠运行。

滚动轴承在发生故障时，其振动信号表现出现非平稳、非线性的特点，作者首先利用加速度传感器完成了滚动轴承故障状态振动信号的在线采集，然后采用EMD 法将滚动轴承的非平稳信号转换成平稳的IMF 分量，并结合故障信号的时域特征构成时频域特征集，导入到BP 神经网络中进行故障模式识别，从而实现了对滚动轴承故障状态的分类和诊断。

1 经验模态分解理论

经验模态分解(简称EMD)与傅立叶变换、小波包分解等方法相比，因其基函数是由数据本身所分解而得到，且具有直观、直接、后验和自适应等特点，能把复杂的信号分解为有限个固有模态函数(IMF)之和，每一个IMF 分量代表着不同特征尺度的数据系列。由此可见，EMD 分解方法是将非线性、非平稳信号转化成线性、平稳信号的分解过程，具有很高的信噪比。

IMF 分量所包含的频率成分不仅与采样频率有关，而且还随着信号的变化而变化，它必须满足以下两个必要条件:在整个时间段内，该分量的过零点个数和极值点个数要保持相同或最多相差不超过一个;在任意时刻，该分量的上下包络线要关于时间轴对称［2］。

EMD 方法的分解过程也就是数据筛选的过程。原始信号x(t)的分解过程如下［3］:

(1)计算出原始信号x(t)的所有极值点，并用三次样条插值函数逐次拟合极大值和极小值点分别形成上、下包络线，以此涵盖所有的原始信号。

(2)计算出上、下包络线的均值m1，并计算出新的信号序列u1，即

(3)讨论u1是否满足IMF 的条件，如果满足则记为u1=c1，反之则把u1作为原始信号继续重复上述步骤，直到满足IMF 条件为止。则c1即为原始信号的第一个IMF 分量，代表最高频率成分。

(4)通常，需要的是原始信号里的高频成分，则将去掉高频成分的剩余信号记为r1

(5)将r1作为原始数据，重复以上步骤n 次，最终得到c1，c2，…，ck，直到当rn成为一个单调函数不能从中提取到满足IMF 的分量为止。则原始信号x(t)可以表示为:

2 BP 神经网络理论

BP 神经网络全称是反向传播(Back Propagation)神经网络，可以实现输入和输出间的非线性映射。目前BP 神经网络是在故障诊断中应用最广且比较有效的神经网络［4］。

BP 神经网络作为一种前馈网络，具有1 个输入层，1 个输出层和多个隐含层，每层都由多个神经元组成，各个相邻的神经元之间以全连接的方式进行连接，隐藏层传递函数使用S 型函数，输出层传递函数使用线性函数。网络选择以均方误差最小为训练目标，以BP 算法作为网络的学习算法。其中，3 层BP神经网络结构如图1所示。

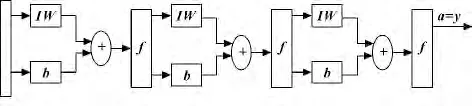
图1 3 层BP 神经网络结构图

3 滚动轴承故障诊断试验研究

3.1 采集振动信号

下面以7202AC 型角接触球轴承为例，将LC0101型加速度传感器分别布置在轴承座的X、Y、Z 3 个方向，对轴承的5 种状态(正常、滚珠磨损、内圈磨损、外圈磨损及保持架磨损)的振动信号进行采集。其中，图2所示为角接触球轴承，图3所示为加速度传感器的布置图。

图2 角接触球轴承

图3 加速度传感器布置图

3.2 时－频域特征提取

由于EMD 分解方法能够将复杂的非平稳的原始信号分解为多个平稳的、线性的IMF 分量之和，因此，采用EMD 分解方法对采集的振动信号进行分解处理［5］，提取分解后的前8 个IMF 分量的能量值作为频域特征;同时提取振动信号的偏斜度、裕度系数、峰度、峭度因子、均方根、绝对平均幅值共6 个时域特征，一共是14 种时－频域特征。如图3所示，由于采集的信号来自X、Y、Z 3 个方向，每个方向有14 种特征，则3 个方向总共42 种特征，将此42 种特征构成特征集作为BP 网络的输入，以备后续处理。图4 为滚动轴承外圈磨损原始信号，图5 为经EMD分解的前10 个IMF 分量。

图4 轴承外圈磨损原始信号

图5 EMD 分解结果

由图5 可知，信号分解到第9 层和第10 层时逐渐变为一个单调函数，对轴承原始信号主要成分影响很小，因此提取包含轴承主要故障信息的前8 个IMF分量的能量值作为频域特征。

3.3 BP 神经网络模型的建立

理论分析表明，一个具有3 层的BP 神经网络能够以任何精度逼近任何连续函数，具有很强的非线性映射能力［6］，因此，选用3 层BP 网络构建网络模型。

由于隐含层神经元个数的多少将影响到网络训练和学习的有效性和准确性［7］，因此，网络设计时主要确定隐含层神经元的个数。其中，输入层节点数:分别提取轴承X、Y、Z 3 个方向的振动信号，每个方向取前8 个IMF 分量能量特征值和6 种时域特征(偏斜度、峰度、峭度系数、裕度、均方根值、绝对平均幅值)共14 个特征值，总共42 个特征值为BP 网络输入，则输入层节点数为42;输出层节点数:即轴承故障的种类数，包括正常轴承、滚珠磨损、内圈磨损、外圈磨损和保持架磨损5 种状态，因此输出层节点数为5。隐含层节点数按以下公式进行确定:

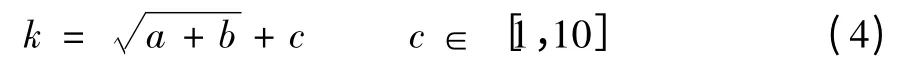
式中:k 为隐含层节点数;a 为输入层节点数;b 为输出层节点数;则代入公式可得7.7≤k≤16.7。经过MATLAB 软件的不断调试，验证当k =16 时能使网络收敛较快且学习步数最少。可见，3 层BP 神经网络的输入层、隐含层以及输出层节点数分别是42、16、5。

此外，由于选取网络的学习速率越小，则系统的稳定性越高，因此，文中选取的学习速率0.1，期望误差0.02，隐含层神经元传递函数为logsig，输出层神经元传递函数为purelin，则有net =newff(minmax(P)，［16，5］，{'logsig'，'purelin'}，'trainrp');进而完成BP 网络模型的建立。

3.4 故障诊断模型的测试与训练

利用3 个加速度传感器分别检测轴承的X、Y、Z 3 个方向的5 种故障状态(正常、滚珠磨损、内圈磨损、外圈磨损和保持架磨损)，并提取每种状态下的振动信号各20 组，其中，16 组作为训练集，剩余4组作为测试集。在MATLAB 环境下，对BP 网络进行训练，得神经网络训练误差变化曲线图，如图6所示。

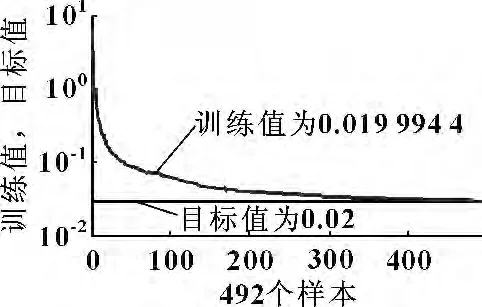
图6 网络训练误差变化曲线

将20 组测试集数据在已训练好的网络内进行测试。限于篇幅原因，训练集的数据不予全部给出，测试集的数据中省略表示X、Y、Z 方向的E2，E2，…，E8和偏斜度、峭度系数、裕度、均方根值等时域特征。其中，E1x，E1y，E1z分别表示X，Y，Z 轴方向的能量值。其中，20 组测试集数据汇总见表1，诊断结果与期望结果的比较情况见表2。

表1 20 组测试集数据

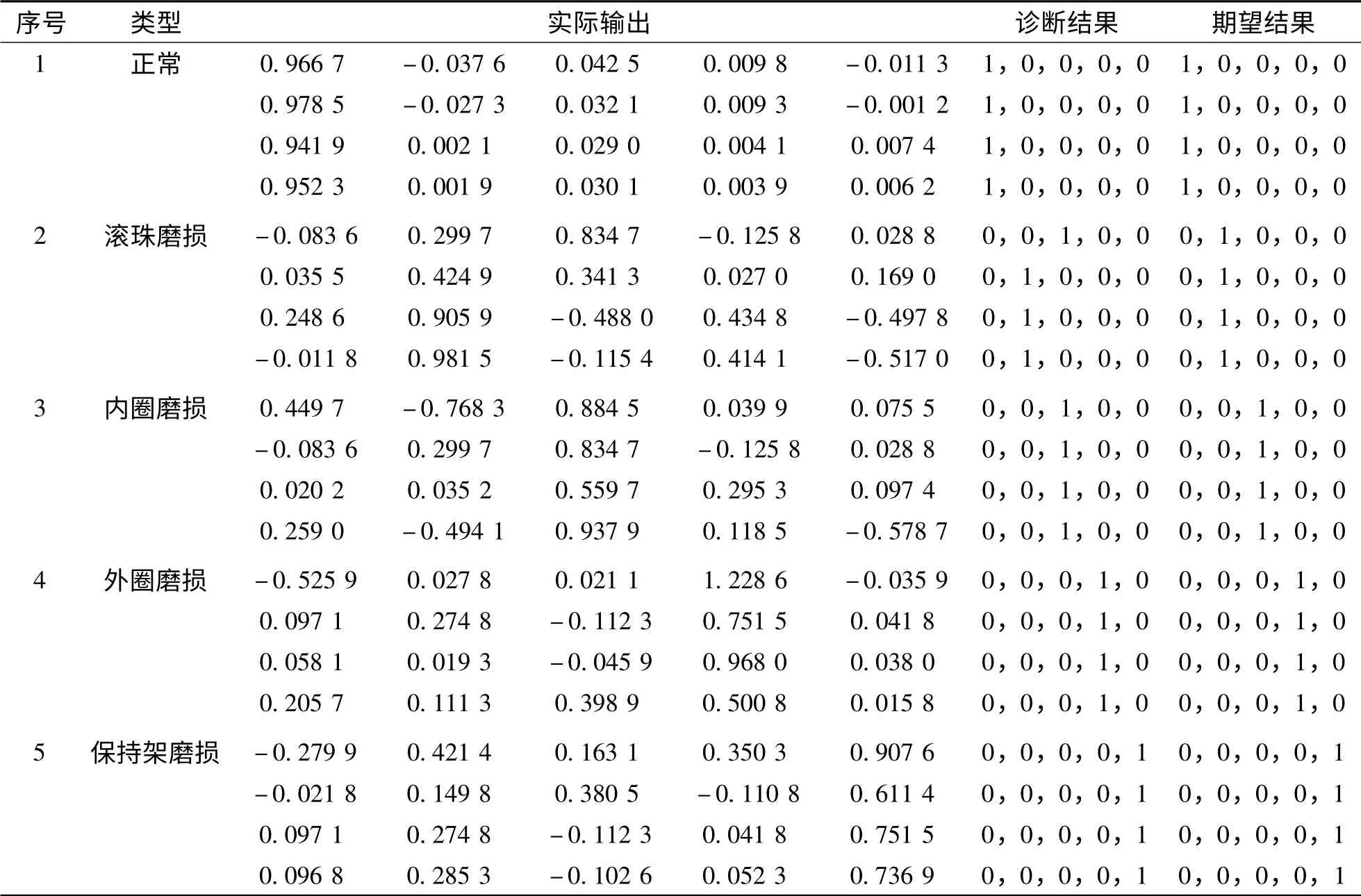
表2 诊断结果与期望结果比较表

从表2 可看出，网络的实际输出结果与期望结果基本一致，只有滚珠磨损一组数据出现诊断错误，因此识别率为μ=19/20 =95%，识别率比较高。可见，经过EMD 分解后的各个分量基本上包含了滚动轴承的主要故障信息，与偏斜度、均方根值等时域特征的结合作为BP 网络的输入特征量，更能准确有效地完成滚动轴承状态的故障诊断。

4 结束语

当滚动轴承发生故障时，其振动信号各个频带的能量都会发生相应的变化，故障振动信号表现出非线性、非平稳特征，且存在噪声干扰，直接进行数据分析很难得到有效的结论。利用EMD 分解方法处理非线性、非平稳信号的优势，结合BP 神经网络的自学习机制，对滚动轴承故障振动信号进行分析处理，证明了EMD 分解后的前几个IMF 分量包含了轴承的主要故障信息，是滚动轴承故障信号处理的有效方法。通过对轴承正常、滚珠磨损、内圈磨损、外圈磨损及保持架磨损等故障进行诊断的结果表明，将EMD 和BP 神经网络相结合建立的轴承故障诊断模型能有效地识别轴承的各种故障状态，且具有良好的通用性和实用价值。

［1］蒋宇，李志雄，唐茗，等.EMD 下轴承故障程度诊断技术的研究［J］.机床与液压，2009(8):257－260.

［2］胡劲松，杨世锡，吴昭同，等，基于EMD 的旋转机械振动信号Winger 分布分析［J］.机床与液压，2003(5):237－239.

［3］周将坤，陆森林.基于EMD 平均能量法的滚动轴承故障诊断［J］.轻工机械，2010，28(2):36－40.

［4］唐贵基，杨玉婧，宋彩萌.基于神经网络的旋转机械振动故障诊断［J］.制造业信息化，2012:40－42.

［5］XU Baojie，RAN liu.Signal Feature Extraction About the Oil Whirl and Oil Oscillation Based on EMD［C］//2nd International Conference on Functional Manufacturing and Mechanical Dynamics.Hangzhou，Zhengjiang，China:Applied Mechanics and Materials，483－487.

［6］刘红光，李丽丽，陆森林.基于BP 神经网络的滚动轴承振动故障诊断［J］.拖拉机与农用运输车，2008，35(6):114－118.

［7］程军圣，于德介，杨宇.基于SVM 和EMD 包络谱的滚动轴承故障诊断方法［J］.系统工程理论与实践，2005，25(9):131－136.