自复位防屈曲支撑钢框架的抗震性能分析

谭燕秋，王朋飞，霍立超，王 帅

(河北工程大学土木工程学院，河北邯郸056038)

自20世纪70年代到现在防屈曲支撑已经历了40余年的发展，现已成为一种技术基本成熟、标准相对完备的抗侧力耗能减震装置。在中震或大震作用下，防屈曲支撑在拉压时均能实现全截面屈服，而不出现支撑构件整体或局部屈曲破坏，从而耗散地震能量，保护主体结构免遭破坏。但是，防屈曲支撑是通过自身发生弹塑性变形来耗散地震能量的，结构在经历大震后势必会产生较大的残余变形。对于即将倒塌或可能经历后续地震的结构，残余变形会对其产生严重影响［1］。孙飞飞等人研究了自复位减震结构的自位复性能［2］。C.Christopoulos、Robert Tremblay［3］等人于2008年研发出自复位防屈曲支撑，并将其运用到钢框架中进行研究。刘璐、吴斌［4］等人对自复位防屈曲支撑做了拟静力试验。研究表明:自复位防屈曲支撑具有复位和耗能的双重特性，可以明显减小结构震后的残余变形。

本文采用通用有限元软件ANSYS对自复位防屈曲支撑刚接钢框架、防屈曲支撑刚接钢框架和钢框架进行罕遇地震作用下的抗震性能对比分析，研究自复位防屈曲支撑在顶点位移、层间位移角、残余变形等地震响应方面的优越性。

1 自复位防屈曲支撑构造原理

1.1 自复位防屈曲支撑的构造

自复位防屈曲支撑的支撑构件为内、外两个方钢管。内管和外管的端部各有一个连接板，用于与结构相连接。如图1所示，左端的连接板穿过左端板的槽孔与内管焊接固定，右端的连接板与外管焊接固定。外管的中段开有槽孔，内管的摩擦板穿过外管的槽孔与外管的摩擦板用高强螺栓相接，在高强螺栓上施加设定的预紧力。四根1 860 MPa级高强度钢绞线锚固在左右端板上，通过端板将预应力传递给内管和外管，也使支撑形成一个整体。在内管和外管之间设置导块，保证支撑的运动方向不发生过大偏移。

1.2 自复位防屈曲支撑的工作原理

当施加在自复位防屈曲支撑两端的外荷载P小于钢绞线的预应力P0与内、外钢管之间的摩擦力F之和时，即0＜P≤P0+F时，内、外钢管之间不发生相对位移，摩擦板不耗能;随着外荷载的增大，当P＞P0+F时，内、外钢管发生相对位移，摩擦板开始耗能;接着外荷载P逐渐减小，当P0－F≤P≤P0+F时(P0≈1.2F)，摩擦板之间的摩擦力反向，不耗能;当P＜P0－F时，内、外钢管发生相对位移，支撑逐渐复位至初始状态，摩擦板耗能。在支撑两端施加拉、压荷载其耗能及复位效果相同。

2 ANSYS计算模型的建立

计算模型为七层五榀两跨的框架－支撑体系，自复位防屈曲支撑自底层至顶层连续布置在第二、第四榀框架中，框架层高3.6 m，跨距7.5 m，模型如图2所示。本结构处于Ⅲ类场地，第二地震分组，抗震设防烈度为8度，罕遇地震下结构阻尼比取 0.05［5］。

2.1 自复位防屈曲支撑滞回模型的建立

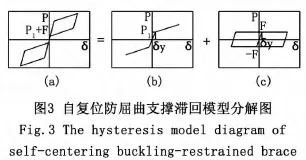
自复位防屈曲支撑的滞回模型为旗形滞回模型，如图3(a)所示，但在ANSYS中没有这种特殊材料的本构模型，因此不能直接建立其滞回模型。本文从自复位防屈曲支撑的力学特性入手，将其滞回模型分解为双折线弹性模型和纯摩擦弹塑性模型两个部分，分别如图3(b)、3(c)所示。分解后的两种模型都可以用ANSYS中现有的材料模型进行模拟，再将这两种单元叠加在一起就得到了自复位防屈曲支撑的滞回模型［6］。对模型(材料特性及相关参数见2.2)施加图4所示的载荷步，得到的滞回曲线如图5所示。

钢框架的梁、柱均采用BEAM188单元模拟，支撑均采用LINK8单元模拟，楼板采用SHELL63单元模拟。

2.2 材料特性及相关参数

钢框架的梁、柱均采用经典双线性随动硬化材料模型，弹性模量E=2.06×105MPa，泊松比0.3，屈服强度205 MPa，强化模量Est=4 120 MPa，密度7 850 kg/m3，柱截面为HW400×400×13×21 mm，梁截面为HN600×300×11×17 mm。

自复位防屈曲支撑由两个LINK8单元叠加模拟，其一为多弹性材料模型，弹性模量E=1.3×106MPa，泊松比0.3，两组应变点和应力点分别是0.000 3 和390 MPa、0.01 和1 950 MPa;其二为双线性随动硬化材料模型，弹性模量E=1.2×106 MPa，泊松比 0.3，屈服强度 360 MPa，强化模量Est=0，密度7 850 kg/m3，两个LINK8单元截面实常数均为 0.001 m2，长度 8.32 m。

防屈曲支撑由一个LINK8单元模拟，为双线性随动硬化材料模型，弹性模量E=2.06×105MPa，泊松比 0.3，屈服强度 345 MPa，强化模量Est=6 589 MPa，密度7 850 kg/m3，单元截面实常数为0.002 2 m2。长度8.32 m。

楼板为各向同性弹性材料模型，弹性模量E=3.0 ×104MPa，泊松比 0.3，板厚 0.15 m，密度 2 500 kg/m3。

2.3 边界条件及地震波的施加

各柱脚结点与地基固接，梁、柱结点为刚接，支撑与梁、柱结点通过自由度耦合的方式进行铰接。

楼面均布活荷载2 kN/m2，重力加速度9.81 m/s2，地震波记录采用1976年宁河天津波地震记录(南北向)，积分步长 0.01 s，持续时间 19.19 s。要得到结构在罕遇地震作用下的地震响应，需将地震波记录峰值调幅为400 cm/s2，调幅后的地震波如图6所示。为得到结构震后的残余变形，在调幅后的地震波记录中添加持时20 s的零值加速度。

3 结果对比

3.1 对比准则的建立

由于自复位防屈曲支撑和防屈曲支撑有共同特征，即它们都具有由第一刚度进入第二刚度的屈服力，故选两种支撑的屈服力(均为750 kN)为对比准则［7］。

地震响应以平行于支撑布置平面的第三榀框架梁、柱结点UX方向的位移为对比准则。

3.2 结构地震响应的对比

三种结构顶点位移响应的对比，如图7所示。

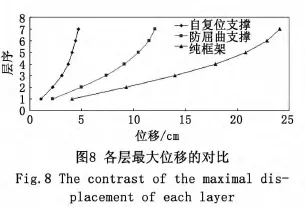
三种结构各层最大位移的对比，如图8所示。

三种结构各层最大层间位移角的对比，如图9所示。

三种结构各层最大残余变形的对比，如图10所示。

4 结论

自复位防屈曲支撑钢框架的顶点最大位移、各层最大位移、层间位移角、残余变形等地震响应方面均明显小于防屈曲支撑钢框架和钢框架。尤其在残余变形方面，自复位防屈曲支撑具有显著的优势，基本上消除了结构震后的残余变形，具有良好的复位效果。

［1］CHRISTOPOULOS C，PAMPANIN S，PRIESTLEY M J N.Performance－based seismic response of frame structures including residual deformations.PartⅠ:single－degree offreedom system［J］.Journal of Earthquake Engineering，2003，7(1):97 －118.

［2］谭燕秋，王颖欣.高层钢结构中BRC跷动技术的减震影响分析［J］.河北工程大学学报:自然科学版，2013，30(1)1－5.

［3］C CHRISTOPOULOS，R TREMBLAY，H J KIM，M LACERTE.Self－centering energy dissipative bracing system for the seismic resistance of structures:development and validation［J］.Journal of Structural Engineering，2008，134(1):96－107.

［4］刘 璐，吴 斌，李 伟，等.一种新型自复位防屈曲支撑的拟静力试验［J］.东南大学学报:自然科学版，2012，42(3):536－541.

［5］GB50011－2010，建筑抗震设计规范［S］.

［6］李黎明.ANSYS有限元分析实用教程［M］.北京:清华大学出版社，2005.

［7］宋子文.自复位耗能支撑结构的地震响应分析［D］.哈尔滨:哈尔滨工业大学，2010.