基于流动数值分析的水轮机蜗壳优化设计研究

石祥钟，董小雪，王利英，岳 莹

(河北工程大学水电学院，河北 邯郸056038)

蜗壳是水轮机的重要组成部件，蜗壳设计是水轮机过流部件设计的重点之一。“等速度距”方法经过长期以来的实践检验，被证明是一种较好的设计方法，但按该理论设计的蜗壳也存在一些问题，如“等速度距”理论假设与实际流动并不相符，椭圆断面部分不符合设计理论(即轴对称有势流动的基本假设)，使蜗壳尾部过流面积较小，周向速度增大，水流运动方向改变增大，而使水头损失较大［1］。本文为了探索蜗壳优化设计方法，设计出最理想的蜗壳，采用目前先进的数值分析方法，应用 CFD 软件详细分析蜗壳内部流动［2－4］，研究蜗壳工作特性，发现传统设计理论的不足，探索改进方法，实例研究表明，将以CAD－CFD技术为基础的优化设计方法用于蜗壳设计，可得到较好结果。

1 理论蜗壳研究

1.1 理论蜗壳内部流动数学分析

蜗壳主要有两个功能:一是使水流形成轴对称向心流动，将水流从四周均匀引入导水机构和转轮;二是使水流形成轴对称环流，其环量值应满足转轮进口环量要求，使水轮机保持高效率工作。如果假定其中流动为有势流动，一个理论蜗壳中的流动可视为涡和汇的叠加。

在极坐标下，涡加汇的流函数为［5］

涡的环量

汇的流量

解式(1)、式(2)、式(3)且当b为常数时得

式中r－极径;θ－极角;Vr－径向速度;Vu－周向速度;b－蜗壳高度;C1、C2－常数。

由此可知，蜗壳外壁轮廓应为等角螺线。

1.2 理论蜗壳设计

以HL160－25为研究对象，为其设计一个外壁轮廓为等角螺线的理论蜗壳。设计水头120 m，单位流量670 l/s，单位转速67 r/min，转轮标称直径25 cm，导叶高度56 mm，座环进口半径21 cm。

根据水轮机中的相关计算公式［6］

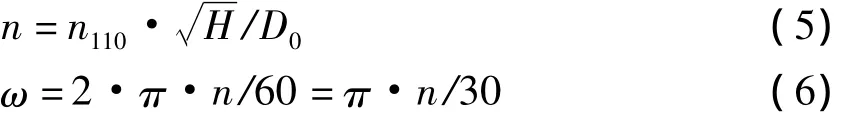
如假定设计工况下转轮出口环量为0，根据水轮机基本方程式得

由式(5)、式(6)、式(7)可得

式中n－转轮的设计计算转速，r/min;H－设计水头，m;D0－转轮标称直径，m;Vul－转轮进口水流绝对速度的圆周分量，m/s;ω－转轮旋转角速度，rad/s;r1－转轮进口边与中间流线交点至水轮机轴线的半径，m。n110－单位转速，r/min。

根据设计工况参数计算得Vul·r1=3.83，故在蜗壳设计时其环量参数k=Vu·r=3.83。对座环进口圆周面上的流动参数进行计算

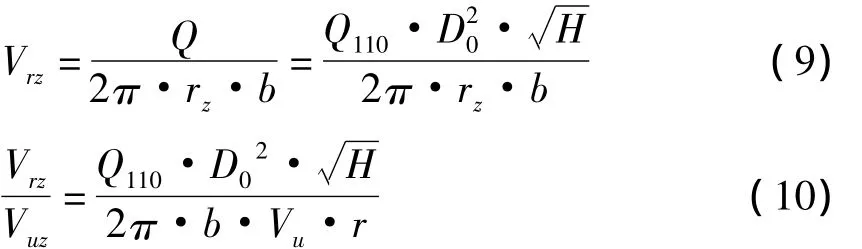
将式(8)代入式(10)即得

式中Vrz－蜗壳出口水流绝对速度的径向分量，m/s;Q－设计流量，m3/s;rz－座环进口半径，m;Vuz－蜗壳出口水流绝对速度的圆周分量，m/s。

代入设计工况参数，设蜗壳所形成的流速与圆周方向的夹角为δ，则

所以，蜗壳外壁轮廓等角螺线方程为

1.3 理论蜗壳内部流动数值模拟分析

如果考虑水是有粘性的，蜗壳中的流动就不能视为有势流动，实际流线与式(13)描述的流线会有一定误差，实际流线用以往经典数学方法无法计算。目前，均采用计算流体力学技术对蜗壳的内部流动进行数值模拟分析［7］。

数值模拟。根据外壁螺线方程确定蜗壳的外轮廓线，高度取导叶高度。为了得到更精确的蜗壳出口参数值，将计算域向后延伸到导叶区域，取计算域出口半径140 mm。采用ICEM软件对其内部计算域进行非结构网格划分，经多方案对比模拟计算，发现网格数量增加到13万以后，继续增加网格数量对计算结果的精度已无影响，最后取网格数量139 119个进行模拟计算。

选用CFX软件，分三种方案进行数值模拟计算。方案一:理想流体，即不考虑水粘性，蜗壳进口速度设定满足“等速度距”条件，方向为螺线在进口处的切线方向;方案二:实际流体，即考虑水粘性，蜗壳进口速度设定满足“等速度距”条件，方向为螺线在进口处的切线方向;方案三:实际流体，蜗壳进口接上足够长的引水管道，考虑引水管道和各种实际因素对蜗壳内流态的影响，设定引水管道进口为法向进流。以上各方案，出口都设为相同的平均压力，分别对蜗壳在设计工况下的内部流动进行数值模拟分析。

模拟计算结果分析。方案一，蜗壳内的水流流态非常理想，流动参数的轴对称性分布很好，水头损失为零，周向速度轴对称性分布最大相对误差为1.84%，径向速度轴对称性分布最大相对误差为2.75%。方案二，流态比较理想，流动参数的轴对称性分布也很好，有非常小的水头损失。方案三，流态不理想，蜗壳进口速度不满足“等速度距”条件，水头损失也略有增加，蜗壳内的周向速度达不到理论设计值，径向速度轴对称性分布也不均匀。为了具体描述蜗壳内流速的分布情况，在半径为170 mm的圆周面上沿周向均匀取8个计算点，将方案二和方案三的周向速度、径向速度列于表1。

表1周向速度和径向速度分布计算表Tab.1 The distributed computing table of peripheral velocity and radial velocity

表2周向速度和径向速度计算表Tab.2 The calculation table of peripheral velocity and radial velocity

对于方案三，分析比较表1中的数据可知，周向速度从蜗壳进口至鼻端呈递增的趋势，但整体均小于理论值，径向速度从进口至鼻端呈递减趋势，但平均值与理论值相同。其原因是当蜗壳进口连接引水管道并考虑了各种实际因素后，蜗壳进口的速度矩在半径方向上不再相等，即实际流动与蜗壳设计的理论假设(有势流动)不相符合，使计算值与理论值差距较大。“方案一”满足理论假设，“方案二”虽然考虑了水的粘性，但设定蜗壳进口满足“等速度距”条件，所以计算结果与理论值也很相近。

1.4 理论蜗壳优化改型

通过方案三的研究可知，按“等速度距”理论设计的蜗壳，其实际流动与预期的理想流动并不相符。为了得到更好的水流流态，流量和流速满足轴对称性分布的要求，需要对螺线型蜗壳进行改型。通过对多种改型方案研究比较，最终发现相对于蜗壳进口，鼻端区域过流断面面积应相应增大。即优化改型措施为:(1)保持进口过流断面面积不变增大鼻端区域的断面面积，可优化蜗壳出口水流的均匀性;(2)保持鼻端区域的过流断面面积不变减小进口面积，可增大蜗壳形成的环量;(3)减小进口过流断面面积的同时增大鼻端区域的面积，既可优化蜗壳出口水流的均匀性又可增大蜗壳形成的环量。本文采用减小进口过流断面面积，并略微扩大鼻端过流断面面积的方法对蜗壳进行改型(方案四)，改型后的蜗壳较改型前流态有较大改善，满足蜗壳设计要求。改型后蜗壳中的水头损失略微增加，不过从工程设计角度来评价是可以接受的。优化改型前后蜗壳外轮廓线对比见图1，改型后蜗壳内水流周向速度和径向速度数据见表2。

2 实际蜗壳优化研究

2.1 原蜗壳内部流动模拟计算分析

按“等速度距”理论［6］，为 HL160－25设计配置一个由圆断面和椭圆断面构成的包角为345°的蜗壳。设计工况和主要结构参数与理论蜗壳相同。采用ICEM软件对蜗壳内部流动计算域进行非结构网格划分，网格数234 235个。选用CFX软件进行数值模拟计算，设定引水管道进口为法向进流(流量457 l/s，流速8.52 m/s)，圆周面出口设为压力出口，湍流模型选用标准k－ε模型。

分析发现从蜗壳进口至鼻端，周向速度呈逐渐增大而径向速度呈逐渐减少趋势，即在鼻端附近周向速度最大、径向速度最小，在蜗壳进口处径向速度最大、周向速度最小。其存在与理论蜗壳方案三相同的问题，因此，应对该蜗壳进行优化改型。

2.2 蜗壳优化改型

对高水头电站由于受经济流速的限制，所取流速系数偏小，导致在蜗壳水力设计时所取的速度矩偏小，因此设计出的蜗壳形成的速度矩比由水轮机基本方程式计算出的偏小。如果设计一个蜗壳使其进口速度矩满足要求，只能减小蜗壳进口断面尺寸(取进口半径108.75 mm)，从而增加进口流速(进口流速11.58 m/s)，这样会使蜗壳的水头损失大大增加(水头损失1.65%)，导致水轮机效率明显降低，这是工程实际中不可接受的。通过不同方案水头损失的比较可知，蜗壳的进口尺寸不应改动(原蜗壳进口半径为125 mm)，对速度矩较小的问题只能靠采用负曲率导叶来增加。对于周向速度和径向速度分布不均匀问题，采取适当加大椭圆断面面积、调整鼻端的位置和鼻端处固定导叶的方向等措施可得到较好解决［8－9］。改型前后蜗壳外轮廓线对比图见图2。

优化改型后的蜗壳水头损失仍然很低，为0.81%，满足工程要求，周向和径向速度的分布均匀性得到很大改善，现取半径为170 mm的圆周面，改型前后周向和径向速度对比见表3。

改型后蜗壳内的压力分布和速度分布也有较大改善见图3。

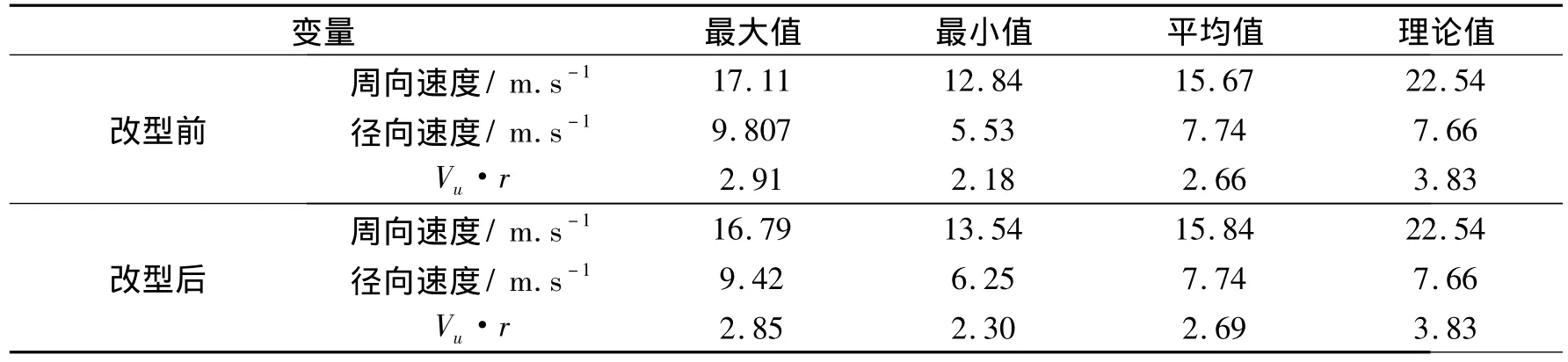
表3改型前后周向速度和径向速度对比表Tab.3 The comparison table of peripheral velocity and radial velocity before and after retrofit

对于中、低水头水轮机，蜗壳进口流速可以取得相对较大(即经济流速系数较大)，使蜗壳形成的速度矩满足水轮机基本方程式的要求，因而，可以通过调节蜗壳进口尺寸来优化蜗壳。

3 结论

理论蜗壳优化改型研究可对实际蜗壳的优化设计指明方向，在利用传统的“等速度矩”法设计的蜗壳的基础上，通过增大鼻端区域的断面面积，

可优化蜗壳出口水流的流动均匀对称性，调整蜗壳进口断面面积可改变蜗壳形成的环量。对于高水头电站，实际蜗壳形成的环量达不到理论设计值，不足的环量应该靠导叶来形成。对于中、低水头水轮机，蜗壳进口流速可以取得相对较大，使蜗壳形成的环量满足基本方程式的要求。

［1］齐学义，晁文雄，郝连松.水轮机全蜗壳圆形断面的水力优化设计方法［J］.兰州理工大学学报，2012，38(6):38－40.

［2］廖伟丽，李建中.混流式水轮机内蜗壳流动的数值研究［J］.大电机技术，2012，6:38－40.

［3］钟晨煜，胡慧婷.基于灰色预测及多目标规划模型的水资源预测及优化配置［J］.四川理工学院学报，2013，26(5):90－95.

［4］WANG FUJUN，LIAO CUILIN，TANG XUELIN.Numerical simulation of pressure fluctuations in a large Francis Runner［J］.Chinese Journal of Mechanical Engineering，2012，6:198－204.

［5］周云龙，郭婷婷.高等流体力学［M］.北京:中国电力出版社，2008.

［6］刘大恺.高等学校教材水轮机第三版［M］.北京:中国水利水电出版社，2011.

［7］ANSYS Company.ANSYS workbench user’s guide［DB/OL］.2009 .http://www.ansys.com.

［8］周文斌.基于混流式水轮机蜗壳改造的型线优化及其数值模拟［D］.兰州:兰州理工大学，2006.

［9］LI YINGWANG，DE HUAWEI.The optimum structural design for spiral case in Hydraulic Turbine［J］.Journal of Elsevier Procedia Engineering，2011，15:4874－4879.