宽厚板坯连铸结晶器铜板的热流密度分布与热分析

吴炳胜，傅彦棉，田倩影，随安海

(1.河北工程大学机电工程学院，河北邯郸056038;2.燕山大学国家冷轧板带装备及工艺工程技术研究中心，河北秦皇岛066004;3.邯郸钢铁集团有限责任公司，河北邯郸056038)

邯钢冷轧机在轧制过程中，机架时常会发生振动，影响其振动的主要原因之一就是轧机的来料。因此，在对冷轧机本身进行研究的同时，也应当要对相应来料的提供者邯钢CSP宽厚板坯连铸机进行研究。连铸机中，结晶器是最核心的设备，而结晶器铜板的热流密度及各项热行为则是结晶器的至关重要的参数，它对连铸坯(冷轧机的来料)的出坯厚度、表面质量、凝固组织均有着直接的影响。在国外，Savage和Pritchard［1］通过实验研究，较粗略地得出了结晶器铜板的热流密度与凝固时间τ的平方根成正比的关系;Park［2］等通过对热传导反算得到了薄板坯结晶器热流密度的分布。在国内，Yao和 Yin等［3－4］对圆柱坯结晶器进行温度实测，同时进行铜板和铸坯间热阻的调整，实现热流密度反算研究;蔡兆镇、朱苗勇［5－6］通过开发坯壳/铜板界面热流模型，并进行热/力耦合模型动态求解铜板热流密度分布。

本文鉴于以上国内外学者对板坯结晶器的各项研究，基于邯钢CSP宽厚板坯连铸机结晶器铜板的有限元模型，并根据铜板上热电偶的实测温度，建立并通过热流密度非线性估算模型，反算获得铜板的热流密度，并且结合生产时的各项数据研究铜板的各项热行为。

1 铜板有限元传热模型

1.1 模型简化假设

不考虑拉速在连铸过程中的变化，铜板的三维传热视为稳态过程［7］;在铜板的高度方向上，视铜板与水槽的交界面的传热系数为定值，水槽入出口之间冷却水温成线性变化，在铜板等高处冷却水温保持相同［8－9］;不考虑铜板向周围环境的散热影响;不考虑铜板的锥度问题，将其视为平直型铜板;将铜板上用于固定的钢制螺栓视为同样形状的铜板，不考虑它对铜板传热的影响;Cu和Ni－Fe的热物性参数各向同性。

1.2 控制守恒方程

将铜板的三维稳态传热视为单向导热，将温度T作为控制变量，传热微分方程有如下表达式:

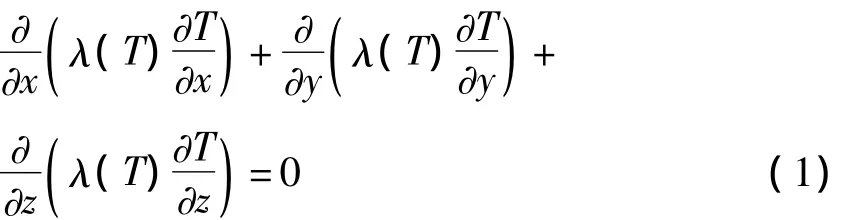
式中x、y、z－铜板的宽度、厚度、高度方向上的坐标/m;λ(T)－导热系数/W·m－1·℃－1;T－温度/℃。

1.3 模型边界条件

铜板热面。根据Savage和Pritchard［1］提出的结晶器热流密度公式，利用拉速可将凝固时间转换为离弯月面的距离，同时处于弯月面以上的热流密度认为是线性分布的。由此，给出铜板热面的热流密度为式中A和B－反算模型的待定系数;z－距弯月面的高度坐标(弯月面中心为坐标原点，正方向为朝下)/m。

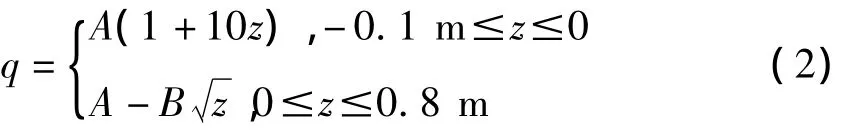
鉴于铸坯角部在实际连铸过程中，会较快的凝固并收缩与铜板之间产生间隙，本文将距角部25 mm的热流密度线性减小至铜板中心处的67%。

铜板冷面。本文将铜板冷面区分为水槽面、与背板接触面，采用不同的边界条件处理用以考虑对铜板温度的影响。

水槽面:冷却水与铜板水槽之间主要为对流传热，并给出对流传热系数hw的计算式如下［10］

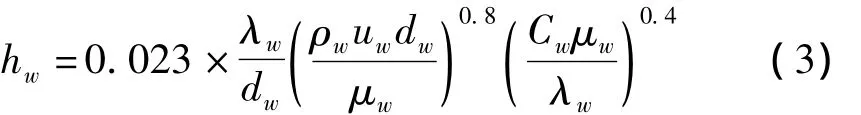
式中dw－水槽的当量直径/m;dw=4A/l，(A－浸湿面积，l－浸湿周长)/m;uw－水的流速/m·s－1;λw－ 水的导热系数/W·m－1·℃－1;μw－ 水的动力粘度/Pa·s;ρw－水的密度/kg·m－3;Cw－水的比热容/J·kg－1·℃－1。

与背板接触面:与背板接触面的温度和周围的空气温度大致一样，故将其设为绝热边界。

根据铜板传热的对称性，铜板对称面设为对称传热边界。

1.4 研究对象及各项物理参数

本文以邯钢CSP宽厚连铸机结晶器铜板为主要研究对象，运用ANSYS有限元分析软件，建立1/4铜板三维有限元模型，如图1所示，宽面、窄面铜板的高度为900 mm，浇铸时所处的弯月面距铜板的上顶面100 mm，铜板内冷面所有冷却水槽的高度均为850 mm，距离铜板的上下顶面都为25 mm。宽面铜板两相邻钢制螺栓之间有五个水槽均匀的分布在其中，为确保螺栓处的有效冷却，靠近螺栓处的水槽为深水槽。窄面铜板中间部分均匀分布着九个水槽，其与宽面铜板接触侧分别布置有一个与窄面铜板内法向成15°夹角的斜水槽。铜板内热面均镀有一层1.5 mm的Ni－Fe层。宽面铜板在位于其上顶面以下200 mm、300 mm和400 mm处分别装有一排热电偶，每排以117 mm间距分布热电偶八个;窄面铜板则只有两个位于其上顶面以下200 mm、300 mm的热电偶，分布位置为铜板斜水槽与深水槽的中心处。热电偶以22 mm的深度插入铜板，如图2所示。

2 热流密度反算模型

本文采用基于最小二乘法的非线性估算法进行反算模型的建立，使热电偶实测温度值和每次迭代之后各测试点的计算温度值之差的平方和达到极小［11－14］。本次测试的宽面铜板有三排热电偶，本文只根据其与窄面铜板一致的距上顶面200 mm、300 mm处的热电偶实测值，建立反算模型，使其实测值与计算值之差的平方和函数F(q)极小，即 ∂F(q)/∂q=0，如下式

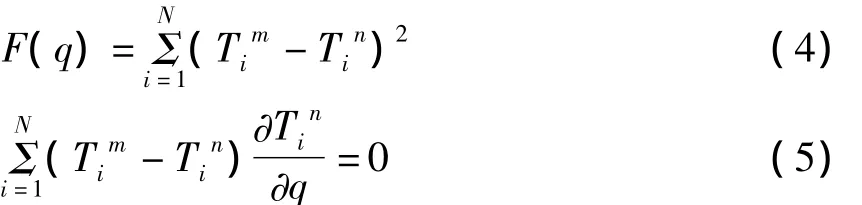
式中i－热电偶的编号;N－热电偶的总数;第i热电偶的实测温度值;Tin－该测试温度的第n

次迭代计算温度值/℃;q－热流密度/MW·m－2。

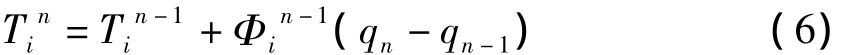
式中qn－第n次迭代的热流密度;－敏感系数。的计算可按显示差分式

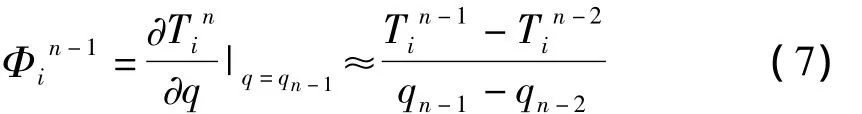
将式(6)和式(7)代入式(5)得

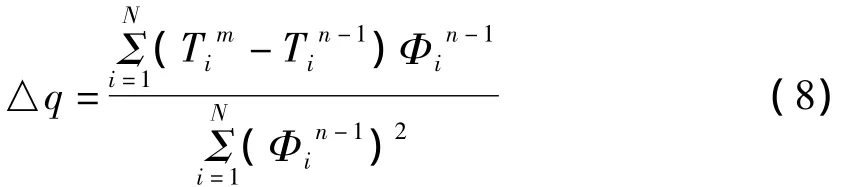
式中 Δq=qn－qn－1，按照式(8)进行热流密度迭代计算，直到Δq/q＜ε为止。

通过本模型，得出了在每次迭代过程中铜板宽面、窄面的上、下放置热电偶处的热流密度q1j与q2j，并联立方程组确定式(2)的系数Aj、Bj，如下式

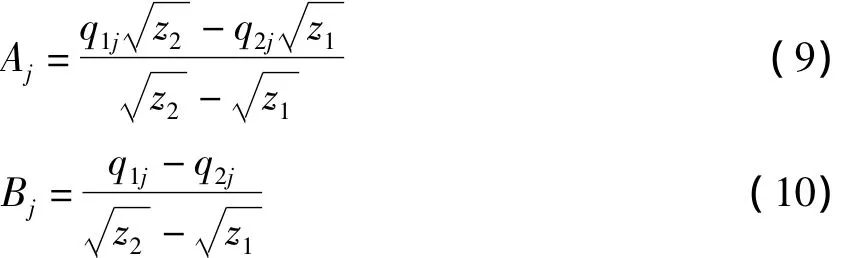
式中j－宽面、窄面;z1=0.1 m，z2=0.2 m。

3 计算结果和分析

在钢液凝固成带有薄壳的铸坯时，绝大部分的热量都由冷却水带走，由此根据热平衡方法来验证非线性估算模型是否有效的设想是可行的。本文通过对各个热电偶的实测温度值进行记录并求其平均值，再由本模型估算出计算平均热流密度，与用热平衡方法计算得到的平均热流密度对比，得出宽、窄面的计算平均热流密度值相比热平衡方法计算得到的平均热流密度值的偏差分别为0.16%、0.27%，两者非常吻合。故本模型用于宽厚板坯铜板热流密度的反算，是有效的。由反算得到的宽、窄面的计算平均热流密度值分别为1.147MW·m－2、1.116MW·m－2，上文中式(2)中的参数A和B分别为宽面2.072、1.541与窄面2.125、1.605。

图3为宽、窄面铜板各热电偶实测温度与计算温度的联合温度曲线图，其中宽面铜板的两条温度曲线中最高温度为热电偶实测温度(平均值为130℃与115℃)，而窄面铜板的热电偶位置在距中心线77.5 mm处，实测温度平均值分别为100℃与88℃。由图可见，模型的计算曲线与实测的温度恰好能吻合，更加印证了模型的有效性。此外亦可见，宽面铜板的温度曲线呈现周期性变化，在每个周期内清楚可见螺栓中心处与深水槽处的冷却强度为最弱与最强，分别达到峰值温度与谷值温度，温差大约为13℃，同时在同一个周期内的两个深水槽之间均匀分布三个浅水槽，其温度成抛物线分布，变化较为稳定、均匀、平缓。而窄面铜板的中心处是一个浅水槽，因此温度曲线在距中心处8 mm处温度会略有升高，达到最高温度分别为123℃与116℃，此后由于分布有三个浅水槽和一个深水槽，温度曲线变化平缓。宽、窄铜板的角部由于气隙的较早形成，热流密度减小较快，温度曲线都显著下降。

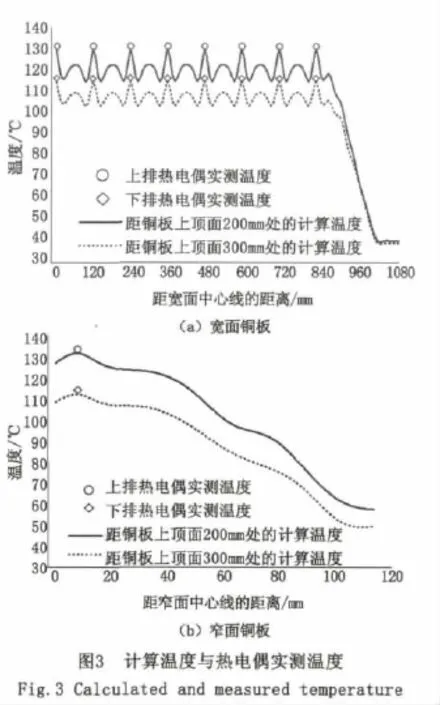
图4为宽面铜板热面的热流密度分布与温度分布图。由图4(a)可见，铜板上顶面到弯月面，热流密度快速增大;弯月面以下区域，热流密度平缓下降;角部位置，由于气隙的较早出现，使得热阻较早增大，热流密度减小明显。由图4(b)可见，弯月面以上区域，铜板热面温度曲线密集;弯月面以下，沿铜板的横向，温度曲线跟随水槽的分布呈波浪状，铜板背面有水槽分布处的热面温度较低;角部位置由于气隙原因，温度下降比较快速。由图4(c)可见，自铜板上顶面至弯月面，热面温度快速升高，从118℃增大为279℃;弯月面之下0～7 mm的区域之内，热流量不大;弯月面之下7～15 mm处，出现温度最高区域，最高温度为291℃，但仍然低于铜板软化再结晶温度(大约为325℃)，不对铜板的正常工作产生影响;最高温度区域并不在铜板的中心区域上，而是在铜板的两侧，且最高温度区域也不是连续的，这与浸入式水口的插入深度及钢液流场在铜板两侧的较为活跃有关;弯月面之下15 mm至距离铜板下底面85 mm的区域内，铜板的温度下降平缓及明显，最低温度为142℃;距离铜板下底面85 mm至铜板底面之间的区域，铜板与水槽没有接触，失去了冷却水的冷却作用，因此温度有所回升，约回升了23℃。

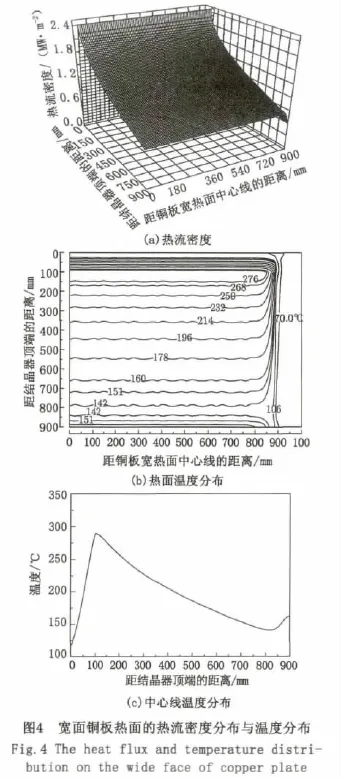
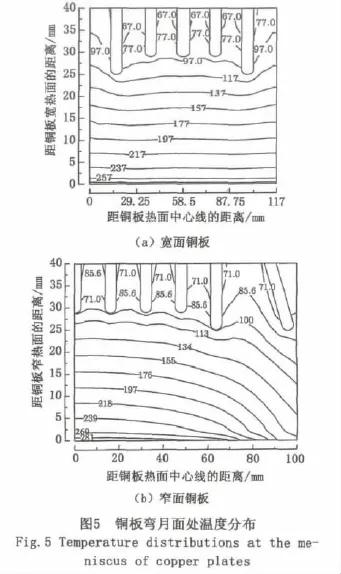
图5为宽、窄面铜板弯月面横截面处温度分布图。由图可知，铜板在该处的温度从热面侧到冷面侧呈下降分布，而温度梯度也逐渐减小;从铜板的宽度方向上看，冷面侧的温度均小于100℃，冷却水在水槽内不会沸腾，同时由于水槽的分布导致冷面侧温度呈波浪状分布，越临近水槽波浪形状越明显;在距铜板热面相同距离处的温度，越临近水槽壁的温度越低，其中螺栓中心线处与水槽壁之间的温差最大，为29.4℃;亦由于铜板热面所镀的Ni－Fe层的导热率比铜板小，在靠近热面处，温差大。由图5(a)可见，相邻两水槽间，波浪状温度曲线沿宽度方向分布均匀，且此种状况保持不变。由图5(b)可见，斜水槽处两侧的温度呈极不对称分布。值得注意的是，铜板的导热性能会随着水垢的增多而减小，故冷却水应使用软水，并定期清洗铜板。

4 结论

1)根据铜板热电偶进行的温度实测，建立并验证了铜板热流密度的非线性估算模型，模型有效。

2)确定了邯钢CSP宽厚板坯连铸机结晶器铜板宽、窄面的热流密度公式。

3)CSP宽厚板坯连铸机结晶器铜板宽面、窄面的计算热流密度分别为1.147 MW·m－2、1.116 MW·m－2;铜板螺栓中心线与深水槽中心线的温差最大，其中宽面铜板处的温差为13℃左右;铜板热流密度与温度均在弯月面处达到最大值，并随着距弯月面的距离的增大而减小，但在距铜板下底面85 mm区域，温度会有23℃左右的回升;在距铜板热面相同距离处，螺栓中心线处比水槽壁处高29.4℃;铜板冷面侧温度均小于100℃，冷却水不会沸腾;斜水槽处两侧的温度呈极不对称分布。

［1］SAVAGE J，PRITCHARD W H.The problem of rupture of the billet in the continuous casting of steel［J］.J Iron Steel Inst，1954(178):269 －278.

［2］PARK J K，SAMARASEKERA I V，Thomas B G，et al.Analysis of thermal and mechanical behavior of copper mold during thin slab casting［C］//83rd Steelmaking Conference proceedings:Pittsburgh，2000:9－16.

［3］YAO M，YIN H B，FANG D C.Real－time analysis on nonuniform heat transfer and solidification in mould of continuous casting round billets［J］.ISIJ Int，2004，44(10):1696－1701.

［4］YIN H B，YAO M，FANG D C.3 － D inverse problem continuous model for thermal behavior of mould process based on the temperature measurement in plant trial［J］.ISIJ Int，2006，46(4):539 －545.

［5］曹兆镇，朱苗勇.板坯连铸结晶器内钢凝固过程热行为研究:Ⅰ.数学模型［J］.金属学报，2011，47(6):671－676.

［6］曹兆镇，朱苗勇.板坯连铸结晶器内钢凝固过程热行为研究:Ⅱ.模型验证与结果分析［J］.金属学报，2011，47(6):678－683.

［7］杨刚，李玉宽，于 洋，等.薄板坯连铸结晶器铜板的三维传热分析［J］.金属学报，2007，43(3):332－336.

［8］LU X D，ZHU M Y.Finite element analysis of thermal and mechanical behavior in a slab continuous casting mold［J］.ISIJ Int，2006，46(11):1652 －1658.

［9］MENG X N，ZHU M Y.Thermal behavior of hot copper plates for slab continuous casting mold with high casting speed［J］.ISIJ Int，2009，49(9):1365 －1370.

［10］张炯明，张立，王新华，等.板坯连铸结晶器热流量的研究［J］.金属学报，2003，39(12):1285－1290.

［11］BECK J V.Nonlinear estimation applied to the nonlinear inverse heat conduction problem［J］.Int J Heat Mass Transfer，1970，14(4):703 －708.

［12］郝守卫，柳百成，张卓其，等.凝固过程中传导热的反问题［J］.清华大学学报:自然科学版，1989，29(2):36－41.

［13］刘元林，唐庆菊，陈焕林，等.脉冲热源激励金属板材缺陷的红外热波检测［J］.黑龙江科技学院学报，2012，22(5):489 －492.

［14］郭志鹏，熊守美，曺尚炫，等.热传导反算模型的建立及其在求解界面热流过程中的应用［J］.金属学报，2007，43(6):607－612.