超高压输电塔在覆冰断线作用下的动力响应

刘锐鹏,颜天佑,张耿斌,许志华,徐辉

(1.广州电力设计院,广州 510075;2.广州供电局有限公司输电管理所,广州 510620)

超高压输电塔在覆冰断线作用下的动力响应

刘锐鹏1,颜天佑1,张耿斌2,许志华1,徐辉1

(1.广州电力设计院,广州 510075;2.广州供电局有限公司输电管理所,广州 510620)

以某500 kV典型输电线路的塔-线体系为模型,借助非线性有限元软件ANSYS/LS-DYNA,在不考虑导线与地面碰撞接触的情况下,模拟不均匀覆冰工况下,四分裂子导线同时断裂、相继断裂两种工况下,断线冲击荷载对输电塔的动力效应。分析结果显示,塔头上的应力和位移动力效应明显,采用拟静力法计算断线冲击荷载是偏于不安全的。

输电线路;不均匀覆冰;四分裂导线;冲击荷载

1 前言

架空输电线路断线产生的纵向不平衡张力是输电塔的重要设计荷载[1],虽然线路断线事故是小概率事件,但一旦发生,不仅会损坏杆塔、绝缘子等电力设施,还会引起局部范围的电力系统振荡,严重时会导致输电杆塔连续倒塔,严重的冰雪灾害造成了多条输电线路的大规模倒塔断线事故,给电力系统造成了严重破坏[2]。

我国学者夏正春[3]利用ANSYS/LS-DYNA数值模拟了输电塔在导地线断线作用下的动态响应,但建立的塔-弹簧模型没有充分考虑塔-线耦合作用;鲍立华[4]用ABAQUS建立了某大跨越输电塔线体系模型,分析了四分裂导线断一根子导线直至断四根子导线工况下断线荷载对输电塔的冲击作用,但其设定的子导线断线工况较理想化;谭庆等[5]以晋东南-南阳-荆门1 000 kV输电线路汉江大跨越工程为参考,利用两塔三线模型分析了断线工况下大跨越输电塔的动力响应,但未考虑子导线的断线工况。国外学者John D.Mozer等[6]对输电线路塔-线体系模型进行试验和数值模拟分析,得到了在断线情况下输电塔顺线路方向的静态、动态响应;M.B.Thomas等[7]提出了基于不同型号参数的输电线断线的时间历程计算方法。

以500 kV典型输电塔-线体系为参考,采用非线性有限元软件ANSYS/LS-DYNA建立两塔三线有限元模型,模拟并分析了超高压输电线路在不均匀覆冰下,四分裂子导线同时断裂、子导线相继断裂工况下输电塔的动力响应,并与拟静力法结果进行对比。

2 基本理论

2.1 基本假设

在建立输电塔-线耦合体系有限元模型和输电线断线分析过程中,作以下假设：

1)忽略输电塔上覆冰对分析结果的影响;

2)忽略导线间隔棒的作用;

3)塔脚处为固结状态;

4)无风工况;

5)边相导线发生断线,断线点靠近导线耐张线夹出口处 (如图1);

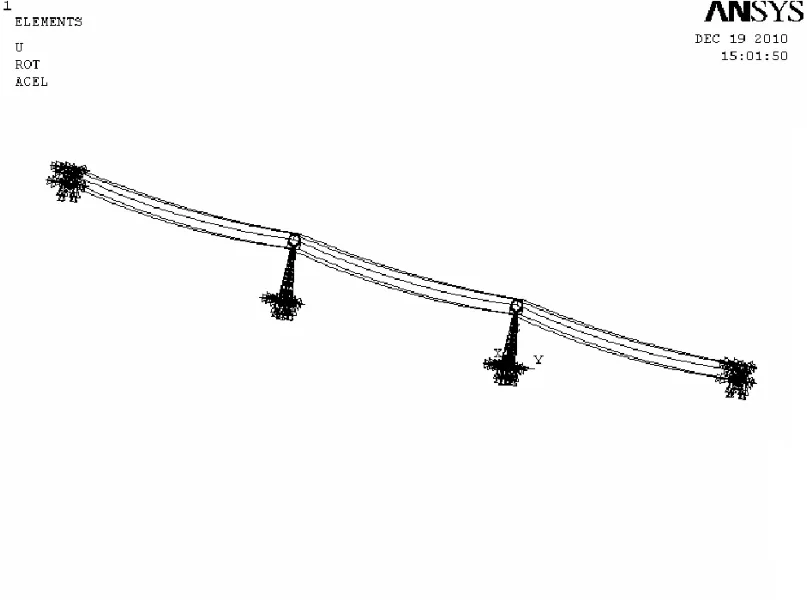
图1 输电塔-线耦合体系的有限元模型

6)认为在极短时间内断线过程即完成,断裂后作用在该导线上的应力在瞬时突变为0,不考虑导线与大地的碰撞接触及脱冰影响。

2.2 体系的动力响应 [z,x]

导地线找形分析是断线仿真的基础,应采用非线性有限元迭代的方法实现。根据导地线的受力和变形特点,采用两节点直线索单元模拟导地线。通过迭代计算,确定各节点在自重和初应力作用下达到力平衡的节点位移向量 {d},即有：

[K({d}]{d}={W} (1)

式中：[K({d})]]为结构刚度矩阵,由于几何非线性,刚度矩阵与空间位置 {d}有关; {W}为张拉力和自重等效节点荷载向量; {d}为节点位移向量。

断线时,由于突然释放了导线的张力,带动断线点导线振动,并沿导线迅速向远处传播,体系在冲击力作用下开始做强迫振动,由于冲击时间很短,体系在获得初始速度后做非线性自由振动,此时体系振动方程为

[M]{d¨(t)}+[C]{d·(t)}+[K({d·(t)})]{d}=0 (2)

式中,[M]为质量矩阵,[C]为阻尼矩阵, [K({d})]]为结构刚度矩阵,{d(t)}为结构的位移响应。

因阻尼的耗能作用,体系最终处在静力平衡位置。

3 有限元模型

某500 kV输电线路,水平档距500 m,架空线两端无高差,直线塔采用5A-ZM4型猫头塔,塔高71.6 m,导线、地线材料特性参数见表1。覆冰厚度取15 mm,覆冰密度取0.8 g/cm3。

表1 导/地线材料特性参数

采用ANSYS/LS-DYNA有限元分析软件建立输电塔-线耦合体系有限元模型,如图1所示。

均匀覆冰厚度取15 mm,不均匀覆冰时将整档架空线按覆冰厚度分为5个区段,每区段水平投影长度100 m,假设同一区段内导线和地线覆冰情况相同。不均匀覆冰分布工况见表2。

表2 不均匀覆冰分布工况

提取导线应力分析可知,线路均匀覆冰时,导线最大应力未超过其最大使用应力;不均匀覆冰工况B和C时,导线最大应力均超过了其最大使用应力,且以工况C时最为严重,故以工况C做为断线时的线路覆冰工况。

4 断线分析

4.1 导线断线仿真

断线模拟主要通过以下三个步骤来实现：

1)分析输电塔-线体系在自重作用下的应力平衡,计算时间为0～5 s;

2)因雷击、闪络、金具磨损等外界因素作用下导线局部应力下降,在严重覆冰后,导线在第5 s突然断裂,模拟四分裂导线同时断裂工况下输电塔-线体系的动力响应,总计算时间为13 s;

3)模拟分析四分裂导线相继断裂情况下的输电塔-线体系动力响应,四分裂子导线相继断裂的时刻分别为计算时间的第5.00 s、第5.10 s、第5.16 s和第5.20 s。

4.2 输电塔的动力响应

选取塔头上代表杆件和节点为研究对象,如图2所示,分析其在两种断线工况下的动力响应。

图2 代表杆件和节点位置

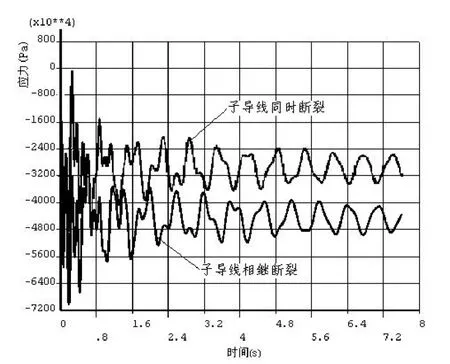
图3 1 611号杆件应力-时间变化

图4 1 799号杆件应力-时间变化

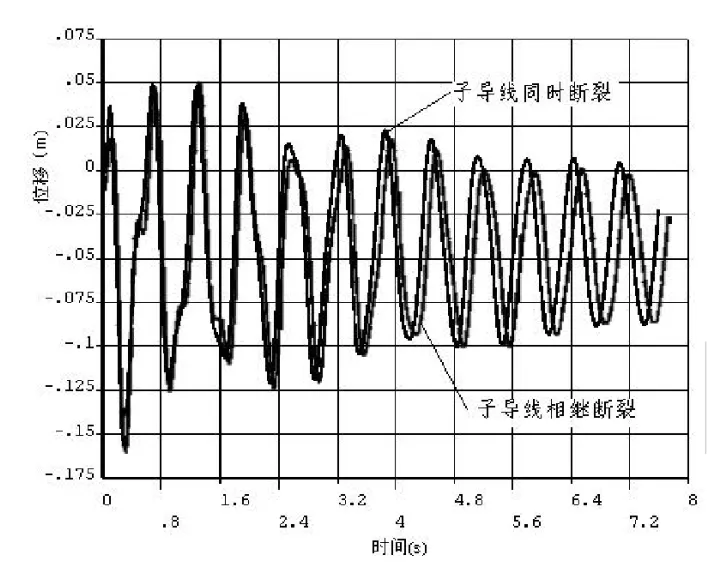
图5 472号节点X方向 (顺线路方向)位移-时间变化

图6 474号节点X方向 (顺线路方向)位移-时间变化

4.3 规范中断线计算方法

按照 《110 kV～750 kV架空输电线路设计规范》中的断线张力工况,采用拟静力法计算断线不平衡张力对塔的静力响应。均匀覆冰厚度取15 mm,输电塔在覆冰断一相导线工况下的荷载如图7所示：

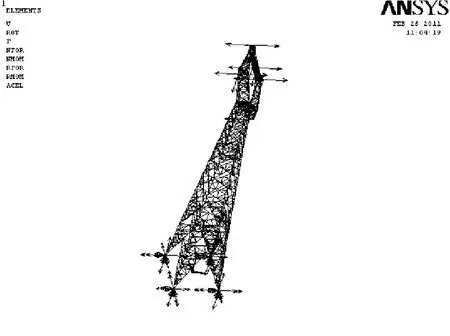
图7 输电塔在覆冰断导线工况下的荷载

4.4 冲击荷载和冲击系数

为评价导线覆冰断线对输电塔的动力响应,引入冲击比η：

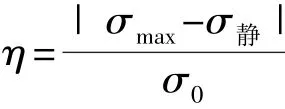
式中,σmax为导线断线后杆件应力的最大值, σ静为利用规范拟静力法计算出的断线后杆件应力值,σ0为正常运行时杆件的应力值。

分别提取断线后输电塔-线体系中的主材杆件 (Z1-Z5)、斜材 (X1-X5)、塔头处塔材 (T1 -T3)进行分析,具体数据见表3(表中拉力为正,压力为负),各杆件具体位置见图8所示。

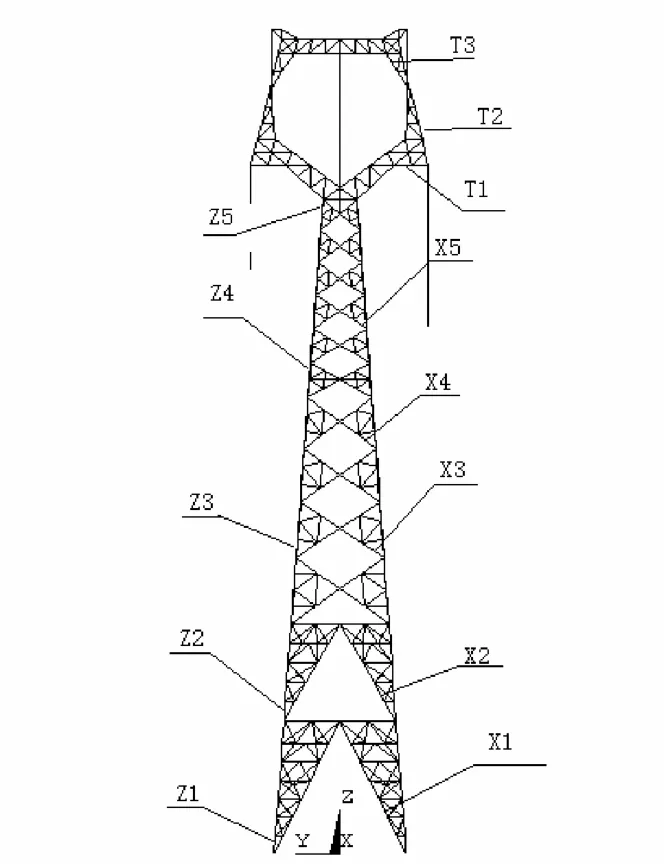
图8 主要分析塔材位置

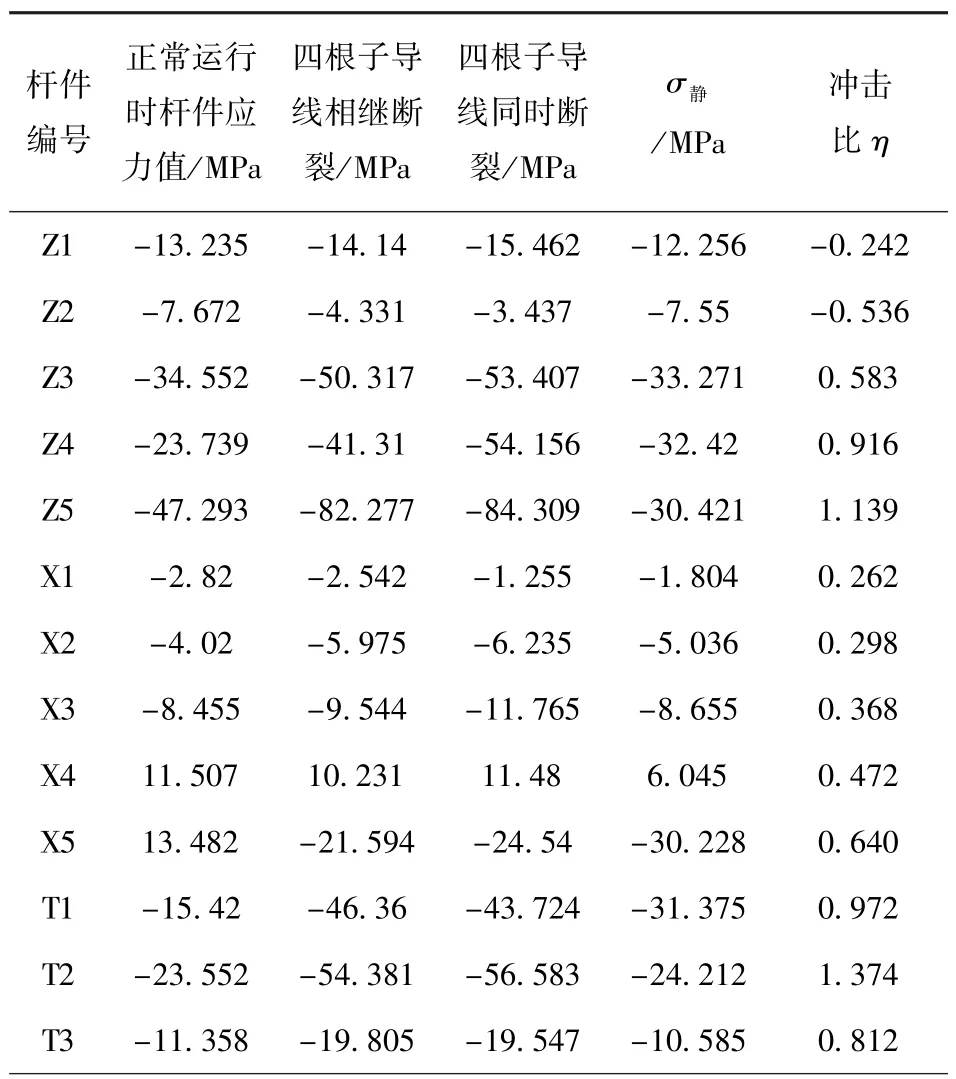
表3 冲击荷载和冲击比

5 结束语

1)由于未断子导线间的相互作用以及其他相导线间动力作用对铁塔的叠加,两种工况下同一杆件随时间变化的受力状态明显不同,杆件拉、压应力状态变化剧烈。

2)浊正值越大,σmax与σ静的差值越大,说明目前线路设计规范中采用拟静力法计算线路断线张力是偏于不安全的。

3)从表3中可以看出,塔头和塔颈处杆件受到冲击作用最大,塔腿处主材受到的冲击荷载最小,塔身中部杆件同样有较大冲击荷载,不可忽视。

[1] 陈景彦,白俊峰.输电线路运行维护理论与技术 [M].北京：中国电力出版社,2009：88-90.

[2] 彭向阳,周华敏,潘春平.2008年广东电网输电线路冰灾受损情况及关键影响因素分析 [J].电网技术,2009,33 (9)：108-111.

[3] 夏正春,梁政平,李黎.大跨越输电塔线的断线振动及控制 [J].武汉理工大学学报,2008,30(9)：84-88.

[4] 鲍立华.输电塔线体系的断线分析 [D].杭州：浙江大学,2008,31-45.

[5] 谭庆,程华,王仲刚.输电塔-线体系在断线作用下的动力响应 [J].后勤工程学院学报,2009,25(3)：14-18.

[6] MozerJ.D.,Wood William A.,Hribar John A.Broken wire tests on a model transmission Line system[J].IEEE transactions on power apparatus and systems,1981,100(3)：224 -228.

[7] Thomas.M.B.Dynamic response of ruptured conductors in transmission lines[J].IEEE Transactions on Power Apparatus and Systems,1982,PAS-101：145-149.

Research on the Dynamic Response of EHV Transmission Tower under Ruptured Icing Conduction

LIU Ruipeng1,YAN Tianyou1,ZHANG Gengbin2,XU Zhihua1,XU hui1
(1.Guangzhou Electric Power Design Institute,Guangzhou 510075; 2.Power Transmission Management Office of Guangzhou Power Supply Bureau Corporation,Guangzhou,510620)

Taking a typical 500 kV transmission tower-line system as an model,using nonlinear finite element software ANSYS/ LS-DYNA,without considering the collision impact between the wire and the ground,simulates two breakage conductions of breaking four sub-conductors at the same time and breaking sequentially under the uneven icing conduction,the dynamic effect of the conductor breakage impact load on the transmission tower is analyzed.The dynamic effects of stress and displacement of the tower head is obvious.

Transmission line;Uneven icing;Four sub-conductors;Impact load

TM75

B

1006-7345(2014)01-0059-04

2013-07-20

刘锐鹏 (1982),男,硕士,工程师,广州电力设计院,从事架空输电线路设计、运行与维护方面研究工作 (e-mail) 30052535@qq.com。