基于交通流参数相关的阻塞流短时预测卡尔曼滤波算法

董春娇 邵春福 周雪梅 孟 梦 诸葛承祥

(1田纳西大学交通研究中心，田纳西37996，美国)

(2北京交通大学城市交通复杂系统理论与技术教育部重点实验室，北京100044)

(3同济大学教育部道路与交通工程重点实验室，上海210804)

为了缓解交通拥挤，各国研究学者提出了多种基于交通流短时预测的诱导、控制策略.作为诱导、控制策略研究的基础，交通流短时预测方法研究具有重要的理论及现实意义.从20世纪60年代开始，人们就把其他领域应用成熟的预测模型用于短时交通流预测，如自回归滑动平均模型(ARMA)、历史平均模型(HA)和Box-Cox法等.随着该领域研究的逐渐深入，又出现了一批更复杂、精度更高的预测方法.从表现形式上可分为基于确定的数学模型方法和无模型算法两大类.前者包括多元回归模型[1]、ARIMA 模型[2]、Kalman 滤波模型[3]、贝叶斯模型[4]及由这些模型构成的各种组合预测模型等;后者则包括非参数回归[5-6]、基于混沌理论的方法[7]、基于突变理论的方法[8]、基于小波分解与重构的方法[9]、支持向量机模型[10]，以及多种与神经网络相关的复合预测模型等[11].基于数学解析模型的方法由于模型本身的局限性，难以处理随机干扰因素对交通流的影响，因而无法反映交通流系统本身的高度不确定性与非线性，预测精度不高;基于知识的智能模型预测方法，通过方法本身的结构机制来获取预测的“经验”、“知识”，以预测下一时段的流量，具有一定的自适应能力，但没有结合交通流参数的特性予以考虑和处理，影响了其预测效果.近几年，一些研究者提出基于交通模拟的交通流预测方法，利用动态交通流分配的预测方法和利用元胞自动机的预测方法等[12].基于交通模拟的预测方法把车辆当作实体，用相关模型与算法描述道路网交通基础设施和驾驶人的交通行为，结合交通流模型，利用计算机微观仿真技术，模拟车辆的动态交通运行状态，从而预测出交通流相关信息.这种方法直观性强，但是由于设定某种规则对交通主体进行描述，往往忽略了交通主体的随机性及离散性特点，实际应用时具有局限性.

目前交通流短时预测建模主体仍停留在针对单点、单断面的交通流参数，很少有针对网络层面城市道路网系统的研究.网络条件下，交通流变化更为复杂，时间及空间的扩展交叉，致使交通流状态不确定性更强.其中，阻塞流作为诱发交通拥挤的根源，其状态下的交通流短时预测研究对缓解交通拥挤具有重要意义.阻塞流状态下，交通流密度较大，速度受前车制约性强，车辆行驶自由度小，车速稳定性差，显示出较大的波动性，当交通流率继续增加，车流会出现走走停停现象.本文以阻塞流状态下交通流时空特性为切入点，通过判断阻塞流状态下交通流率和占有率之间的关系，在分析时间和空间特性的基础上，考虑进出口匝道等影响因素，从交通流守恒方程组出发，借鉴偏微分方程求解Lax-Wendroff格式离散的思想，建立阻塞流状态下交通流短时预测状态空间模型，并设计了基于卡尔曼滤波方法的模型求解算法.最后以北京市某一区域路网为例，进行了实证性研究.

1 阻塞流状态下交通流短时预测状态空间模型

经典的交通流基本图理论[13]和最新的三相交通流理论[14]中，都存在着高密度、低速度的交通流状态.在三相交通流理论中，将这种状态称为阻塞流相，这里的相定义为某种时空状态.本文根据交通流图上参数的分布特征及其在快速路上表征的运行状态，将其称为阻塞流状态.

阻塞流状态下交通流率-密度散点图如图1所示，图中，K为密度;q为断面交通流率;qmax为最大通行能力;qout为阻塞后流出流量;qth为最小通行能力;Kmax为最大密度.此时交通流速度很低，各车道速度趋于一致，交通流率产生较大幅度的下降，这也说明该速度下的交通流出现了或长或短的停顿现象.阻塞流状态下，虽然交通流率大幅度下降，占有率急剧增加，但是交通流率和占有率之间仍存在明显的函数关系.

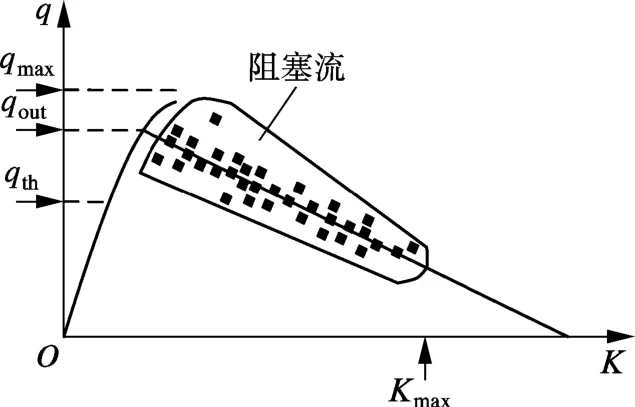
图1 阻塞流状态下交通流率-密度散点图

1.1 无进出口匝道影响的交通流短时预测模型

阻塞流状态下，交通流率和占有率之间具有明显的函数关系，满足交通流守恒方程[13]，即

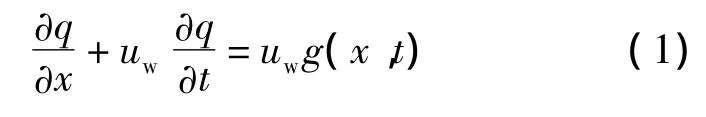
式中，x为断面间距;t为时间间隔;uw为交通波波速;g(x，t)为车辆的产生(或离去)率，即每单位长度、每单位时间内车辆的产生或离去数.

为求解式(1)，针对阻塞流状态下无进出口匝道影响的城市快速路交通流特性，提出如下假设:

1)空间上预测断面的交通流率不仅受相邻上游断面交通流率的影响，而且受相邻下游断面交通流率的影响.

2)t到t+1时段交通波波速为常数，即uw=a.

3)g(x，t)=0.

根据假设条件1)，对求解区域给出网格剖分，构建时空离散节点分布(见图2).阻塞流状态下，将根据预测断面及与预测断面相邻的上下游断面n时段的交通流参数预测 n+1时段的交通流参数.

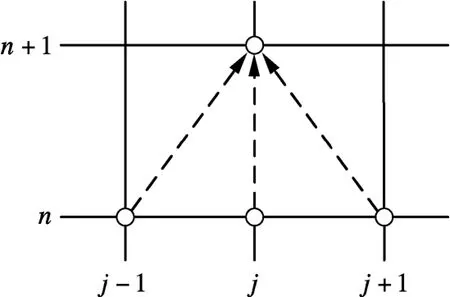
图2 阻塞流状态下守恒方程时空离散节点分布

基于如上假设，设q(x，t)是微分方程(1)的光滑解，将 q(xj，tn+1)在点(xj，tn)处进行 Taylor展开，即

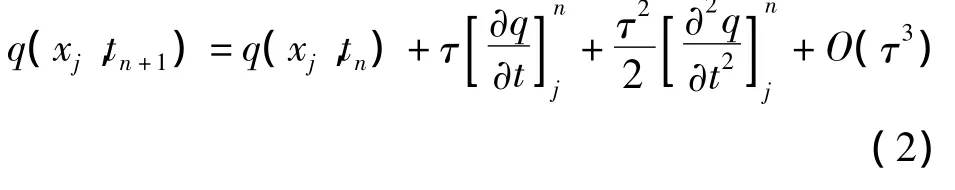
利用假设条件3)及微分方程(1)有

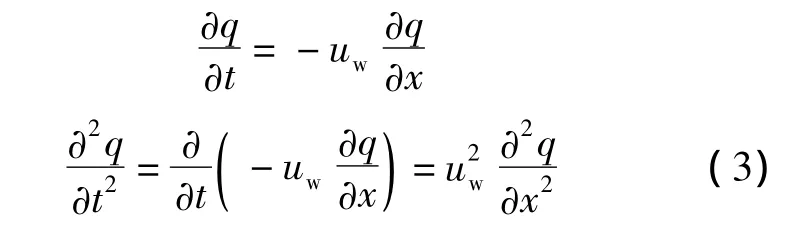
将式(3)代入式(2)，并采用中心差商逼近式(3)中的导数项，同时略去高阶项，可以得到差分格式为

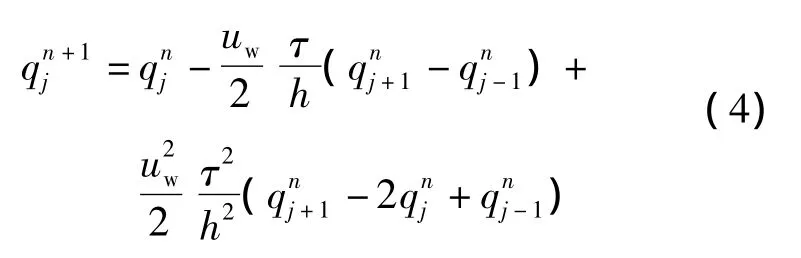
式(4)为二阶精度的Lax-Wendroff差分格式，式(4)表明，n+1时段预测的交通流率不仅与相邻上游断面流量有关，而且与相邻下游断面流量有关.设m断面需要进行交通流短时预测，则上述方程等价于

1.2 有进出口匝道影响的交通流短时预测模型

设t时段在x点处存在侧向驶入、驶出项r和s(其中 r=ri/h，ri为匝道流入率，s=si/h，si为匝道流出率，h为空间离散后路段长度)，令g=r+s，g表示单位时间内净流率.由于驶入、驶出流率的变化势必会影响路段交通流率的变化，为此，在式(5)的基础上引入修正项gn，对gn进行时间和空间离散，由于 r= τri/h，s=τsi/h，所以

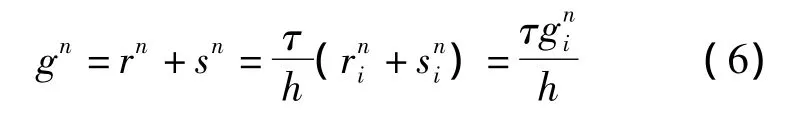
扩展到整个路网，将式(6)代入式(5)，即可得到阻塞流状态下有进出口匝道影响的交通流短时预测模型(矩阵形式)，即

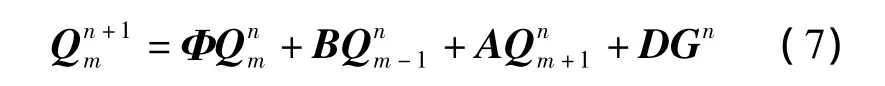
1.3 阻塞流状态下交通流短时预测状态空间模型

进一步考虑道路坡度等影响因素，引入系统噪声Wn，修正后的模型为

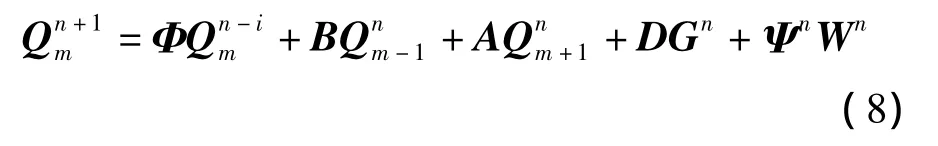
式中，Wn为n时段的系统噪声，定义为均值为零、具有k维方差矩阵Pn的白色噪声;Ψn为噪声转移矩阵;为系统的状态向量;与为系统的输入向量.于是，式(8)就转化为系统状态方程，为达到交通流短时预测的目的，结合交通流参数模型，可构建系统量测方程为

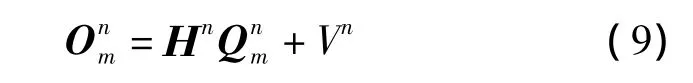
2 基于卡尔曼滤波的状态空间模型求解算法

2.1 交通流短时预测状态空间模型求解算法

1)一步预测方程

一步预测方程是指利用Om和Qm递推计算Qm在n+1时刻的值，即根据m个量测 O1，O2，…，Om对Qm做线性最小方差估计.首先将式(8)与(9)改写为

式(11)即为根据n时刻的状态估计预测n+1时刻状态的一步预测方程，由此可以看出相当于状态一步预测的增益阵.

2)状态估计方程

用一步预测代替真实值引起对量测的估计误差，即

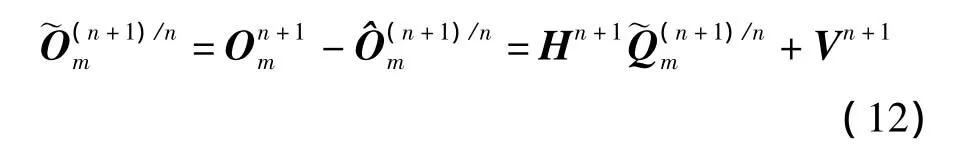
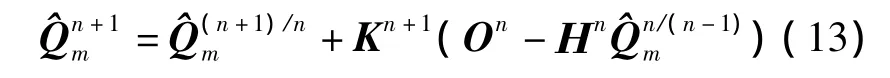
式中，Kn+1为对残差的加权阵，称为滤波增益阵.

3)滤波增益阵和估计均方误差阵

估计均方误差阵为

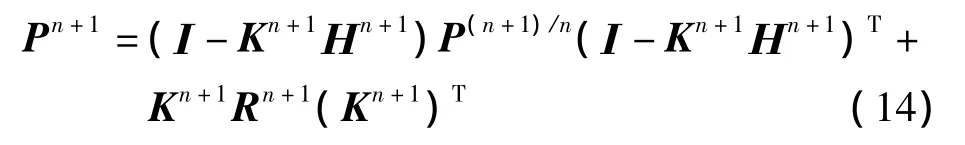
增益阵的选取准则是使估计的均方误差阵达到最小.根据极值原理可从式(14)推导出滤波增益矩阵 Kn+1，即

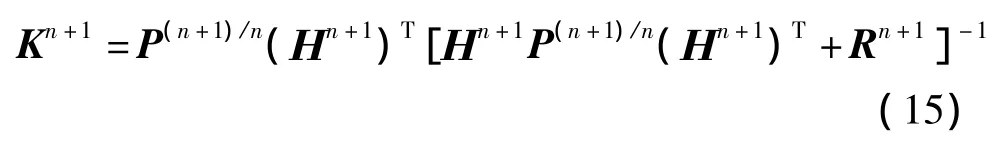
4)一步预测均方误差阵

根据一步预测产生的误差，估计一步预测均方误差阵为

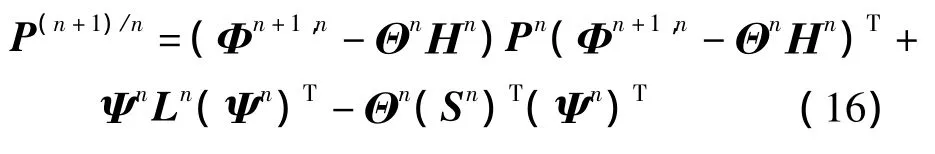
式(16)即为当系统噪声与量测噪声相关时，阻塞流状态下卡尔曼滤波求解算法的一步预测均方误差阵.

2.2 阻塞流状态下交通流短时预测方法及流程

③按照式(15)计算滤波增益阵Kn+1.

⑤依据式(14)，计算估计均方误差Pn+1.

至此，已完成一步预测的全部计算，当系统转至n+1时段，重复①～⑤，即可进行下一时段的预测.上述推导的卡尔曼滤波求解算法与基本卡尔曼滤波方程的主要区别为:

1)卡尔曼滤波求解算法考虑了交通流参数的相关性，在基本卡尔曼递推方程的基础上，求解阻塞流状态下交通流短时预测状态空间模型，实现了交通流短时预测.

3 实证性研究

以北京市某一区域快速路网为研究对象，预测范围如图3所示.实测数据表明:阻塞流状态下，交通流率小于通行能力的55%;占有率大于54%;速度小于30 km/h.由于阻塞流状态属于严重拥堵，且在阻塞流前后易发生交通流状态的改变，因此真正意义上的阻塞流数据非常少，持续的时间也较短.通过对安装在北京市区域路网上20套远程交通微波检测器输出数据的排查，去掉输出数据不足及输出有错误的检测器，以快速路上19个检测器2010年10月一个月内所有工作日的实测数据为基础，通过数据清洗、数据集成、数据转换、数据归约，将数据处理成符合交通流短时预测研究的数据，进行交通流短时预测研究.在数据预处理的基础上，本文选择区域路网内8个同时处于阻塞流状态的断面以1 h为预测时段进行实证性研究.模型验证采用以2 min为采集间隔的远程微波检测器交通流实测数据;预测效果的评价指标采用平均绝对百分比误差(mean absolute percentage error，MAPE)与平均绝对偏差(mean absolute deviation，MAD).

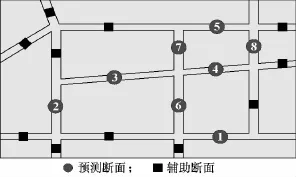
图3 阻塞流状态下预测范围示意图

3.1 模型参数估计

1)交通波波速.当预测时间间隔非常短，预测前后的交通流状态非常相近，则θ2≈90+θ1，而交通波波速 uw=tanθ2= －tanθ1= －uA.因此可根据A点实测的交通流速度负值估计阻塞流状态下交通波波速，如图4所示.

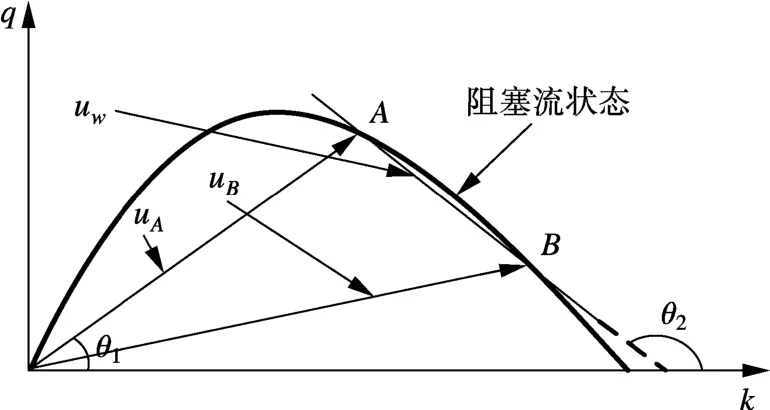
图4 阻塞流状态下交通波波速估算示意图

2)网格比.将交通流守恒方程进行时空离散的过程中采用网格比λ=τ/h'，其中，τ为时间离散步长，h'为空间离散步长，根据网格比的定义，实际交通网络的网格比采用预测时间间隔t与断面之间距离 dij之比，即 λ =t/dij.

3.2 预测效果评价

应用阻塞流状态下交通流短时预测状态空间模型，并采用设计的卡尔曼滤波求解算法，预测阻塞流状态下1 h内的交通流率值，预测效果指标如表1所示.为了比较方法的有效性，采用ARIMA和Elman模型，在相同条件下进行交通流率的预测.应用ARIMA和Elman模型，均需要采用历史数据对模型进行训练，以期找到最优的模型参数，提高模型预测精度.本研究以预测时段前一周的阻塞流数据对ARIMA及Elman模型进行训练.ARIMA模型的参数包括自回归项数、滑动平均项数和使之成为平稳序列所做的差分次数.训练后模型Ljung-Box统计量的显著性值均大于0.05，说明所建立的模型是合理的.由于ARIMA模型仅能实现单断面的预测，因此建立8个ARIMA模型进行预测，预测效果指标如表1所示.在建立ARIMA模型的同时，用训练样本集合对Elman网络模型参数隐层节点数进行标定.Elman网络输入节点为1，输出节点为1，隐层节点数量由试算法确定，根据已有经验，初步设定隐层节点数为2～12，然后用测试样本集合对Elman网络模型进行测试，评价其预测的效果，选择出最优模型.隐层节点数优化结果如表1所示.

阻塞流状态下3种模型预测效果对比表明，卡尔曼滤波算法预测效果最佳，其次为Elman模型，ARIMA模型预测误差相对偏大.本文提出的阻塞流状态下交通流短时预测卡尔曼滤波算法，不仅能实现预测范围内的交通流短时预测，由于同时考虑了时间和空间因素，能够使最大MAPE控制在10%以内;平均MAPE仅为7.96%.虽然Elman模型在断面7处预测平均误差接近卡尔曼滤波算法，但是研究表明当训练样本与实测样本有较大差异时，Elman模型的输出结果将有较大误差.相比于Elman模型，卡尔曼滤波算法预测结果更具鲁棒性.MAPE值对比发现，由于断面1及断面8仅有2个相邻上游断面和一个相邻上游断面，因此卡尔曼滤波算法预测效果不佳.与ARIMA模型相比，卡尔曼滤波算法预测误差远远小于ARIMA模型的预测误差，预测效果明显优于ARIMA模型.以阻塞流状态下交通流短时预测卡尔曼滤波算法预测MAPE最大值和最小值断面为例，对预测值和实测值进行比较，如图5所示.

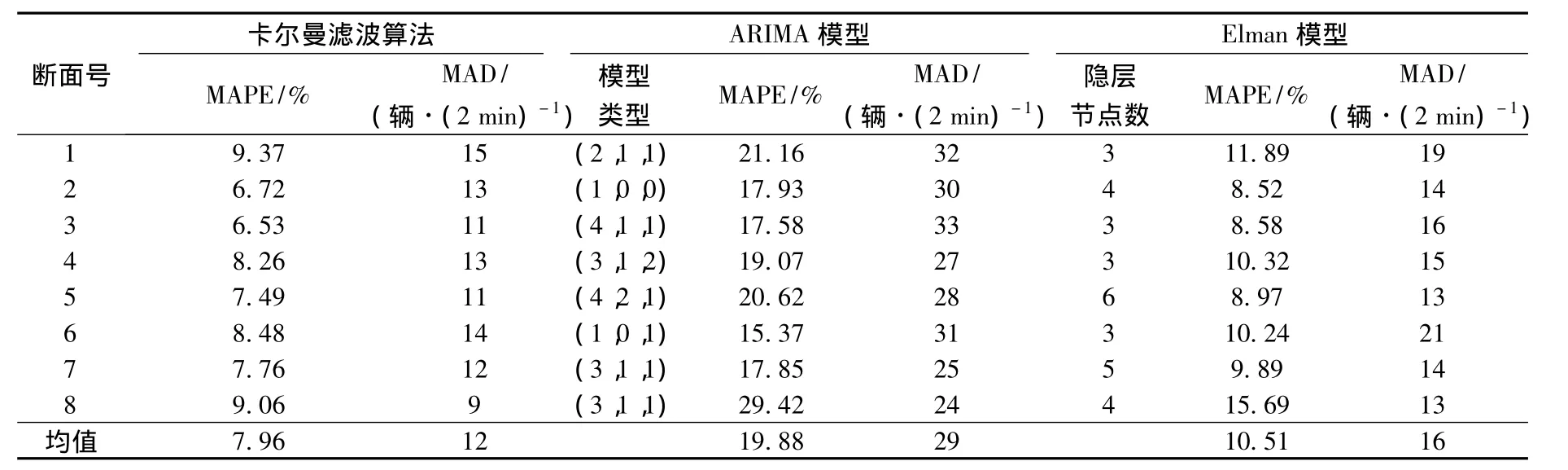
表1 阻塞流状态下交通流短时预测预测效果

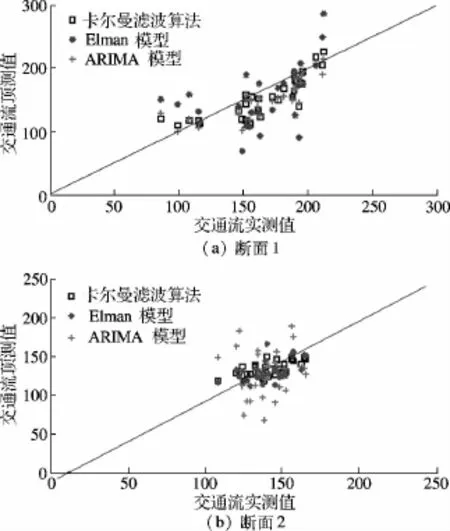
图5 阻塞流状态下交通流短时预测3种模型预测结果

阻塞流状态下，交通流率较大，路段阻抗随之增大，断面之间相对空间距离增加，空间相关性减弱，因此交通流率预测值小于实测值.由图5可以看出，当交通流率过大时，模型的预测结果有偏小的趋势.3种模型预测效果表明，ARIMA模型在实测值较低时，预测值有偏大的趋势;在实测值较高时，预测值有偏小的趋势，总体上，在预测误差相对较大的前提下，预测值趋向实测值均值.Elman模型在实测值与预测值相近的情况下，预测效果较好;实测值与预测值相差较大的情况下，预测效果较差，虽然整体上Elman模型预测效果优于ARIMA模型，但是模型不具备可移植性及鲁棒性.相比于以上2种模型，卡尔曼滤波模型预测效果较好.卡尔曼滤波算法由于考虑了预测断面之间交通流参数空间分布特性，因此各断面预测精度趋于一致.同时，滤波增益矩阵、估计及预测误差阵的存在，能够使预测值根据实测值及预测误差的变化，实时向实测值逼近，预测效果较好，且不需要使用历史数据对模型参数进行训练，具有很好的可移植性及鲁棒性.

4 结语

阻塞流状态下交通流率减小，占有率急剧增加，交通流率和占有率散点图呈直线分布，具有明显的函数关系，因此在分析阻塞流状态下交通流时间和空间特性的基础上，从交通流守恒方程组出发，借鉴偏微分方程求解Lax-Wendroff格式离散思想，考虑阻塞流状态下交通流时间和空间特性以及进出口匝道等因素的影响，建立阻塞流状态下城市快速路网交通流短时预测状态空间模型，并设计了基于卡尔曼滤波方法的模型求解算法.最后，以北京市某一区域路网为例，进行了实证性研究.研究表明，本文建立的阻塞流状态下交通流短时预测卡尔曼滤波算法由于同时考虑了时间和空间因素及交通参数的相关特性，能够使最大MAPE控制在10%以内;平均MAPE仅为7.96%，预测精度优于ARIMA及Elman模型.同时，算法考虑了预测断面之间交通流参数空间分布特性，因此路网内各断面预测精度趋于一致.此外，由于滤波增益矩阵、估计及预测误差阵的存在，能够使预测值根据实测值及预测误差的变化，实时向实测值逼近，预测效果较好，且不需要使用历史数据对模型参数进行训练，具有很好的可移植性及鲁棒性.

References)

[1] Clark S.Traffic prediction using multivariate nonparametric regression[J].Journal of Transportation Engineering，2003，129(2):161-168.

[2] Williams B，Hoel L.Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process:theoretical basis and empirical results[J].Journal of Transportation Engineering，2003，129(6):664-672.

[3] Wang Y，Papageorgiou M.Real-time freeway traffic state estimation based on extended Kalman filter:a general approach[J].Transportation Research Part B，2005，39(2):141-167.

[4] 王建，邓卫，赵金宝.基于改进型贝叶斯组合模型的短时交通流量预测[J].东南大学学报:自然科学版，2012，42(1):162-167.Wang Jian，Deng Wei，Zhao Jinbao.Short-term freeway traffic flow prediction based on improved Bayesian com-bined model[J].Journal of Southeast University:Natural Science Edition，2012，42(1):162-167.(in Chinese)

[5] Smith B L，Williams B M，Oswald R K.Comparison of parametric and nonparametric models for traffic flow forecasting[J].Transportation Research Part C:Emerging Technologies，2002，10(4):303-321.

[6] 张晓利，贺国光，陆化普.基于K-邻域非参数回归短时交通流预测方法[J].系统工程学报，2009，24(2):178-183.Zhang Xiaoli，He Guoguang，Lu Huapu.Short-term traffic flow forecasting based on K-nearest neighbors non-parametric regression[J].Journal of Systems Engineering，2009，24(2):178-183.(in Chinese)

[7] 董春娇，邵春福，李娟，等.基于混沌分析的道路网交通流短时预测[J].系统工程学报，2011，26(3):340-345.Dong Chunjiao，Shao Chunfu，Li Juan，et al.Short-term traffic flow prediction of road network based on chaos theory[J].Journal of Systems Engineering，2011，26(3):340-345.(in Chinese)

[8] 唐铁桥，黄海军.用燕尾突变理论来讨论交通流预测[J].数学研究，2005，38(1):112-116.Tang Tieqiao，Huang Haijun.The discussion of traffic flow forecast by using swallowtail catastrophe theory[J].Journal of Mathematical Study，2005，38(1):112-116.(in Chinese)

[9] 姚智胜，邵春福，熊志华.基于小波包和最小二乘支持向量机的短时交通流组合预测方法研究[J].中国管理科学，2007，15(1):64-68.Yao Zhisheng，Shao Chunfu，Xiong Zhihua.Research on short-term traffic flow combined forecasting based on wavelet package and least square support vector machines[J].Chinese Journal of Management Science，2007，15(1):64-68.(in Chinese)

[10] Castro-Neto M，Jeong Y，Jeong M，et al.Online-SVR for short-term traffic flow prediction under typical and atypical traffic conditions[J].Expert Systems with Applications，2009，36(3):6164-6173.

[11] 董春娇，邵春福，熊志华，等.基于Elman神经网络的道路网短时交通流预测方法[J].交通运输系统工程与信息，2010，10(1):145-151.Dong Chunjiao，Shao Chunfu，Xiong Zhihua，et al.Short-term traffic flow forecasting of road network based on Elman neural network[J].Journal of Transportation System Engineering and Information Technology，2010，10(1):145-151.(in Chinese)

[12] Wahle J，Neubert L，Esser J，et al.A cellular automaton traffic flow model for online simulation of traffic[J].Parallel Computing，2001，27(5):719-735.

[13] May A D.Traffic flow fundamentals[M].New Jersey:Prentice Hall，1990:119-203.

[14] Martin Treiber，Arne Kesting，Dirk Helbing.Threephase traffic theory and two-phase models with a fundamental diagram in the light of empirical stylized facts[J].Transportation Research Part B，2010，44(8/9):983-1000.