导线间串扰对传导骚扰测试的影响

李金龙 马 欣 胡文涛 / 上海市电磁兼容检测重点实验室，上海市计量测试技术研究院

导线间串扰对传导骚扰测试的影响

李金龙 马 欣 胡文涛 / 上海市电磁兼容检测重点实验室，上海市计量测试技术研究院

介绍导线间串扰的理论模型和解析表达式，研究了导线间距离、导线距参考地高度，以及导线半径等参数变化对导线间串扰的影响。通过实验进行验证表明，导线间串扰随着导线间距离的增大而减小，随着导线距参考地高度的增大而增大。最后，为实验室检测和产品设计提出了相应的建议。

电磁兼容；传导骚扰；感性耦合；容性耦合；串扰

0 引言

传导骚扰是指射频电磁能量通过被测设备的外部导线（如电源线，I/O互连线等）被传送出去，对外界产生干扰的传导性电磁骚扰。图1为传导骚扰测试系统示意图，受试设备（equipment under test, EUT）通过测试网络（如人工电源网络AMN，阻抗稳定网络ISN等）将EUT的电磁骚扰能量耦合到测试接收机上。EUT内部或者与EUT互连的导线之间很容易相互耦合产生串扰，影响EUT系统的骚扰发射，测试时会影响到EUT的传导骚扰测试结果及其不确定度。本文研究导线间串扰对测试的影响，首先建立导线间感性耦合与容性耦合的理论模型，确定耦合参数并给出导线间串扰的解析表达式，分析了导线间距离、导线距参考地高度、导线半径等参数变化对导线间串扰的影响。最后，通过实验测试对分析结果进行验证。

图1 传导骚扰测试系统示意图

1 理论模型

在两个导体构成的回路里没有串扰，当加入第三个导体，则会在两个回路之间产生串扰。假设导体上只存在横电磁波传播模式（TEM），便可以方便地建立三导体无损传输线等效模型，如图2所示。

在发射源回路里，由源电压VS（t）和源阻抗RS组成源，通过发射线和参考地与负载RL相连，产生电流IG(z,t)，在发射线与参考地之间产生电压VG(z,t)。受扰回路由近端负载RNE和远端负载RFE通过接收线和参考地相连。发射线产生电磁场在受扰回路里感应出电流IR(z,t)和电压VR(z,t)，其中RNE和RFE上的电压分别为近端电压VNE和远端电压VFE。这里假设为无损耗传输线，即传输线的电阻和电导都忽略不计，则发射源回路与受扰回路之间的寄生参数有：单位长度自电感LG、LR，单位长度互电感Lm，单位长度自电容CG、CR，单位长度互电容Cm，传输线总长为l，则传输线总的互电感为Lml，总的互电容为Cml。

图2 三导体无损传输线等效模型

考虑参考地平面影响时，设两导线距参考地高度相等为h，导线间距离为d，两导线半径相等为r，且r＜＜h，r＜＜d。根据镜像法，可以计算得出两导线间的单位长度互电感和单位长度互电容分别为

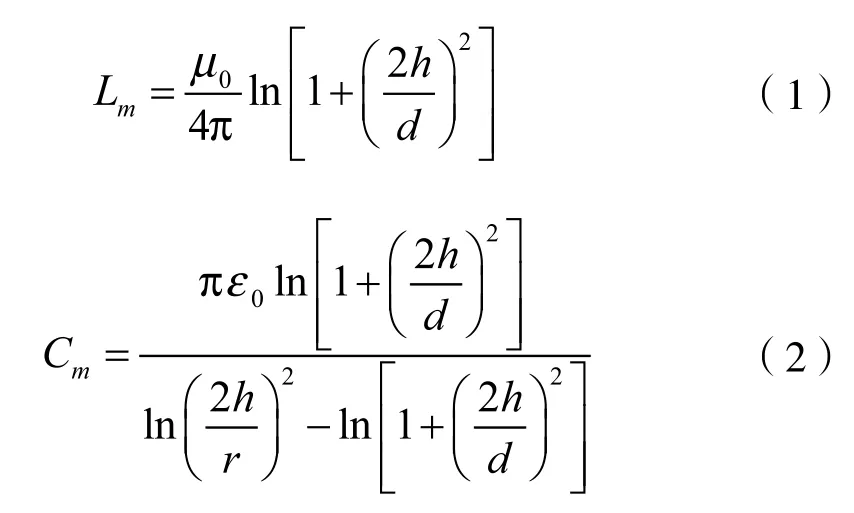
式中：μ0— 真空磁导率；

ε0— 真空介电常数

由式（1）、（2）可知，单位长度互电感Lm与导线间距离d和导线距参考地高度h相关；单位长度互电容Cm与导线间距离d，导线距参考地高度h，以及导线半径r相关。

假设该传输线满足弱耦合条件：（1）传输线发射源VS(t)的波长远远小于传输线时，即l＜＜λ，其中λ=v/f，为发射源的波长；（2）传输线之间是弱耦合的，即忽略受扰回路中感应电流和电压对发射源回路的影响，串扰耦合只是从发射源回路到受扰回路的单向耦合。由法拉第电磁感应定律，受扰回路的磁通量时间变化率在该回路里感应产生两个单位长度的电压源和两个单位长度的电流源，它们分别由受扰回路的自感（或自电容）和互感（或互电容）感应产生，作为一阶模型，忽略自感和自电容的影响，则有互感产生的单位长度电压源VS1=LmdIG/ dt，互电容产生单位长度电流源IS1= -CmdVG/ dt。在频域，用jω代替时间的导数，其中ω= 2πf，f为发射源的频率。则由图2，可以得到近端和远端相量串扰电压分别为

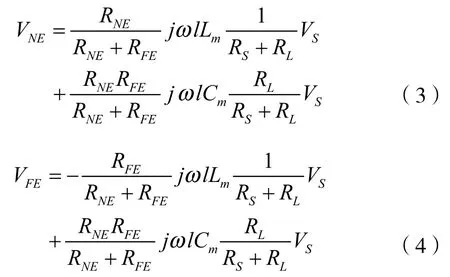
将串扰表示成电压VNE，VFE与VS的比形式，则有近端串扰比函数和远端串扰比函数分别为

两式中，Lm乘积部分为感性耦合部分；Cm乘积部分为容性耦合部分。TNE和TFE分别代表了近端和远端串扰的影响，它们是感性耦合和容性耦合之和。由图2三导体无损传输线等效模型可知，感性耦合可以看作传输线上的一个等效电流源，容性耦合可以看作传输线之间的一个等效电压源，两者在近端负载端电流流向相同，在远端负载端电流流向相反。

2 解析

下文逐点分析了导线间距离、导线距参考地高度，以及导线半径分别对近端和远端串扰比的影响。在式（1）、（2）中，由于真空介电常数（ε0= 8.85 ×10-12F/m）比真空磁导率（μ0= 1.26×10-6H/m）小将近6个数量级，相应的Cm比Lm约小5个数量级。因此，由式（5）、（6）可以看出，终端负载的阻抗大小决定了感性耦合还是容性耦合占优势。即在低阻抗负载回路中，感性耦合占优势，这是因为在低阻抗负载回路中，电流会带来较大影响，而感性耦合是由电流引起的。在高阻抗负载回路中，容性耦合占优势，这是因为在高阻抗负载回路中，电压的影响相对较大，而容性耦合是由电压引起的。在无损传输线模型中，传输线长度和发射源频率只是线性地影响着近端和远端串扰。考虑到实际的测试应用和研究方便，在低阻抗负载回路里进行研究，即假设RS=RL=RNE=RFE= 50 Ω，导线周围介质为空气（即导线为裸线），传输线长度l= 2 m，发射源频率为1 MHz。

2.1 导线间距离的影响

在导线距参考地高度为5 cm，导线直径为1 mm的情况下，分析导线间距离变化对导线间串扰的影响。由式（1）、（2）可以得到单位长度互电感Lm和单位长度互电容Cm随着导线间距离d的变化关系，如图3（a）所示，随着导线间距离的增大，单位长度互电感Lm和单位长度互电容Cm均减小；由式（5）、（6）可以得到近端串扰比TNE和远端串扰比TFE随着导线间距离d的变化关系，如图3（b）所示。由于在低阻抗负载回路中感性耦合占优势，从而决定了近端串扰比TNE和远端串扰比TFE的大小及其变化趋势。由图3（b）可见，随着导线间距离从0.005 m到0.5 m逐渐增大，TNE为正数值，由0.043 34到0.000 26逐渐减小，TFE为负数值，由-0.031 98到-0.000 23逐渐增大。很容易看出TNE和TFE的绝对值|TNE|和|TFE|将会是随着导线间距离的增大而减小，且两者之间的差值为容性耦合部分的2倍。这是由于在低阻抗负载回路里，互电感的变化起主导作用。在其他参数不变的情况下，随着导线间距离的增大，穿过导线的磁通量减小，则互电感随之减小。即导线间串扰随着导线间距离的增大而减小，在导线间距离d≤ 0.1 m范围内，导线间串扰随着距离的增加呈直线趋势急剧减小，而后，当d＞ 0.1 m时，减小的幅度逐渐趋于平缓。

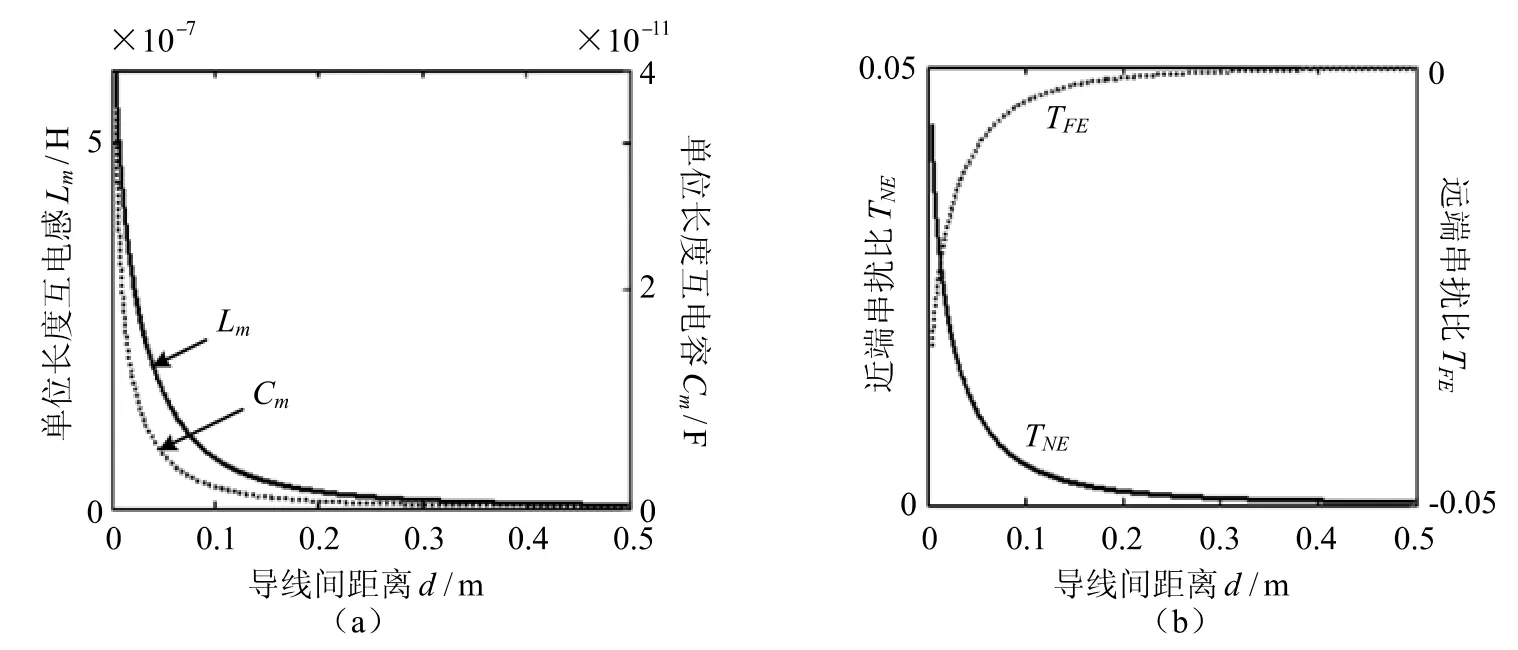
图3 （a）单位长度互电感Lm和单位长度互电容Cm随距离d的变化；（b）近端串扰比TNE和远端串扰比TFE随距离d的变化

2.2 导线距参考地高度的影响

在导线间距离为1 cm、导线直径为1 mm的情况下，分析导线距参考地高度变化对导线间串扰的影响。由式（1）、（2）可以得到Lm和Cm随着导线距参考地高度h的变化关系，如图4（a）所示，随着导线距参考地高度的增大，Lm和Cm均增大；由式（5）、（6）可以得到TNE和TFE随着导线距参考地高度h的变化关系，如图4（b）所示，随着导线距参考地高度从0.005 m到1 m逐渐增大，TNE为正数值由0.004 93到0.074 30逐渐增大，TFE为负数值由-0.003 78到-0.058 86逐渐减小。可以看出TNE和TFE的绝对值|TNE|和|TFE|将会是随着导线距参考地高度的增大而增大，且两者之间的差值仍为容性耦合部分的2倍。这是由于当导线靠近参考地平面时，导线周围磁场会以地平面为中心产生与导线电流方向相反的镜像电流，这样将会降低穿过导线的磁通量。在其他参数不变的情况下，随着导线距参考地高度的增大，镜像电流对穿过导线磁通量的抵消作用减小，则磁通量增大，互电感随之增大。即导线间串扰随着导线距参考地高度的增大而增大，在导线距参考地高度h≤0.4 m范围内，导线间串扰以较快的幅度增大，而后，当h＞ 0.4 m时，增大的速度逐渐变慢。

图4 （a） 单位长度互电感Lm和单位长度互电容Cm随参考地高度h的变化；（b）近端串扰比TNE和远端串扰比TFE随参考地高度h的变化

2.3 导线半径的影响

在导线间距离为1 cm、导线距参考地高度为5 cm的情况下，分析导线半径变化对导线间串扰的影响。导线半径的变化只会影响到单位长度互电容Cm，即导线半径的变化只影响到容性耦合部分，与感性耦合部分无关。由式（2）可以得到，Cm随着导线半径r的变化关系，如图5（a）所示，Cm随着导线半径的增大而增大；由式（5）、（6）可以得到TNE和TFE随着导线半径r的变化关系，如图5（b）所示，随着导线半径的增大，TNE为正数值由0.031到0.044逐渐增大，TFE为负数值也以相同的变化趋势由-0.027到-0.014逐渐增大。可以看出TNE的绝对值|TNE|将会随着导线半径的增大而增大，TFE的绝对值|TFE|将会随着导线半径的增大而减小，两者之间的差值同样为容性耦合部分的2倍。即近端串扰影响随着导线半径的增大而增大，远端串扰影响随着导线半径的增大而减小。

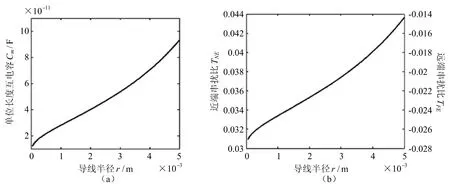
图5 （a） 单位长度互电容Cm随半径r的变化；（b）近端串扰比TNE和远端串扰比TFE随半径r的变化

3 实验

根据以上的解析结果，在实验上对此进行验证。如图6所示为导线间串扰实验系统的原理图，在实验实施中结合实际，选取了导线间距离变化和导线距参考地高度变化进行分析。在低阻抗回路中，分别在频率f= 0.5 MHz、1 MHz、5 MHz、10 MHz时，对远端串扰电压进行实验测量。

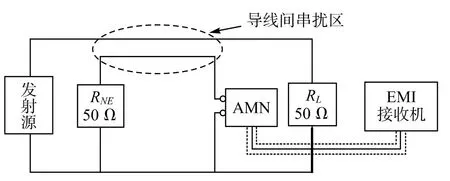
图6 导线间串扰实验系统原理图

在导线距参考地高度、导线半径等参数一定的情况下，远端串扰电压随着导线间距离的变化关系，如图7所示。可见，随着导线间距离增大，远端串扰电压逐渐减小，远端串扰的比值也随之减小。图7中（i）所示为远端串扰电压与发射源电压的比值随着导线间距离的变化关系。当导线间距离相等时，频率为1 MHz、5 MHz、10 MHz的远端串扰比随着频率的增大而非线性地增大，频率为0.5 MHz的远端串扰比在导线间距离大于10 cm之后大于频率为1 MHz的远端串扰比。这是由于公共接地阻抗，实验中的传输线损耗，以及波长远小于传输线尺寸限制条件等因素引起的。

在导线间距离、导线半径等参数一定的情况下，远端串扰电压随着导线距参考地高度的变化关系，如图8所示。可见，随着导线距参考地高度增大，远端串扰电压逐渐增大，远端串扰的比值也随之增大。图8中（i）所示为远端串扰电压与发射源电压的比值随着导线距参考地高度的变化关系，当导线距参考地高度相同时，远端串扰比随着频率的增大也是非线性地增大。

图7 远端串扰电压随着导线间距离的变化

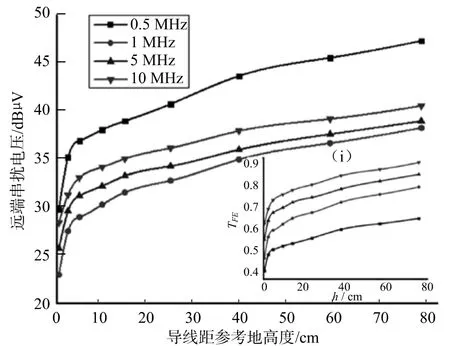
图8 远端串扰电压随着导线距参考地高度的变化

由以上分析可以看出，导线间距离、导线距参考地高度，以及导线半径对导线间串扰都有影响，其中，导线间距离和导线距参考地高度的影响尤为明显。实际应用中，导线与导线之间的距离不能太近，应尽量互相远离，导线距参考地高度应尽量低，在满足应用需求的前提下尽量缩短互联导线的长度。在实施检测当中的样品布置时，应严格按照标准要求，如样品之间的距离应保持典型距离为10 cm，导线距参考面的距离或者高度为40 cm以上等要求，同时，还要注意不同功能的导线尽量不要绕在一起等，以减小可能影响测试结果的因素。

4 结语

本文通过导线间串扰的等效模型和解析表达式，研究了导线间距离、导线距参考地高度，以及导线半径等参数变化对导线间串扰的影响。研究表明，在无损传输线模型中，传输线长度和发射源频率只是线性地影响着近端和远端串扰。在低阻抗负载回路里，感性耦合占据优势，从而决定着近端和远端串扰的大小和变化趋势。导线间串扰随着导线间距离的增大而减小，随着导线距参考地高度的增大而增大。由于导线半径的变化只影响到容性耦合，与感性耦合无关，因此在感性耦合占优势的情况下，随着导线半径的增大，容性耦合增大，从而近端串扰增大，远端串扰减小。

实际的应用中，由于公共接地阻抗，以及导线本身阻抗等影响，导线间串扰的响应曲线会有一定的误差，特别是在较高发射源频率的情况下，这种误差尤为明显。但是，本文在较低发射源频率条件下的无损传输线假设是合理的，并已通过实验室测试对分析的结果进行了验证，实验表明两者结果相吻合。这将为保证实验室测试数据一致性，以及电子产品的电磁兼容设计提供一定的参考。

[1] [美] Clayton R Paul.电磁兼容导论[M]. 闻映红，译. 北京: 人民邮电出版社, 2007: 367-456.

[2] Wolfgang J R Hoefer. The Transmission-Line Matrix Method-Theory and Applications[J]. IEEE Transactions on Microwave Theory and Techniques, 1985, 33(10): 882-893.

[3] 倪光正. 工程电磁场原理[M]. 北京：高等教育出版社, 2009: 81-98.

[4] Clayton R Paul. Solution of the Transmission-Line Equations Under the Weak-Coupling Assumption[J]. Electromagnetic Compatibility, 2002，44(3): 413-423.

[5] 高印寒, 王瑞宝, 李碧若, 谢军, 杨开宇. 汽车线束电感性串扰动态变化的预测[J]. 光学精密工程, 2011, 19(5): 1088-1094.

[6] International Electrotechnical Commission. CISPR16-2-1: 2010 [S]. Geneva，2010.

Impact of crosstalk in wires to conducted emission measurement

Li Jinlong, Ma Xin, Hu Wentao
（Shanghai Key Laboratory of Electromagnetic Compatibility Test, Shanghai Institute of Measurement and Testing Technology）

In this paper, the theory model and analytical expressions of crosstalk in wires are introduced. The effects of distance between two wires and height of wires to reference ground and wire radius are discussed. Verification experiments show that the crosstalk in wires increases with the distance between two wires decreasing or the height of wires to reference ground increasing. Meanwhile, corresponding suggestions were posed for laboratory tests and product design.

EMC; conducted emission; inductive coupling; capacitive coupling; crosstalk