信号调制关联噪声驱动下光学双稳系统的瞬态性质分析
2014-03-14何丽萍
桂 堤,何丽萍,熊 辉
(湖北理工学院 数理学院,湖北 黄石 435003)
平均首次通过时间(mean first passage time,MFPT)是随机动力学理论研究中的一个重要课题,用来描述非线性系统的瞬态特性,已成为人们广泛关注的研究课题。游敬云[1]等研究了乘法噪声系数对双稳锯齿系统逃逸率的影响;王兵[2]等研究了双色噪声驱动非对称双稳系统平均第一穿越时间;宁丽娟[3]等研究了色关联噪声驱动的非对称双稳系统中平均首次穿越时间;王国威[4]等研究了关联噪声和周期信号驱动非对称双稳系统的稳态分析。
在之前的众多研究当中,只考虑了噪声的各种关联形式对系统的影响。由于噪声也受信号的影响,考虑噪声受信号的调制与实际更加吻合,而在此之前的研究讨论噪声受信号调制后对系统的影响较少。本文将讨论受周期信号调制的白关联的乘性噪声与加性白噪声驱动下光学双稳系统的平均首次通过时间问题。
1 双稳系统的平均首次通过时间
考虑如下乘性白噪声和加性白噪声驱动的光学双稳系统[5]:
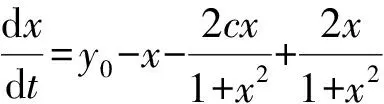
(1)
式(1)中,c为双稳参数,y0为激光输入模,x为激光输出模,ξ(t)、η(t) 分别为乘性噪声和加性噪声。设驱动系统的乘性噪声ξ(t)受到周期信号Bcos(Ωt)的调制, 则有:
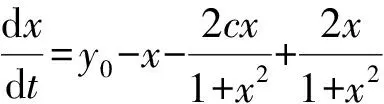
(2)
且ξ(t)、η(t) 满足如下统计性质[6]:
〈ξ(t)〉=〈η(t)〉=0,
〈ξ(t)ξ(t')〉=2Qδ(t-t')=γ11,
〈η(t)η(t')〉=2Dδ(t-t')=γ22,

(3)
式(2)~(3)中,B代表调制信号幅值,Ω代表调制信号频率,Q代表泵噪声ξ(t)的强度,D代表量子噪声η(t) 的强度,λ代表噪声间的关联强度,为一常量。
通过求解方程(1)~(3)可以得到该系统的福克-普朗克方程如下[7]:
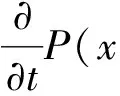
(4)

由方程(4)求得系统的稳态概率密度函数为:
(5)

U(x)=-Q[u(x)+v(x)+w(x)+z(x)]
(6)
式(5)~(6)中:





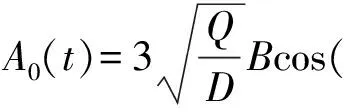
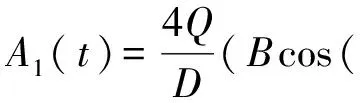
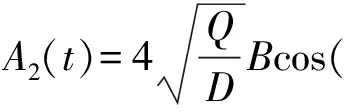


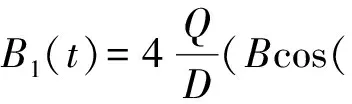


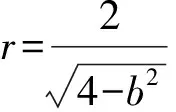


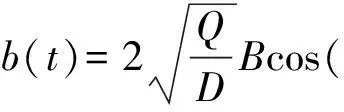

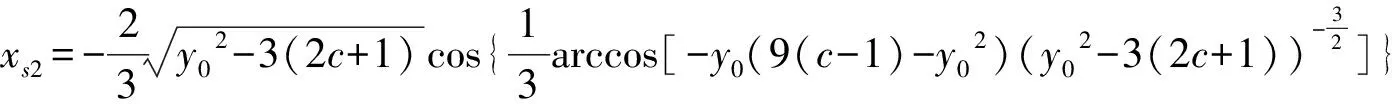
(7)
式(7)中,xs1和xs2代表稳定点,xu代表不稳定点。
利用平均首次通过时间的定义和最陡下降法可得2个不同方向的平均首次通过时间的表达式为[5-8]:


(8)


(9)
式(8)~(9)中,V(x),B(x),U(x)及xs1,xs2,xu均与前文中定义相同。
2 各参量对平均首次通过时间的影响
利用2个不同方向的平均首次通过时间的表达式(8)和(9),讨论各参量分别对T+(xs1→xs2)和T-(xs2→xs1)的影响。
不同双稳参数c的取值对平均首次通过时间T+(xs1→xs2)和T-(xs2→xs1)随输入信号振幅B的变化曲线的影响如图1所示,其他参数为:y0=6.07,λ=1,Q=3,D=2,Ω=0.001。从图1(a)中可以看出, 在小B(B<0.6)范围内, 平均首次通过时间T+(xs1→xs2)随B值的增大迅速减小并趋于零, 在0.4

(a) T+(xs1→xs2)随B的变化曲线

(b) T-(xs2→xs1)随B的变化曲线
不同输入信号振幅B的取值对平均首次通过时间T+(xs1→xs2)和T-(xs2→xs1) 随加性噪声强度D的变化曲线的影响如图2所示,其他参数为:c=4.95,λ=1,y0=6.07,Ω=0.001,Q=3。从图2(a)中可以看出,平均首次通过时间T+(xs1→xs2)随D值的增大逐渐增大。随着B值的增大,曲线整体朝D值增大的方向移动。固定D, 可以发现,平均首次通过时间T+(xs1→xs2)随B值的增大而减小。这说明D和B对系统从稳态xs1到另一个稳态xs2所起的作用刚好相反,即B越大或D越小,系统从稳态xs1到另一个稳态xs2所用的平均时间均越短。从图2(b)中可以看出, 平均首次通过时间T-(xs2→xs1)随D值的增大先增大后减小,即出现一个极大值。随着B值的增大,曲线朝D值增大的方向移动,且极大值逐渐降低。这说明D和B对系统从稳态xs2到另一个稳态xs1所起的作用不同,即随D值的增大, 系统从稳态xs2到另一个稳态xs1所用的平均时间先变长后变短,B值越大,系统从稳态xs2到另一个稳态xs1所用的平均时间越短。
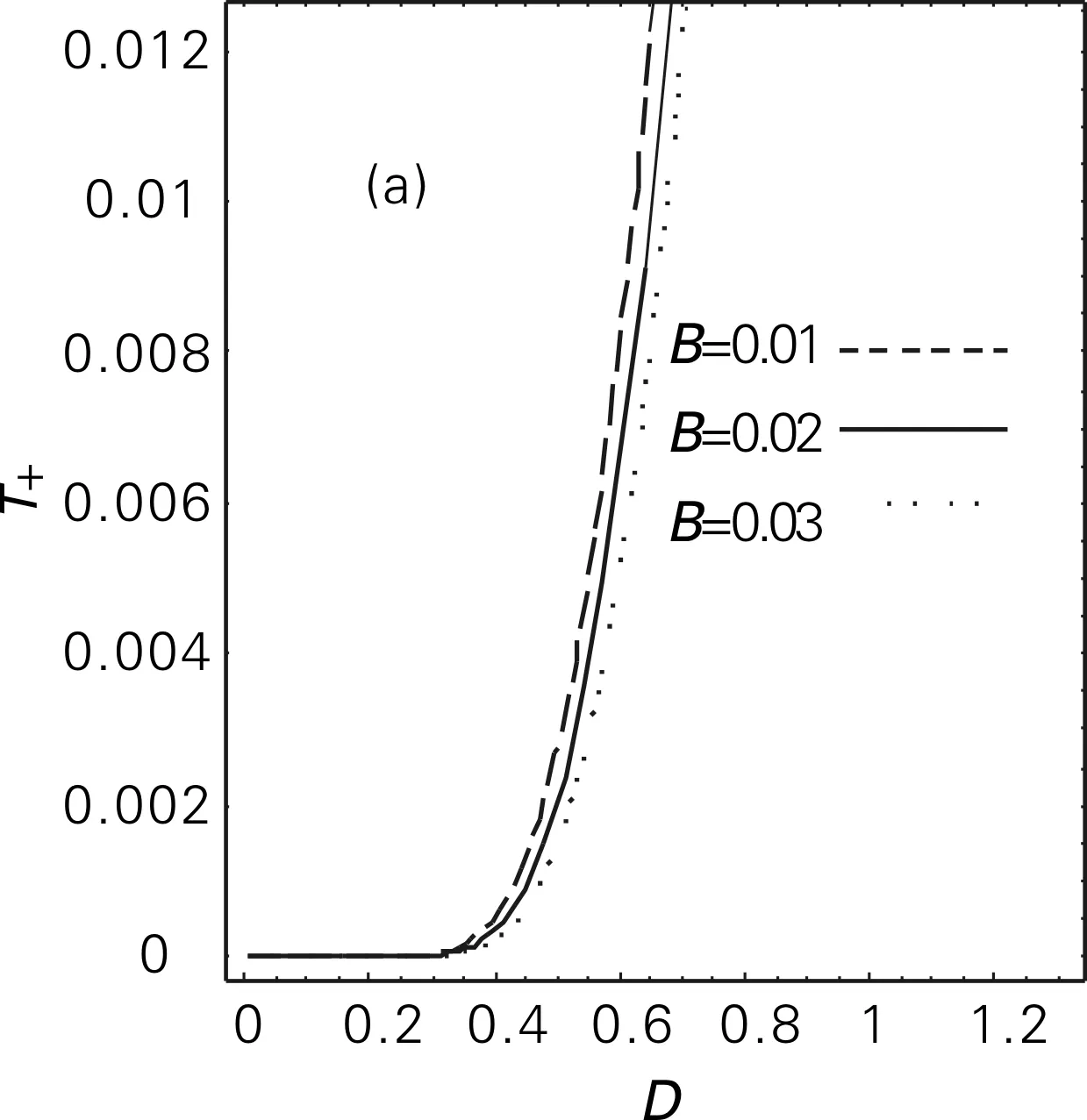
(a) T+(xs1→xs2)随D的变化曲线
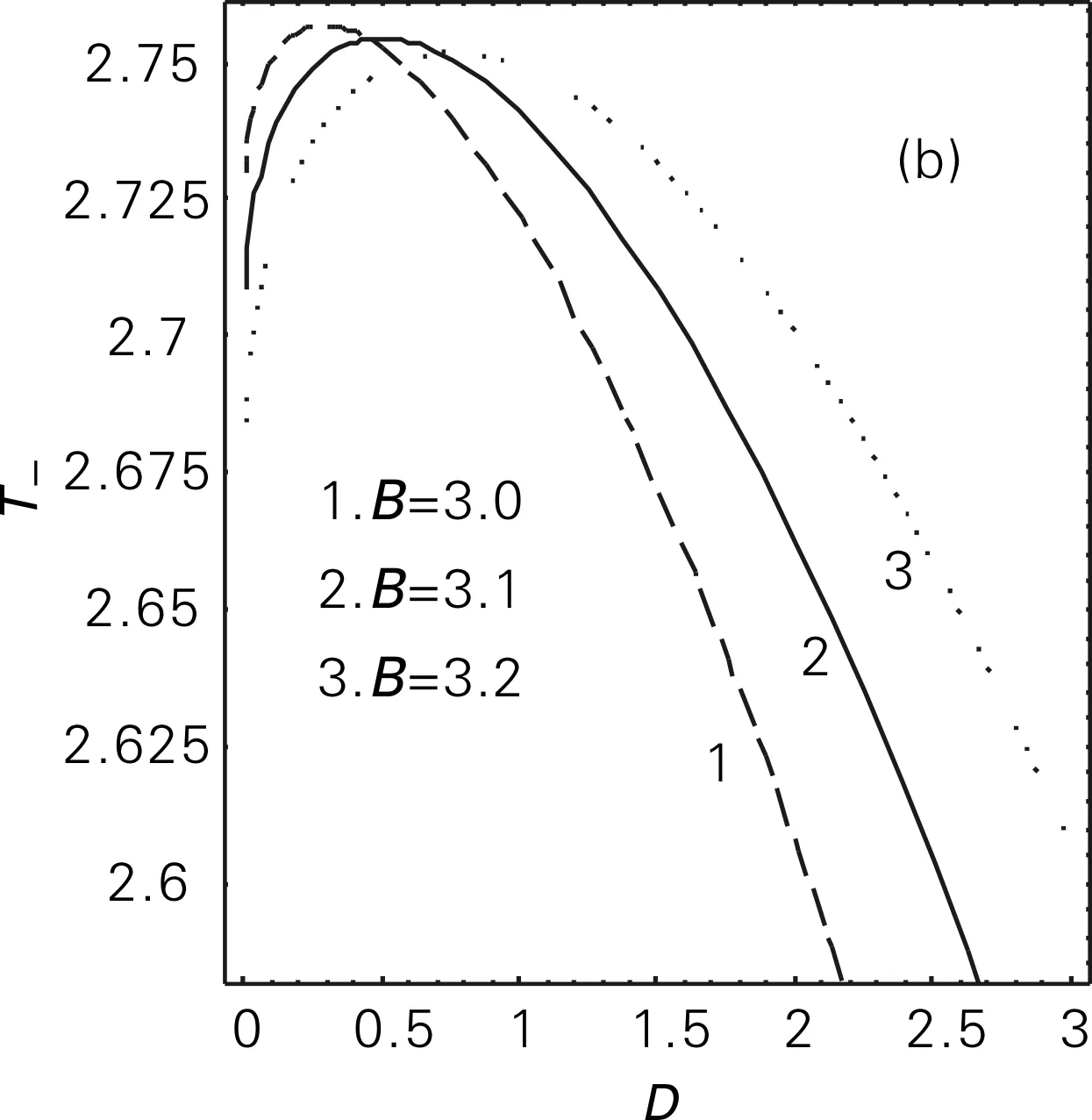
(b) T-(xs2→xs1)随D的变化曲线
不同输入信号振幅B的取值对平均首次通过时间T+(xs1→xs2)和T-(xs2→xs1)随输入信号频率Ω的变化曲线的影响如图3所示,其他参数为:c=4.95,λ=1,y0=6.07,D=2,Q=3。从图3(a)中可以看出,平均首次通过时间T+(xs1→xs2)随Ω作周期性等振幅的振荡,随着B值的增大,振荡的幅值也增大, 但振荡的周期和振荡的平衡位置均不变。从图3(b)中可以看出,平均首次通过时间T-(xs2→xs1)随Ω出现周期性多峰振荡,随着B值的增大,振荡的峰值逐渐增大,但峰值的位置不变。

(a) T+(xs1→xs2)随Ω的变化曲线
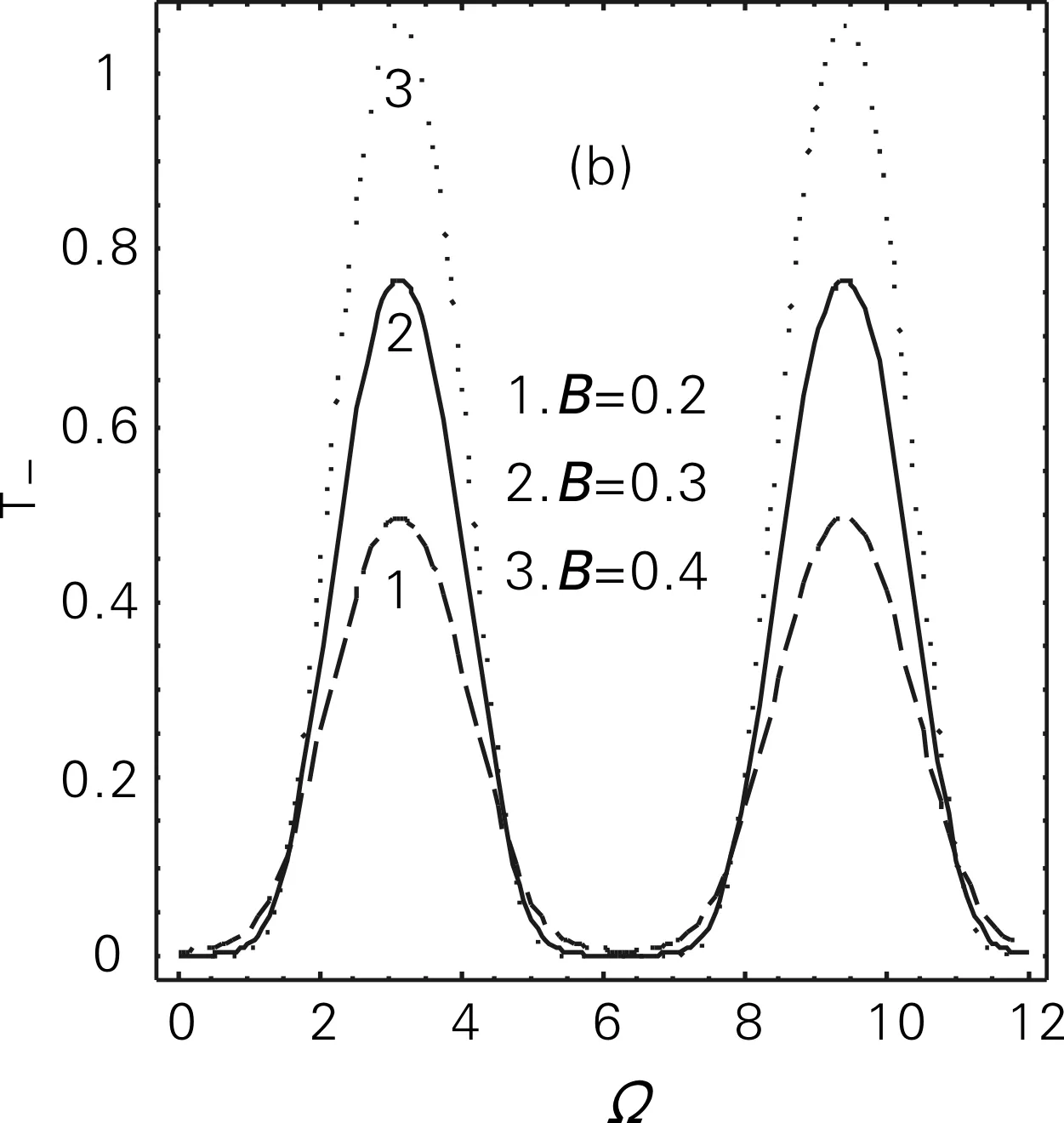
(b) T-(xs2→xs1)随Ω的变化曲线
比较图3(a)和图3(b)可以看出,Ω对系统从稳态xs1到另一个稳态xs2和系统从稳态xs2到稳态xs1所起的作用不同,而B对系统从稳态xs1到另一个稳态xs2和系统从稳态xs2到稳态xs1所起的作用相同,即系统从稳态xs1到另一个稳态xs2所用的平均时间随Ω作周期性等振幅振荡,系统从稳态xs2到另一个稳态xs1所用的平均时间随Ω作周期性多峰振荡;B值越大,系统从稳态xs1到另一个稳态xs2和系统从稳态xs2到稳态xs1所用的平均时间均越长。
3 结 论
本文研究了信号调制关联噪声驱动下光学双稳系统的平均首次通过时间问题, 在得到2个方向的平均首次通过时间的表达式的基础上,讨论了各个参量对平均首次通过时间的影响。研究发现:①T+(xs1→xs2)和T-(xs2→xs1)均随B值的增大先迅速减小并趋于零,接着保持不变,且中间出现间断点,然后迅速增大,最后逐渐减小,即出现一个极大值。②T+(xs1→xs2) 随c值的增大,曲线整体下移,且峰的位置向B值增大的方向移动。T-(xs2→xs1)随c值的增大,曲线先整体上移后整体下移,但峰的位置基本不变。③T+(xs1→xs2)随D值的增大单调上升,T-(xs2→xs1)随D值的增大出现一个极大值。④T+(xs1→xs2)随Ω作周期性等振幅的振荡,T-(xs2→xs1)随Ω出现周期性多峰振荡。
参考文献
[1] 游敬云,曹力,吴大进,等.乘法噪声系数对双稳锯齿系统逃逸率的影响[J].华中科技大学学报(自然科学版),2001,29(2):108-110.
[2] 王兵,吴秀清,邵继红.双色噪声驱动非对称双稳系统平均第一穿越时间研究[J].物理学报,2009,58(3):1391-1395.
[3] 宁丽娟,徐伟,杨晓丽.色关联噪声驱动的非对称双稳系统中平均首次穿越时间的研究[J].物理学报,2007,56(1):25-29.
[4] 王国威,程庆华,徐大海.关联噪声和周期信号驱动非对称双稳系统的稳态分析[J].量子电子学报,2014,31(1):86-93.
[5] 于占东.色关联噪声驱动的双稳系统在两个方向上的平均首通时间的研究[D].昆明:云南大学,2008.
[6] 靳艳飞,徐伟,马少娟,等.非对称双稳系统中平均首次穿越时间的研究[J].物理学报,2005,54(8):3480-3485.
[7] 杨建华,刘先斌.色交叉关联噪声作用下癌细胞增长系统的平均首通时间[J].物理学报,2010,59(6):3718-3732.
[8] 于占东,赵自保,曾春华,等.色关联噪声驱动双稳系统平均首通时间的研究[J].云南大学学报(自然科学版),2009,31(5):493-498.
