基于D-P准则巷道围岩力学响应特征分析
2014-03-14马海峰徐遵玉冯吉成张科学
马海峰,徐遵玉,冯吉成,张科学
(1.中国矿业大学(北京) 资源与安全工程学院,北京 100083;2 中国煤炭科工集团 重庆研究院,重庆 400000)
岩体开挖后,破坏了原有岩体自身的应力平衡状态,应力将重新分布。重新分布的应力往往会超过岩体的屈服强度,致使巷道周边的部分围岩进入塑性状态,随着距巷道轴线的径向距离的增大,围岩将由塑性状态向弹性状态过渡,使巷道围岩出现弹塑性状态并存的应力分布特点[1]。随着煤矿开采深度的增加,原岩应力不断升高,巷道所处的地质环境和应力环境更加复杂。许多学者对巷道开挖后围岩的力学特征进行了研究。高富强等[2]研究了巷道围岩分区破裂化现象。谢广祥等[3]通过对综放面回采巷道围岩的深部位移、表面位移、应力分布以及支架荷载的实测分析,得出综放面回采巷道围岩力学特征分布规律。常聚才等[4]通过对深部岩巷开挖后围岩应力演化特征、变形破坏规律的分析,揭示了深井岩巷围岩稳定性控制机理。王永岩[5]对深部工程中不同深度的巷道围岩在高地应力作用下的蠕变破坏过程进行了数值模拟,应用Mohr-Coulomb和Griffith破坏准则获得了高地应力岩体的蠕变破坏规律。李德海[6]利用ANSYS对圆巷的黏弹性模型位移场进行了数值模拟分析。黄先伍[7]以圆形巷道为例分析了巷道毛洞或均匀支护、局部支护或局部弱支护时围岩内应力的解析解,得出了圆形巷道整体及局部支护时围岩的弹塑性应力场分布。谢和平[8]综述了深部高地应力条件下岩石的强度特征以及岩石的破坏特征。
以往研究中应用较多的Mohr-Coulomb准则和Hoke-Brown准则都忽略了中间主应力的作用[9],据实验结果分析[10],中间主应力的影响在15%左右。Druker-Prager(D-P)准则是在Mohr-Coulomb准则和塑性Mises准则的基础上扩展而得到的,计入了中主应力的影响,又考虑了静水压力的作用,克服了Mohr-Coulomb准则和Hoke-Brown准则的不足。为获得考虑中间主应力的巷道围岩的力学特征,本文基于D-P准则分析了不同侧压系数下巷道围岩的应力、塑性区半径的解析解,并与基于Mohr-Coulomb准则的计算结果进行对比分析,讨论了D-P准则和Mohr-Coulomb准则的计算结果对巷道稳定性的影响。采用COMSOL Multiphysics中的岩土力学模块模拟了巷道围岩开挖后的力学响应特征。
1 力学模型
为简化分析,需做以下基本假设:深埋巷道为圆形、无限长巷道;原岩为理想弹塑性体;原岩为不可压缩材料。巷道半径为a,处于垂直应力为p0、水平应力均为λp0的应力状态。
由于巷道轴线方向的尺寸远远大于巷道断面的另外两个方向的尺寸,可将巷道围岩应力状态的弹塑性简化为平面应变问题分析[10]。围岩应力分析的力学模型如图1所示。
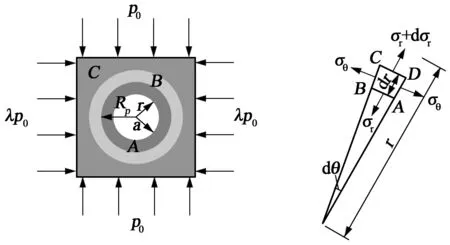
A—塑性区;B—弹性区;C—原岩应力区图1 力学模型
1.1 弹性区应力
在弹性区内,距巷道轴线为r处围岩的径向应力为σr,切向应力为σθ,剪切应力为τrθ,其弹性解为基尔希解[11]:
(1)
1.2 塑性区应力
图1所示的微单元体处于塑性平衡状态,建立平衡微分方程,化简为:
(2)
Druker-Prager准则的表达式为:
(3)
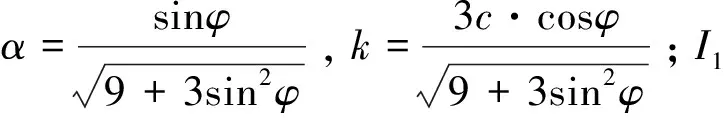
工程中常用中间主应力系数n来反映中间主应力σ2与最大主应力σ1和最小主应力σ3的关系,其表达式为:
(4)
由于σ1≥σ2≥σ3,所以0≤n≤1。
由式(4)可得
σ2=nσ1+(1-n)σ3
(5)
则
I1=σ1+σ2+σ3=(1+n)σ1+(2-n)σ3
=m2(σ1-σ3)2
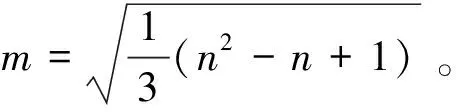
于是Druker-Prager准则的表达式可写为:
(m-nα-α)σ1-(m-nα+2α)σ3-k=0
(6)
在巷道周边围岩中,由于巷道断面上的径向应力σr、切向应力σθ和巷道轴向应力σz两两正交,一般σθ最大,σr最小,于是可认为:σ1=σθ,σ2=σz,σ3=σr。
于是式(6)可写为:
(m-nα-α)σθ-(m-nα+2α)σr-k=0
(7)
由(7)可得:
(8)
为方便计算,令
将式(2)化简、积分得:
lnr=-ln(σθ-σr)+C
(9)
式中,C为积分常数,由边界条件可确定。
将式(8)代入式(9),可解得:
(10)
将塑性区内边界条件r=a,σr=pi,pi为巷道支护阻力,代入式(10)可得:
将C代入式(10),再代入式(8)、(5)可得巷道支护阻力为pi时的塑性区应力:
(11)
(12)
(13)
1.3 塑性区半径
当应力超过围岩的屈服极限强度后巷道围岩出现塑性区,随着径向距离r的增大,巷道围岩将由塑性状态过渡到弹性状态,在弹塑性交界处既满足弹性应力条件,又满足塑性应力条件,即弹塑性区内两应力之和相等。
σθ+σr=2p0
(14)
(15)
联立式(14)、(15)可得塑性区半径
(16)
2 算例与讨论
为得到基于D-P准则下巷道围岩的应力分布特征,以淮南矿业集团谢一煤矿为例,具体参数取值如下:p0= 15MPa,E=39GPa,u=0.23,φ=35°,C=3.1MPa。图2为基于D-P准则和Mohr-Coulomb准则下巷道围岩应力分布曲线。
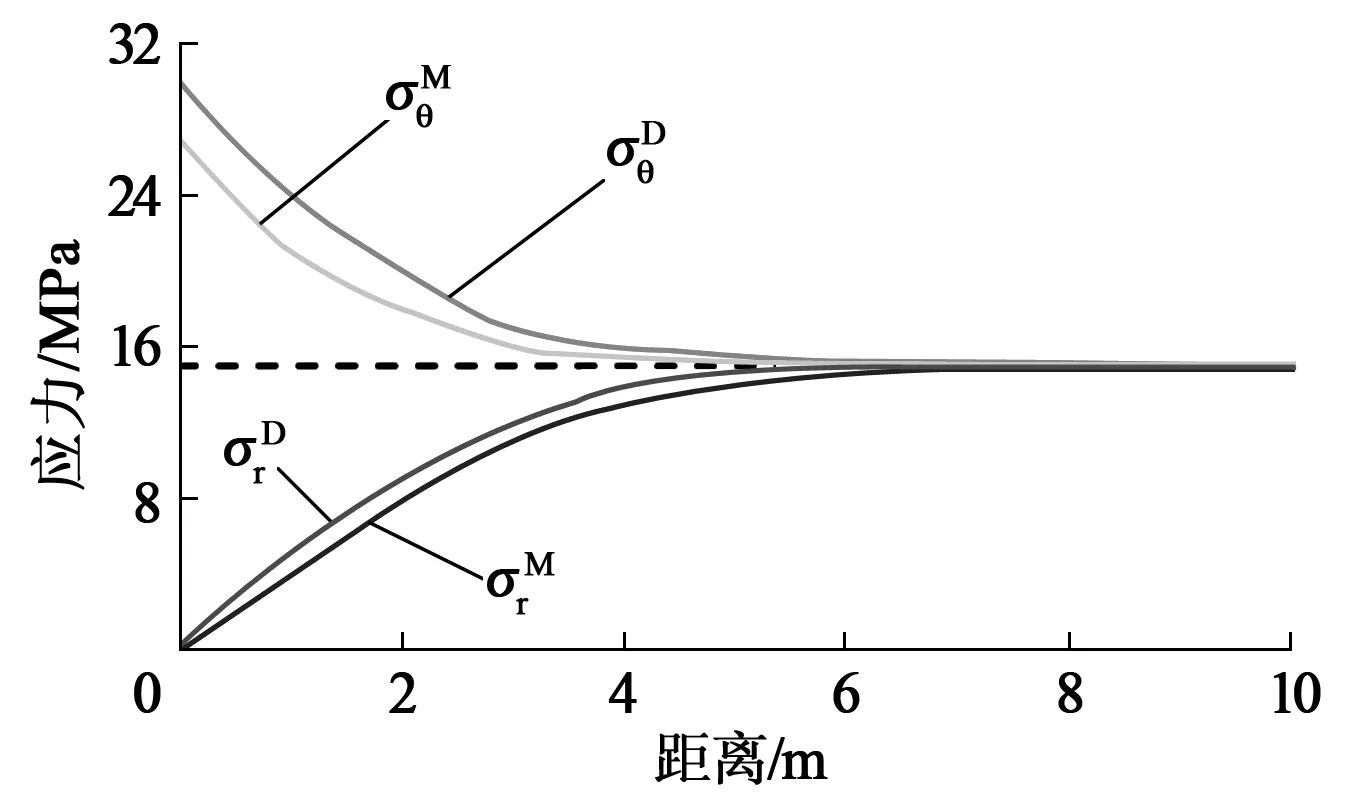
图2 巷道围岩应力分布曲线
由图2可知,基于D-P准则的巷道围岩应力分布曲线与典型的巷道围岩应力分布特征一致,基于D-P准则得到的切向应力最大为29.8MPa,而基于Mohr-Coulomb准则的切向应力最大为27.2MPa。可见,基于Mohr-Coulomb准则的应力值偏小,在进行巷道支护设计时会使设计支护强度偏小,降低巷道围岩的稳定性,容易造成对巷道围岩失稳破坏的低估。
3 巷道围岩力学特征数值模拟
为获得不同侧压系数下巷道开挖后围岩力学特征,本文以淮南矿业集团谢一矿的地质资料为背景,采用COMSOL Multiphysics中的岩土力学模块,模拟巷道开挖后无支护时,巷道围岩应力场、位移场及塑性变形区分布特征。数值模拟采用的煤岩体力学参数如表1所示。
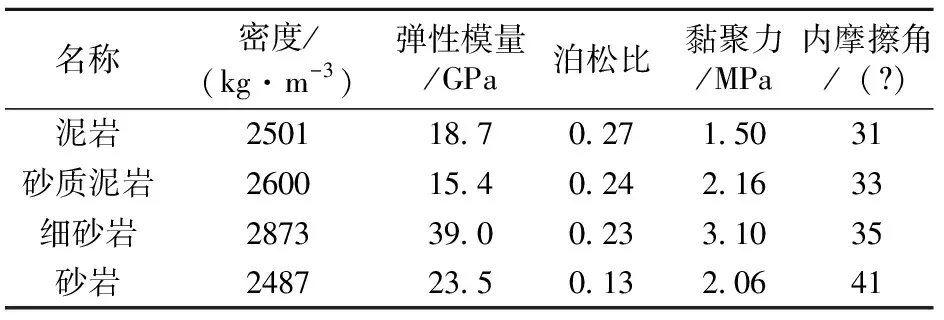
表1 煤岩体力学参数
3.1 巷道围岩应力场
图3为侧压系数与最大垂直应力的关系。
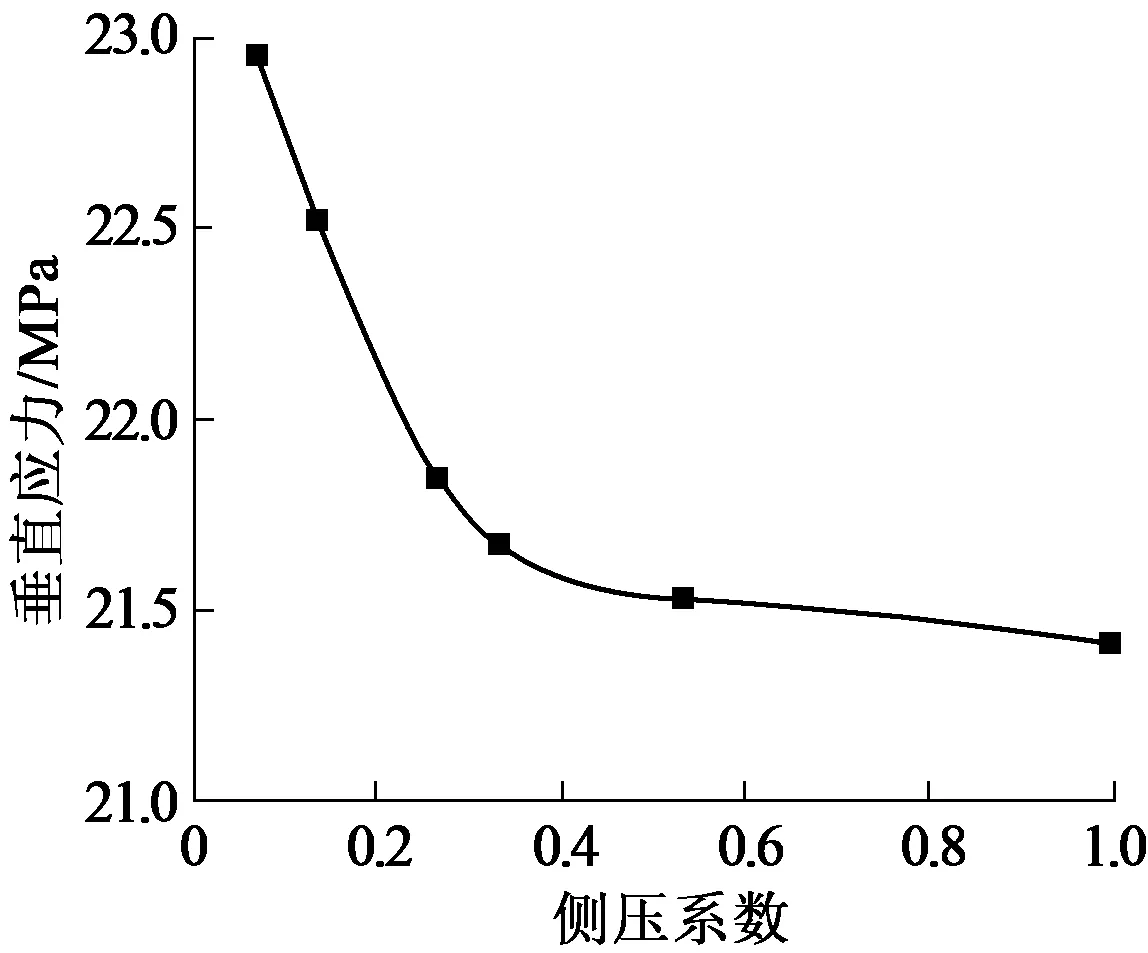
图3 侧压系数与最大垂直应力的关系
模拟结果表明,围岩开挖后,巷道周围应力场呈现对称性分布,在巷道周边围岩形成应力集中区和应力降低区,顶底板形成明显的应力降低区,巷道底板出现拉应力,巷道两侧围岩形成应力集中区。由图3可以看出,侧压系数λ由0.1增大至1时,应力峰值逐渐减小,应力集中程度亦逐渐减小,λ=0.1时最大垂直应力为22.96MPa,应力集中系数为1.53,λ=0.5时最大垂直应力为21.54MPa,应力集中系数为1.44,λ=1时最大垂直应力为21.42MPa,应力集中系数为1.43。
当侧压系数0.1<λ<0.5时,应力减小幅度较大,巷道围岩应力受侧压系数的影响较明显,围岩应力对侧压系数的敏感性较大;当侧压系数0.5<λ<1时,应力减小幅度较小,巷道围岩应力受侧压系数的影响不明显,围岩应力对侧压系数的敏感性较小。
由剪应变能理论可知:应力较高处的围岩聚集了大量能量,当积聚的能量超过某一临界值时就会使围岩发生破坏同时能量得以释放,若积聚的能量在瞬间得到释放,很可能诱发事故。因此,围岩在开挖后应及时进行支护,尤其是侧压系数较小的巷道。
3.2巷道围岩位移场
图4为侧压系数与最大垂直位移的关系。

图4 侧压系数与最大垂直位移的关系
模拟结果表明,巷道围岩位移场呈对称性分布,侧压系数λ<1时,随着侧压系数的增大,垂直位移量逐渐减小,顶板下沉量和底板底鼓量逐渐减小,产生垂直位移的范围亦逐渐减小。当侧压系数0.1<λ<0.5时,位移量减小幅度较大,巷道围岩位移受侧压系数的影响较明显,围岩位移对侧压系数的敏感性较大;当侧压系数0.5<λ<1时,位移量减小幅度较小,巷道围岩位移受侧压系数的影响不明显,围岩位移对侧压系数的敏感性较小。
3.3 巷道围岩塑性变形区
图5为侧压系数λ=0.1,λ=0.5,λ=1的巷道围岩塑性变形区云图。
由图5可知:围岩开挖后在巷道周边形成了一定范围的塑性变形区,塑性变形区对称、均匀分布。在塑性区围岩出现了较大的塑性变形,围岩的力学指标弹性模量、黏聚力、内摩擦角由于围岩的破坏而降低。侧压系数λ<1时,随着侧压系数的增大,巷道围岩塑性变形区逐渐减小。
塑性变形区是围岩开挖后应力场在一定时间和空间上重新分布的结果。当围岩集中应力超过围岩的屈服极限强度时,围岩便由弹性状态转变为塑性状态,产生了永久性塑性变形,形成塑性变形区,并且塑性变形区由巷道表面围岩向深部围岩扩展,塑性变形量随着向深部围岩扩展逐渐减小,至原岩应力区时,变形量减为0,围岩由塑性区依次过渡到原岩应力区。当集中应力达到围岩强度极限后,围岩发生破坏并进入峰后残余状态,可由巷道两侧破坏的围岩得到证实。



图5 塑性变形区
4 现场验证
淮南谢一煤矿一水平运输大巷采用原设计支护巷道时,围岩变形严重,尤其是顶底板位移量较大,影响了煤炭的正常运输和行人安全。由上述算例的参数可知侧压系数λ=0.3,λ介于0.1~0.5之间,采用D-P准则计算的切向应力为21.55MPa。
为提高巷道稳定性,并结合该条件下采用D-P准则计算的切向应力值,对巷道支护参数进行了改进,采用强力锚杆、锚索组合支护,支护参数为:锚杆为直径25mm的左旋无纵筋锚杆,长度2.4m,极限破断力超过400kN,锚杆间距800mm,排距1.0m。顶板锚索钻孔直径28mm,树脂端部锚固后施加预应力,然后其余部分采用水泥浆全长锚固,锚索排距1.2m,间距900mm。锚索托板为300mm×300mm×16mm高强托板,采用钢筋网护帮护顶。
提高支护强度前后,对巷道围岩位移量进行了监测,监测结果如图6所示。
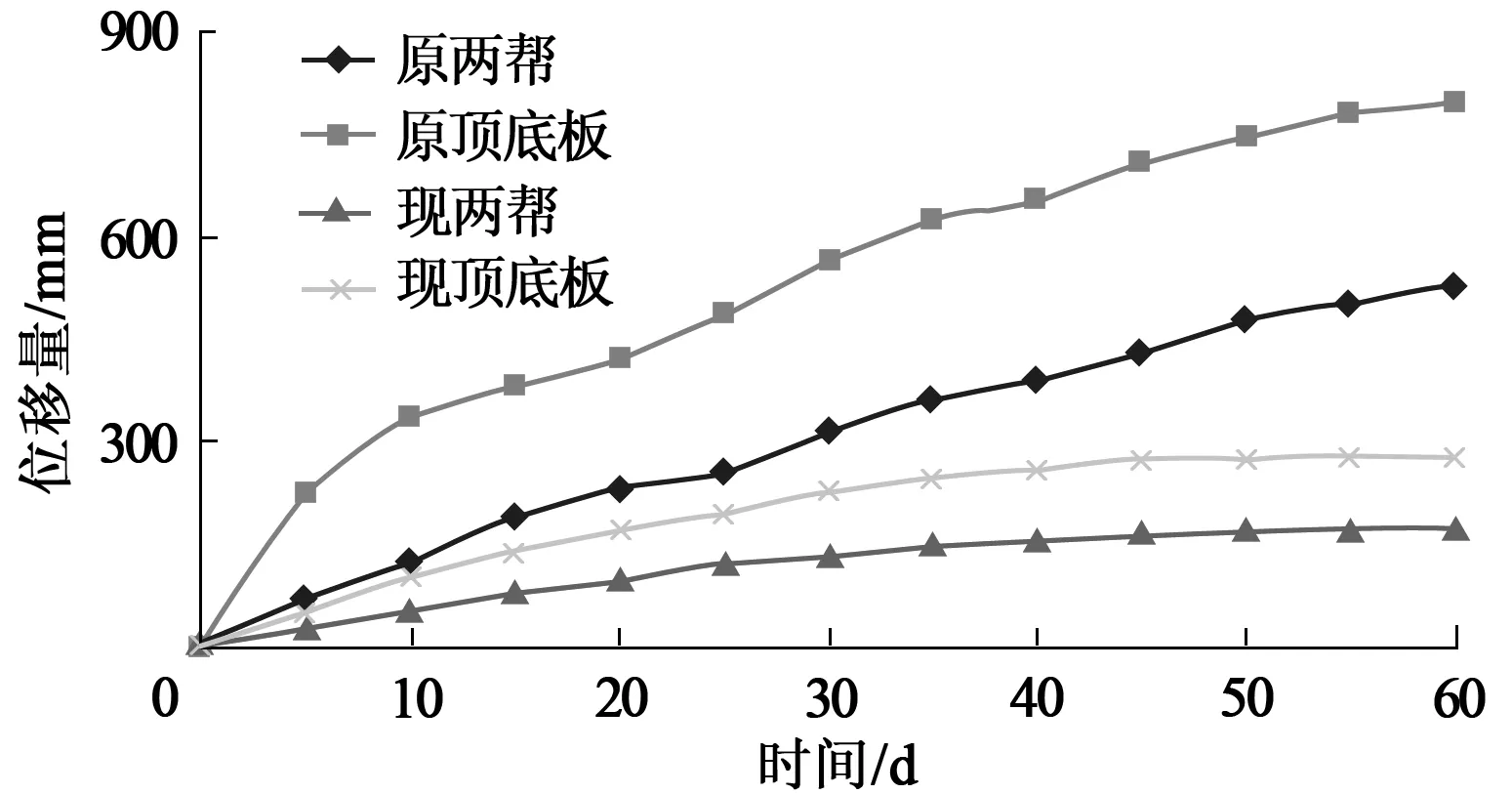
图6 巷道围岩位移曲线
由图6可知,提高巷道支护强度后,围岩位移量明显减小,巷道围岩得到了有效控制,稳定性较好,进而说明了基于D-P准则计算得到的围岩应力较符合实际情况。
5 结束语
(1)基于D-P准则得到的巷道围岩应力分布曲线与典型的围岩应力分布特征一致,而基于Mohr-Coulomb 准则计算的应力值偏小,使设计支护强度偏小,容易造成对巷道围岩失稳破坏的低估。
(2)巷道开挖后围岩应力场、位移场呈对称性分布,当侧压系数λ<1时,随着λ的增大,应力峰值和应力集中程度逐渐减小,垂直位移量和垂直位移场范围亦逐渐减小。
(3)当侧压系数0.1<λ<0.5时,巷道围岩应力和位移减小幅度较大,应力和位移受侧压系数的影响较明显,对侧压系数的敏感性较大;当侧压系数0.5<λ<1时,巷道围岩应力和位移减小幅度较小,应力和位移受侧压系数的影响不明显,对侧压系数的敏感性较小。
(4)巷道围岩开挖后在巷道周边形成了塑性变形区,塑性变形区呈对称性分布;侧压系数λ<1
时,随着侧压系数的增大,巷道围岩塑性变形区逐渐减小。
[参考文献]
[1]侯公羽.岩石力学基础教程[M].北京:机械工业出版社,2010.
[2]高富强,康红普,林 健.深部巷道围岩分区破裂化数值模拟[J].煤炭学报,2010,35(1):21-25.
[3]谢广祥,杨 科,常聚才.综放回采巷道围岩力学特征实测研究[J].中国矿业大学学报,2006,35(1):94-98.
[4]常聚才,谢广祥.深部巷道围岩力学特征及其稳定性控制[J].煤炭学报,2009,34(7):881-886.
[5]王永岩,齐 珺,杨彩虹,等.深部岩体非线性蠕变规律研究[J].岩土力学,2005,26(1):117-121.
[6]李德海,王东攀,高保彬.围岩黏弹性模型有限元模拟分析[J].矿冶工程,2005,25(1):1-3.
[7]黄先伍.巷道围岩应力场及变形时效性研究[D].徐州:中国矿业大学,2008.
[8]周宏伟,谢和平,左建平.深部高地应力下岩石力学行为研究进展[J].力学进展,2005,35(1):91-99.
[9]周小平,钱七虎,杨海清.深部岩体强度准则[J].岩石力学与工程学报,2008,27(1):117-123.
[10]沈明荣,陈建峰.岩体力学[M].上海:同济大学出版社,2006.
[11]钱鸣高,石平五.矿山压力与岩层控制[M].徐州:中国矿业大学出版社,2003.
[12]张志强,关宝树.软弱围岩隧道在高地应力条件下的变形规律研究[J].岩土工程学报,2000,22 (6):696-700.
