时变时延和非时延耦合的复杂网络自适应同步

巩长忠，蔡晓东

（中国民航大学理学院，天津 300300）

时变时延和非时延耦合的复杂网络自适应同步

巩长忠，蔡晓东

（中国民航大学理学院，天津 300300）

研究了2个带有时变时延和非时延耦合的复杂网络自适应同步问题，其中耦合矩阵不要求一定是对称矩阵或不可约的。分别对具有相同和不同拓扑结构的网络进行了研究，基于Lyapunov稳定性理论，得到了几种使2个复杂网络同步的充分条件。最后，数值模拟结果验证了方法的有效性。

复杂网络；同步；时变时延；非时延；耦合

复杂网络的同步问题一直是许多应用领域的研究焦点之一，目前主要研究网络的拓扑结构及其动力学行为。而在诸多现实问题中，网络节点之间存在着不可忽略的时间延迟，因此，许多文献中都研究了带有延迟的复杂网络同步问题。

利用网络状态和线性矩阵不等式的方法，得到带有时延耦合复杂网络同步的条件[1]，通过一些限制条件，来保证驱动系统和响应系统的误差渐进稳定性，就可以使驱动响应系统在一般意义上达到同步[2]，这些研究都集中在了网络内同步问题。对于带有时延和非时延的复杂网络，通过自适应控制器得到了广义同步的一些充分条件[3]，自适应同步的结果还可反应到实践中的动力学行为上来[4]。这些研究考虑的时延都是定值，但在实际问题中，时间延迟有时是一个时变函数，使系统更加复杂难以解决。

基于以上讨论及Lyapunov稳定性理论，研究了带有时变时延和非时延的复杂网络同步问题，证明了可通过控制器的设计实现2个复杂网络的同步，且对于耦合矩阵，不要求配置矩阵是对称或不可约的。文中首先描述了问题模型，然后设计了控制器并给予证明，最后数值仿真也验证了方法的有效性。

1 问题描述

假设一个复杂网络有N个节点，每个节点是n维子系统，其模型表示如下

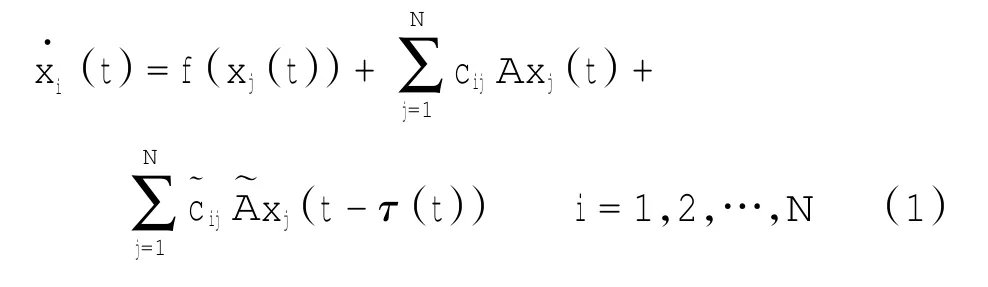
式（1）为驱动系统，带有自适应控制器的响应系统模型为

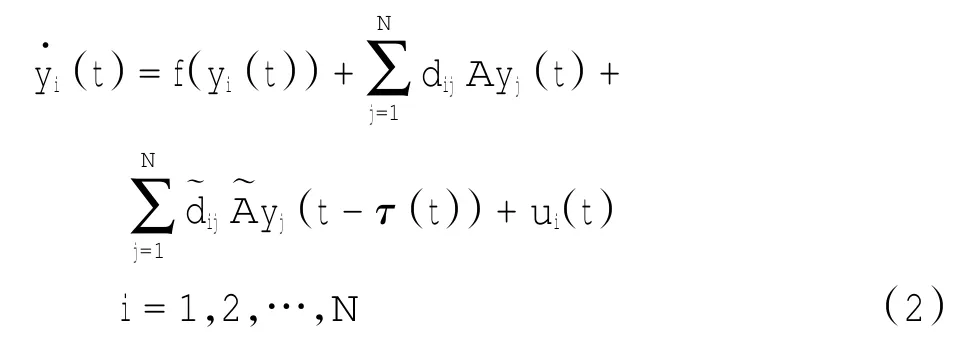
其中：yi（t）=（yi1（t），yi2（t），…，yin（t））T∈Rn为响应系统第i个节点的状态向量；D=（dij）N×N∈RN×N为响应系统网络拓扑结构的外部耦合矩阵；函数f和矩阵A与系统（1）中意义相同；ui（t）为第i个节点的控制器。

系统（1）和（2）的初始条件为

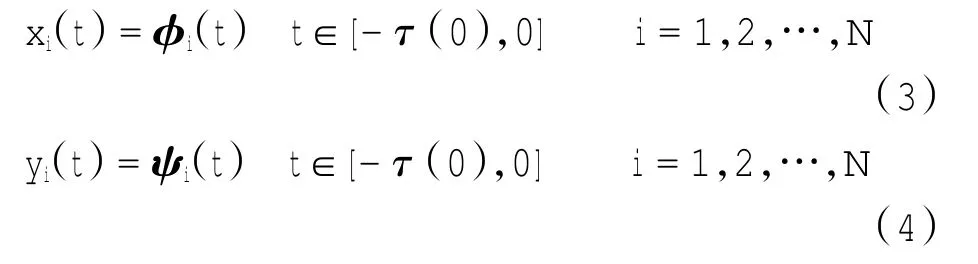
其中：φi（t）和ψi（t）是定义在t∈[-τ（0），0]上的连续可微的向量函数。

定义1 假设xi（t；t0；φi）和yi（t；t0；ψi）（i=1，2，…，N）是系统（1）和（2）的解，其中φi=φi（t）∈C（[-τ（0），0]，Rn）和ψi=ψi（t）∈C（[-τ（0），0]，Rn）是初始条件，f∶R×Ω→Rn是连续可微的，Ω⊆Rn。若存在一个非空集Λ⊆Ω，φi在Λ上取值，使得xi（t；t0；φi）∈Ω，则对于任意t≥t0，i=1，2，…，N有

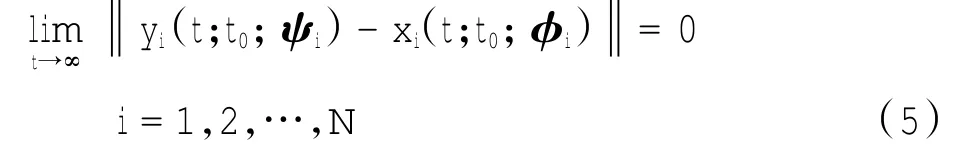
其中：‖·‖表示的是2-范数，则称系统网络（1）和（2）达到同步。

假设1 f（·）∈Rn满足利普西斯条件，即存在一定值L使得

引理1 对于任意向量x，y∈Rn和可逆正定矩阵Q∈Rn×n，以下矩阵不等式成立[5]

定义误差向量

可得误差系统

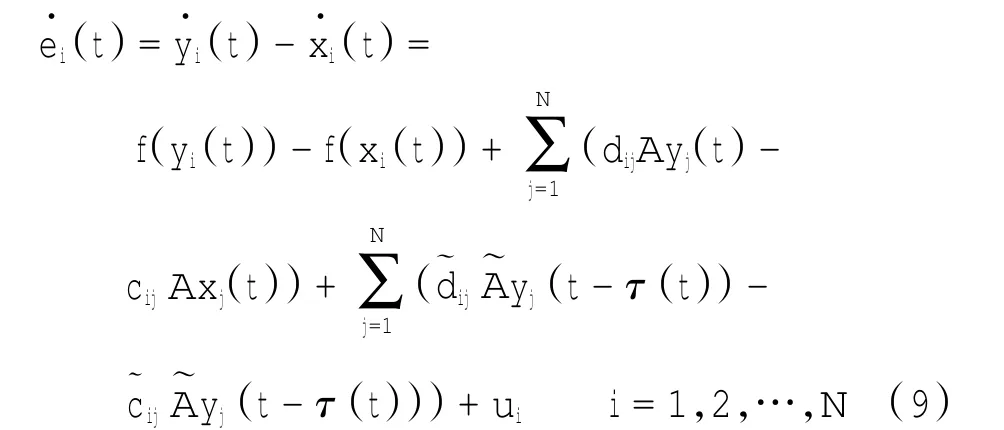
显然系统（1）和（2）的网络同步问题等同于误差系统（9）的零解的稳定性问题。

2 主要结论

定理1 假设1成立，在不同的配置条件下，使得控制器设计如下，驱动系统（1）和响应系统（2）可达到网络同步。即

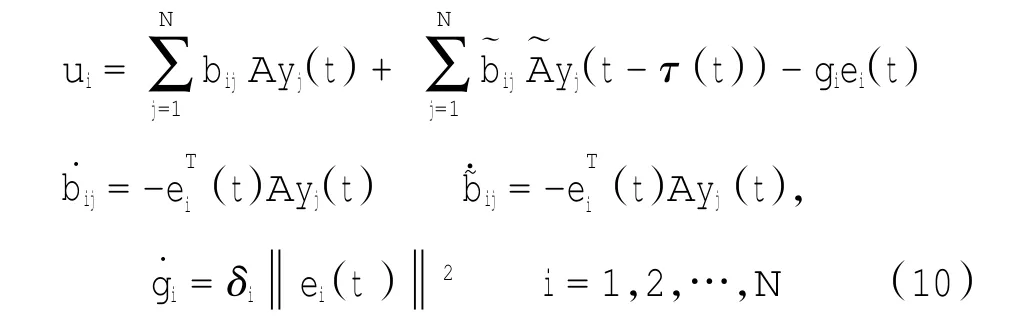
其中：δi是正常数。

证明构造Lyapunov函数

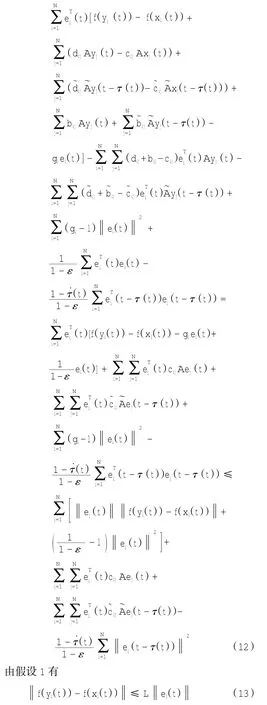
由引理1可推导出

注释1 控制器（10）中常数δi（i=1，2，…，N）的取值会影响网络同步速度，取值越大，同步速度越快。

推论1 假设1成立，驱动系统（1）和响应系统（2）未达到网络同步，控制器可设计为

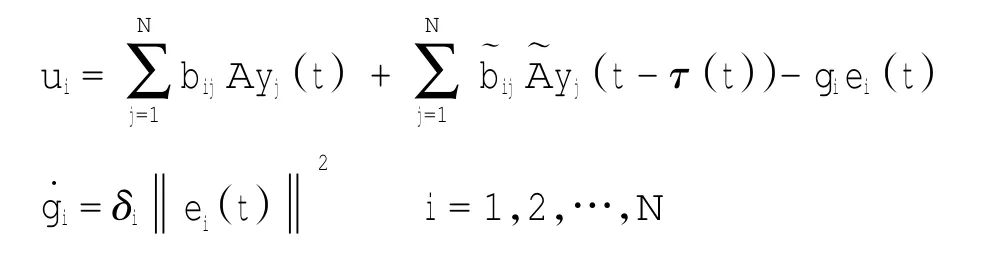
其中：δi是正常数，i=1，2，…，N。

推论2 假设1成立，驱动系统（1）和响应系统（2）有相同的配置，使则使两个复杂网络同步的控制器可设计为

其中：δi是正常数。

3 数值仿真

使用Matlab进行数值仿真来证明该方法的有效性。为简单起见，考虑6个节点组成的网络系统。对于f（x）选用Chaotic Lorenz系统[6-7]

其中：i=1，2，…，6；a=10；b=8/3；c=28；对于Chaotic Lorenz系统来说，满足假设1的条件，对任意xi和xj存在一常数r使下式成立

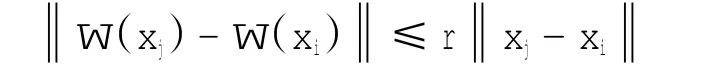
图1给出了误差系统的仿真结果。图中ei1（t）、ei2（t）、ei3（t）为两网络系统同步轨道的误差，由图可知误差ei1（t）、ei2（t）、ei3（t）迅速收敛到0，也就是说，两系统达到了网络同步。

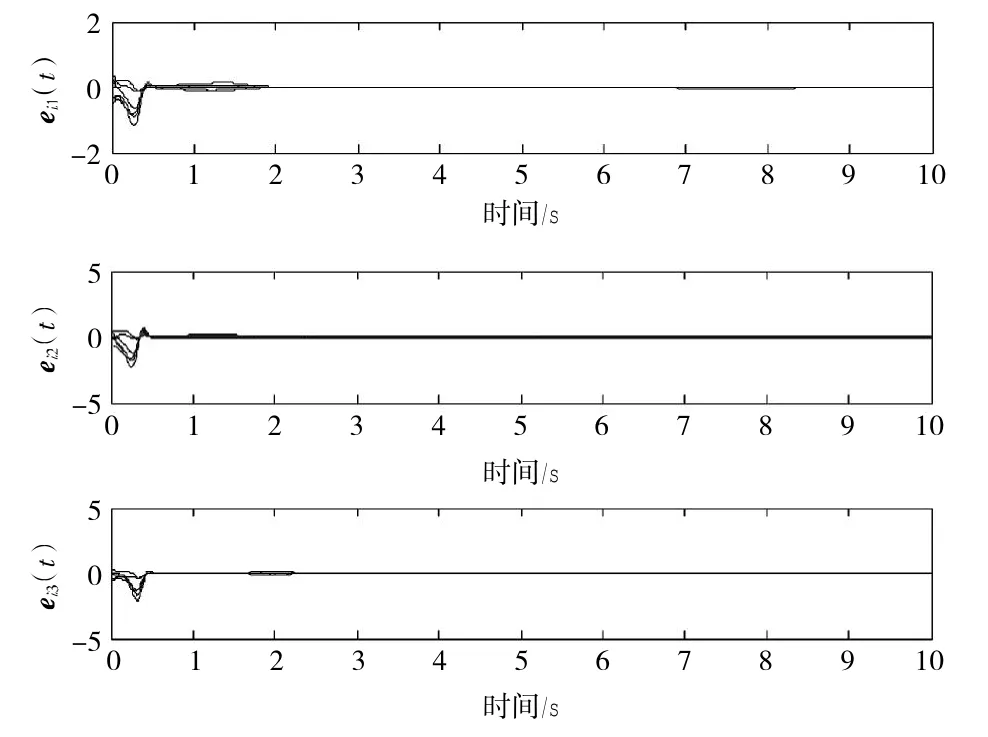
图1 在控制器（10）下的系统误差ei1（t），ei2（t）,ei3（t）Fig.1 Synchionization errors ei1（t）,ei2（t）,ei3（t）under updating law(10)

再来考虑两系统配置不同的情况，耦合矩阵取值为

其他参数与上一实验相同，根据推论1选择控制器（10）。

4 结语

讨论了耦合项和节点含有时变时延和非时延的复杂网络的同步问题。基于Lyapunov稳定性理论和线性矩阵不等式，给出了网络同步的充分条件，并给出两个推论。为了证实有效性，利用Matlab进行数值仿真。如图1、图2所示，网络误差曲线迅速收敛到0，说明网络达到了同步状态。数值仿真结果验证了方法的有效性。

Adaptive synchronization of complex networks with time-varying delays and non-delay coupling

GONG Chang-zhong，CAI Xiao-dong
（College of Science，CAUC，Tianjin 300300，China）

The adaptive synchronization between two complex networks with time-varying delays and non-delays coupling is studied，which does not require that the coupling matrix is symmetric or irreducible.Based on stability theory of Lyapunov，several criteria for synchronization of two complex networks are obtained，considering the case of network topological structures.Finally，the results of numerical simulations can prove the criteria.

complex network；synchronization；time-varying delay；non-delay；coupling

TP273

：A

：1674-5590（2014）06-0048-04

2013-07-12；

：2013-10-15

：中央高校基本科研业务费专项（ZXH2012B003，ZXH2012K002）

巩长忠（1959—），男，山东蓬莱人，教授，博士，研究方向为非线性控制.