一种舰艇水下爆炸冲击响应的简化分析方法

张晓君，杜志鹏，谢永和

（1.浙江海洋学院船舶与海洋工程学院，浙江舟山 316022；2.海军装备研究院，北京 100073）

一种舰艇水下爆炸冲击响应的简化分析方法

张晓君1，杜志鹏2，谢永和1

（1.浙江海洋学院船舶与海洋工程学院，浙江舟山 316022；2.海军装备研究院，北京 100073）

针对舰船设计初期缺少水下爆炸冲击响应预估方法的问题，提出了一种将DDAM方法和Taylor平板理论相结合的舰艇水下爆炸冲击响应理论模型。该理论模型根据Taylor平板理论将船底简化为自由平板，根据DDAM方法将船体结构各层甲板简化为质量-弹簧系统以模拟各层甲板对底舱的反作用。计算得到了船体结构各层甲板冲击响应，并与缩比模型试验数据进行了对比验证。结果表明这种简化分析方法能够较好模拟舰艇舱段各层甲板在水下爆炸的冲击响应，可为舰艇设计初期的冲击环境预估提供借鉴。

水下爆炸；舰艇冲击响应；简化分析方法；DDAM方法；Taylor平板理论

水下爆炸是海军舰艇面临的严重威胁，二战以后美军受严重损伤的水面舰艇中60%以上是水下爆炸所致[1]。水下爆炸不仅破坏水面舰艇船体结构，而且通过船体结构将冲击传递到舰载设备基础和舰员战位，从而引起大量设备失效和舰员受伤，使舰艇丧失战斗力和航行能力[2]。为对这种冲击危害进行有效防护，首先要弄清冲击在船体结构中的传播与衰减的规律，并掌握各种水下爆炸对不同水面舰艇各部位所造成的冲击量值。

GEERS[3]发展了双渐进法（DAA）用于处理水下爆炸与船体冲击响应之间的流固耦合问题。刘建湖[4]在DAA基础上发展了能够分析声学材料流固相互作用的ADAA方法(Acoustic DAA)。姚熊亮等[5]提出了一种在ANSYS/LS-DYNA中计算舰船水下非接触性爆炸冲击动响应的平断面加载法，模拟冲击波载荷，用于计算舰船冲击响应。

通过上述数值仿真技术的发展，可以较准确地得出水下爆炸作用下舰艇各部位冲击响应量值。然而，建模仿真必须在舰艇设计基本完成后，根据图纸建模仿真，也就是事后评估，难以对舰艇的设计方案提供直接的借鉴。在进行舰艇设计的一定阶段，需要根据所设计舰艇的吨位、主尺度及主要结构件尺寸等一系列初步参数，估算出水下爆炸作用下舰艇各层甲板冲击响应分布规律。为此需要发展一种简化的理论模型，既能考虑水下爆炸与船体的流固耦合效应，又能反映船体各层甲板之间的冲击传递与反作用，使新型舰艇设计时能够更好的根据冲击传递规律进行冲击防护。

在理论方法方面，舰艇水下爆炸这一动力学问题具有复杂的流固耦合过程，目前还只能对简单结构物得到解析解。TAYLOR[6]最先提出了一种刚性自由平板在水下爆炸作用下的流固耦合模型。该模型将船体外壳假设为无约束平板，当水中入射冲击波进行到平板时、在平板表面完全反射；与此同时平板开始运动、并由此产生出水中稀疏波；当水中总压力降为0时，平板也达到其峰值速度。REID[7]对比分析了Taylor平板理论预测峰值的速度结果与试验数据，发现其误差约在±20%。张文鹏等[8]拓展了Taylor平板理论，考虑横剖面运动的附加质量，建立二维横剖面在非接触水下爆炸冲击波作用下的运动方程。在此基础上计算某艇在水下爆炸冲击波作用下的刚体响应，与实验结果一致。但是整船的刚体运动响应还无法分解得到各层甲板的冲击响应。这是因为各层甲板以及舱壁之间存在复杂的支撑关系，由此产生了冲击作用下的冲击传递与反作用的复杂耦合关系。

对舰艇这种复杂结构冲击耦合作用的工程预测方法的最早研究，来自美国海军研究所NRL BELSHEIM和O′HARA。早在1961年，他们即提出了基于冲击谱的DDAM方法[9]。这种方法主要用于舰用设备内各零部件之间的冲击耦合作用预测。DDAM方法的基本思路是：首先，建立起设备系统的数学模型和振动方程，并求解其正则振型；其次，根据其基础冲击谱计算出每一正则振型的最大冲击响应，最后，把这些正则振型的最大响应予以叠加，即可以得到设备系统各零部件冲击响应的估算。但是DDAM方法无法考虑舰艇水下爆炸流固耦合作用。

本文针对舰船设计初期缺少水下爆炸冲击响应预估方法的问题，提出了一种将DDAM方法和Taylor平板理论相结合的舰艇水下爆炸冲击响应理论模型。该理论模型根据DDAM方法将船体结构各层甲板简化为质量-弹簧系统，根据Taylor平板理论将船底简化为自由平板，但其中包含了其他各层甲板的冲击反作用力。最终推导得出整个舰艇与水下爆炸载荷系统的控制方程。通过对该方程的数值求解，得到了船体结构各层甲板冲击响应，并与缩比模型试验数据进行了对比验证。

1 理论模型

建立舰艇舱段水下爆炸冲击响应理论模型，见图1所示。各层甲板用质量块模拟，甲板之间舱壁的刚度用弹簧刚度模拟。发生水下爆炸时，位于舰船水线以下部位的船体外壳（以下简称底舱），直接受到爆炸冲击波的作用，并进一步通过甲板、舱壁等结构将冲击传递至整个船体。与此同时，来自于其它部位船体和设备的惯性力也反作用于底舱。

图1 水下爆炸作用下的舰船冲击响应示意图Fig.1 Sketch map of warship shock response under the underwater explosion

以底舱质量块为研究对象，作用于其上的外力包括：水下爆炸冲击波总压力Fs、各层甲板作用于底舱的反作用惯性力Fg，底舱运动时产生的水阻力为Fz，则底舱动力学方程可以写为：

底舱湿表面受到的水中冲击波总压力为：

式中，A为底舱湿表面等效面积；PT为水中压力，在大于空穴压力PC（通常取0）时，水中压力等于入射与反射冲击波之和，当其小于空穴压力时，则恒等于空穴压力[6]，如下所示：

其中，ρ和c分别是水的密度和声速，通常取1 000 kg/m3和1 500 m/s；水下爆炸冲击波压力为PW=对于等效TNT当量为W（kg）的装药，冲击波峰值压力计算公式为[7]：

冲击波衰减常数计算公式为：

底舱受到的各层甲板和设备惯性力Fg为[2]：

式中，Mj为各层甲板和设备组成的系统第j阶模态质量；ωj为第j阶圆频率。

由于底舱湿表面运动而产生的水阻力Fz为[6]：

式中，cd为阻力系数，对于圆舭形船体该系数可取为0.75。

将Fs、Fg和Fz代入后整理得到：

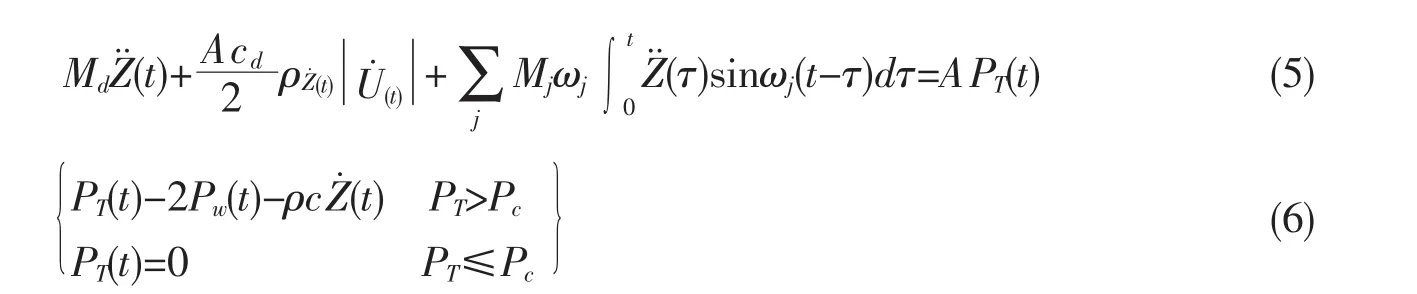
方程（5）就是在水下爆炸作用下考虑船体与水的流固耦合以及与各层甲板和设备相互作用的动力学模型。其中，方程左边第一项为船底板的惯性力，第二项为船底板表面流体粘性力，第三项为各层甲板和设备的惯性力，方程右边为水下爆炸冲击波压力载荷项。如果去掉第三项则变为Taylor平板理论。如果去掉第二项和等号右端项则成为无流体影响的弹性系统。方程（5）是一个关于Z的积分微分方程，需要对其进行数值积分求得数值解。

在求得底舱自由度动力响应Z后，舰艇一体化冲击响应问题就转变为已知基础激励Z¨(t)的多自由度动力学的常规问题【舰船现代冲击理论及应用】：

其中，[M]是各层甲板的集中质量，[K]和{x}分别是各层甲板的刚度矩阵及位移向量，{1}是单位向量。可以采用通常的模态叠加或直接积分法求解得到各层甲板在基础激励Z¨下的响应。

各层甲板之间的舱壁和舷侧板架是甲板的支撑，同时也是垂向冲击力的传递路径。将沿垂向自由度方向的舱壁和舷侧板架近似为剖面面积为A、长度为L的杆。其刚度为k=EA/L，其中E为舱壁和舷侧板架选用材料的杨氏模量。

2 算例与分析

取文献[10]中某舰船得缩尺比模型作为研究对象，利用本文方法计算分析其底舱、平台、甲板的冲击响应。分析模型物理参数主要包括：舱段总质量9.6 t，底舱质量5.2 t、平台层质量3.0 t、甲板质量1.4 t。

主要构件为：舱壁板，板厚2 mm；扶强材平台至甲板，T型材规格1×24/1.2×12；平台至底舱，角钢规格12×5；T材及角钢间距均为0.1 m。外板板厚3 mm，肋骨间距0.3 m。支柱尺寸Φ25×1.4，支柱距中1.4 m。根据这些参数利用k=EA/L的公式，可估算出平台与甲板间的刚度为3.6×109N/m，平台与底舱间的刚度为1.86×109N/m。据此给出由3个集中质量和2个线性弹簧组成的舰船舱段垂向冲击响应计算模型。

舰船缩比模型的水下爆炸工况为5 kg TNT当量爆源，舷侧7.61 m水深6 m。实测水下爆炸自由场冲击波压力峰值7.1 MPa，壁压12 MPa。按照式（6）计算得到的压力时域曲线如图2所示，与实测峰值吻合。从壁压曲线特征可以看出，在初始冲击波峰值过后，压力迅速降为0。这是由于底舱在冲击波作用下产生垂向速度Z˙，使得式（6）的PT小于0，引起水中空化。此后直到底舱速度逐渐降低，总压力PT恢复到0以上，使冲击波压力再次作用于底舱，如此反复形成后续多次冲击压力。

图2 底舱壁压计算结果Fig.2 Calculation result of bulkhead pressure in bottom tank

图3 底舱、平台和甲板冲击加速度响应计算结果Fig.3 Calculation result of the shock acceleration for bottom tank,platform and deck

计算得到底舱、平台和甲板的等效质量在冲击下的加速度响应，如图3。从图3可以看出，底舱质量在初始冲击波作用下产生了峰值达1 500 m/s2的加速度响应，随后迅速降低至约240 m/s2。在经过底舱与平台之间舱壁的衰减后，代表平台的质量冲击加速度峰值降为约450 m/s2，并在结构阻尼作用下进一步衰减。另外，平台的冲击响应还受到其上的甲板反作用。平台的冲击运动通过平台与甲板间舱壁传递到甲板层面，由于甲板不受冲击反作用力，因此其首个周期冲击加速度峰值与平台接近，而后续周期比平台还要高。

为了验证本文理论模型，将计算结果与试验数据进行对比。图4（a）和图4（b）分别是平台质量的实测和计算加速度曲线。试验数据的峰值比计算结果高，但这些峰值是高频分量，对舰艇结构的实际加速度作用并不明显。

将试验实测加速度数据积分得到平台层面速度和位移时域曲线，与计算结果进行对比，如图5、图6所示。显然，在对试验和计算得到的平台加速度进行一次时间积分得到平台速度时域曲线后，两者的峰值和趋势就基本一致了。两次时间积分得到位移曲线更为吻合，说明用本文给出的3质量模型能够较好地模拟舱段水下爆炸冲击响应。

图5 平台速度的试验数据与计算值对比Fig.5 Velocity comparison of platform

图6 平台位移的试验数据与计算值对比Fig.6 Displacement comparison of platform

3 结论

本文所提出的一种将DDAM方法和Taylor平板理论相结合的舰艇水下爆炸冲击响应理论模型根据Taylor平板理论将船底简化为自由平板，根据DDAM方法将船体结构各层甲板简化为质量-弹簧系统、模拟各层甲板对底舱的反作用。将本文方法的计算结果与试验数据对比分析，得到结论如下：

（1）本文提出的舰船多层甲板冲击响应简化分析模型物理意义明确，计算分析结果可信；

（2）利用本文方法计算获取的加速度冲击响应数据所蕴含的能量与实测数据差别较小，满足工程应用要求；

（3）由于将舰艇结构和设备用集中质量模拟，掩盖了冲击响应高频分量，但并不影响总体冲击响应的预估。

[1]WEBSTER K G.Investigation of Close Proximity Underwater Explosion Effects on a Ship-Like Structure Using the Multi-Material Arbitrary Lagrangian-Eulerian Finite Element Method[R].Faculty of Virginia Polytechnic Institute and State University，2007.

[2]汪 玉,华宏星.舰船现代冲击理论及应用[M].北京:科学出版社,2005.

[3]GEERS T L.Doubly asymptotic approximations for transient motions of submerged structures[J].The Journal of the Acoustical Society of America,1978,64:1 500-1 508.

[4]刘建湖.舰船非接触水下爆炸动力学的理论与应用[D].无锡:中国船舶科学研究中心,2002.

[5]姚熊亮,郭 君,许维军.船舶结构远场爆炸冲击动响应的数值试验方法[J].中国造船,2006,47(2):24-34.

[6]TAYLOR G I.The pressure and impulse of submarine explosion waves on plates[M].The Scientific Papers of G.I.Taylor,Vol. III.Cambridge University Press.1963.

[7]REID W D.The response of surface ships to underwater explosions[R].DSTO-GD-0109.1996.

[8]张文鹏,宗 智,汪 玉,杜志鹏.冲击波作用下舰船刚体运动响应[J].噪声与振动控制,2012,32(6):134-136.

[9]BELSHEIM R O,O'HARA G J.Shock design of shipboard equipment,dynamic design analysis method[R].NAVSEA Report 250-423-30,1961.

[10]汪 玉.舰艇水下爆炸试验及冲击分析技术[M].北京:国防工业出版社,2008.

A Simplified Method for Analysis Underwater Shock Response of Warship

ZHANG Xiao-jun1,DU Zhi-peng2,XIE Yong-he1
（1.Naval Architecture and Ocean Engineering School of Zhejiang Ocean University,Zhoushan 316022; 2.Naval Academy of Armament,Beijing 100073,China）

According to the lack of methods of predicting underwater shock response at the early design stage,this article present a theoretical model of underwater impact response,which combines the DDAM method and Taylor plate theory.In the theoretical model,ship bottom can be simplified as a free plate according to Taylor plate theory,and the decks of the ship can be simplified as Mass-spring System to simulate the reaction of the decks to the bottom.The impact response to each deck is calculated,and its validation is conformed in contrast to the results of shrink ratio experiments.Therefore,the simplified analysis method can simulate each deck's impact response due to underwater explosion,and can provide references for the prediction of shock environment at the early design stage of warship.

underwater explosion;warship impact response;simplified analysis method;DDAM method; Taylor plate theory

O383+.1；U663.85

A

1008－830X(2014)04－0293－05

2014-03-11

张晓君（1972-），女，北京市人，副教授，研究方向：船舶与海洋工程结构物设计建造.