Generation of Nonlinear Evolution Equations by Reductions of the Self-Dual Yang–Mills Equations∗

ZHANG Yu-Feng(张玉峰)and Hon-Wah Tam

1 Introduction

We have known the fact that the Lax-pair method is an important approach for generating integrable systems.The compatibility condition of the simplest Lax pair

where U,V,and φ belong to a scalar Lie algebra,is equivalent to the standard zero curvature equation

By using such the Lax pair(1)and Eq.(2),some inf inite dimensional integrable hierarchies of evolution equations were obtained.For example,Tu[1−2]once obtained the AKNS hierarchy,KN hierarchy via introducing appropriate Lie algebras under the frame of the Lax pair(1).Furthermore,Tu[1]once again created a powerful tool for deducing Hamiltonian structures of integrable hierarchies derived,called the trace identity. The approach presented in Ref.[1]is called the Tu scheme by Ma.Making use of the Tu scheme,some interesting integrable hierarchies including their some algebraic and geometric properties were available.[3−12]Specially,in Ref.[12]two kinds of higher-dimensional Lie algebras were introduced for which the integrable couplings of the BK and DLW hierarchies were obtained.By using the Lax pair(1)some f i nite-dimensional integrable hierarchies and the associated properties can also be obtained.For example,Cao[13−14]proposed the non-linearization method to transform inf i nite-dimensional integrable systems to f i nite-dimensional ones under the frame of the Lax pair(1)and the Lenord series.Following the approach some f i nite-dimensional integrable systems and their Hamiltonian structures,algebraic-geometric solutions are produced.[13−17]

The Lax pair(1)is actually a special case of the Lax pair,which corresponds to the sdYM equations.In fact,the sdYM equations are equations for a connection A on a vector bundle E related to the principal bundle over a complex four-manifold M with a Lie group G acting on the f i bers.Introducing the curvature form F of the connection A and the Hodge star-operator∗,the sdYM equations can be written as:[18−19]

In terms of local coordinates xaon M,the connection A and the curvature F can be written as

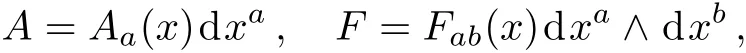
where Fab= ∂aAb−∂bAa−[Aa,Ab],and the Aa,Abbelong to the Lie algebra g,which is isomorphic to the fi bers of the vector bundle over M.Aaand Fabare referred to the Yang–Mills connection or potential and the Yang–Mills fi eld,respectively.If we introduce on M the complex coordinates(ω,ω¯,z,z¯)and the metric ds2=dωdω¯+dzdz¯,then(3)can be written as:[18−19]

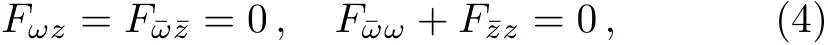
which are the integrable conditions for the following Lax pair here D1=∂ω+λ∂¯z,A1=Aω+λA¯z,D2=∂z−λ∂¯ω,A2=Az−λA¯ω.

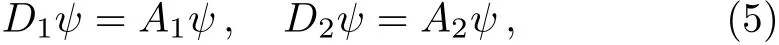
The compatibility condition of Eq.(5)presents that

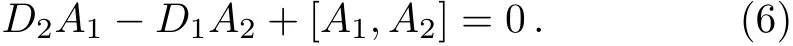
When taking λ=0,Eq.(5)reduces to Eq.(1)and Eq.(6)does to Eq.(2).In Ref.[18]an important fact has been proved that in a suitable gauge the components A¯ωand A¯zcan be represented by two commuting elements in g.Therefore,we have the reasion to choose the gauge for the following equation to hold:

Following the ideas in Refs.[8,19],we shall reduce the Lax pair,i.e.the linear problem(5),to a simpler form by imposing the space-time symmetry.Then making use of the compatibility condition(6)and a spectral-function transformation yields a set of(2+1)-dimensional equations,which are our deducing starting point.The f i rst reduction produces a generalized Burgers equation with a variablecoeきcient function,which further reduces to the forced Burgers equation,the heat equation,the Fisher equation,and the Huxley equation,respectively.The second reduction yields a(2+1)-dimensional integrable system,which can be reduced to(2+1)-dimensional integrable couplings of a(2+1)-dimensional nonlinear integrable equation obtained in the paper.The paper shows us a way for generating(2+1)-dimensional integrable systems,specially an approach for producing(2+1)-dimensional integrable couplings.

2 A Reduction of the sdYM Equations

We introduce a ring of diあerential operators with an auxiliary variable y as follows

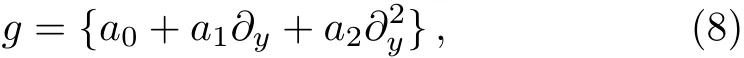
where aibelong to a ring of n×n complex-matrix functions of y,x and t,∂y= ∂/∂y.Assume the Yang–Mills potentials are independent of the variable ω+ω¯ and z.We redefi ne the remaining coordinates asz¯−z≡x,ω ≡t,the component of the connection presents the form Aa=Aa(x,t).It is easy to see that D1= ∂t+λ∂x,D2= −∂x.Thus,the linear problem(5)reduces to the following simpler form:

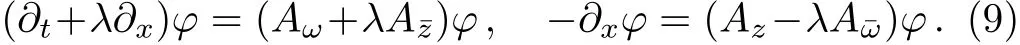
Substituting the second equation in Eq.(9)into the f i rst one yields

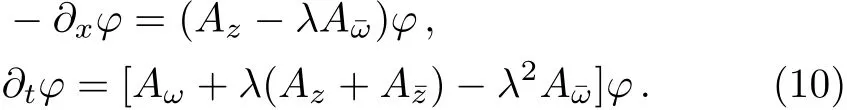
Now we choose the appropriate components of the connection in terms of the ring of the diあerential operators as follows

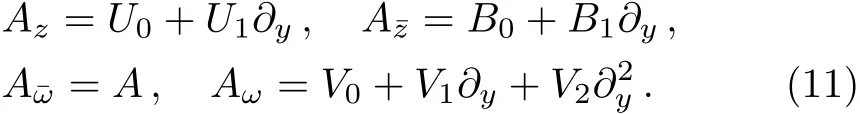
Thus,the gauge condition(7)becomes

0 In what follows,we want to simplify the linear problem(10).Assume ϕ =2φ sinh(λy),and substituting Eqs.(11)and(12)into Eq.(10),we get two sets of equations

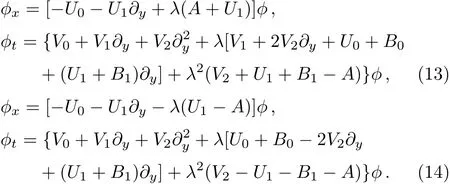
3 A Variable-Coeきcient Burgers Equation and a New(2+1)-Dimensional Integrable Coupling

In what follows,we start from the reduced linear problem(13)to deduce(1+1)-dimensional and(2+1)-dimensional integrable equations,specially obtain a(2+1)-dimensional integrable coupling of a new(2+1)-dimensional integrable nonlinear equation.In order to eliminate λ in Eq.(13),we set U1= −V2=A,V1=−U0−B0,B1=3A.Hence,Eq.(13)reduces to the following form:

The compatibility condition of Eq.(15)gives rise to the following equations

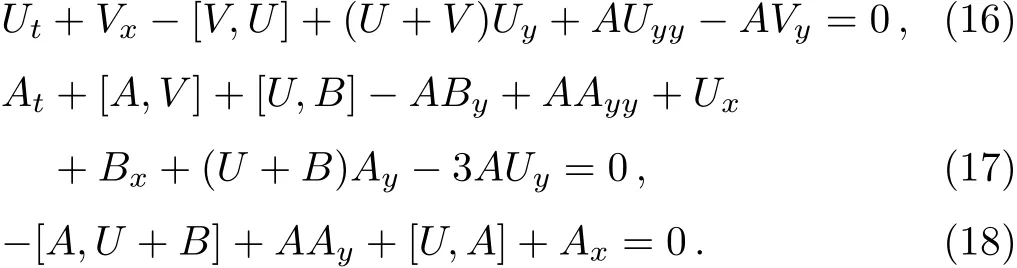
By using Eq.(12),Eq.(18)reduces to again

3.1 The Case where A,B,U,V in Eq.(15)are Scalar Functions

Take A=1,then Eqs.(16)and(17)reduce to

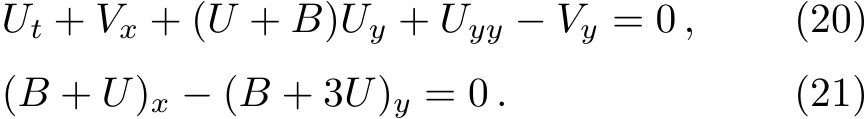
Set

where α(t)is an arbitrary derivative function in t,g=g(x,y,t)is an arbitrary derivative function,then Eq.(21)holds.While Eq.(20)becomes that

Let us change the coordinates,X=x−y,Y=y.Then Eq.(22)casts into

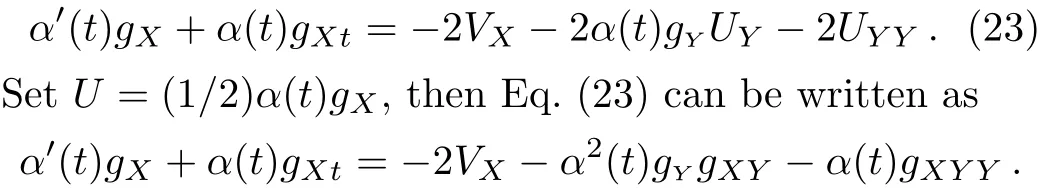
This equation can be integrated once and we have

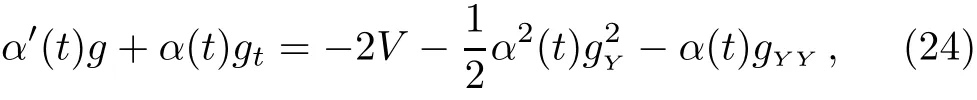
which is a generalized Burgers equation with the variablecoeきcient α(t)and the forced term −2V.If set α(t)=1,then Eq.(24)becomes that

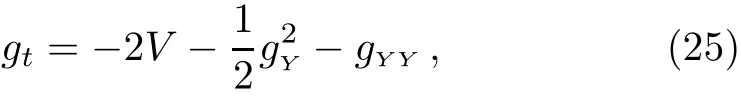
which is the forced Burgers equation presented in Ref.[19].

If set V=−(1/4)g2Y,then Eq.(25)reduces to the heat equation

If set V=0,and diあerentiate(25)with respect to Y,we get

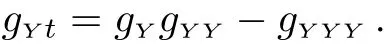
Let gY=u,we have the standard Burgers equation

The obtained equations as above are consistent to ones in Ref.[19].

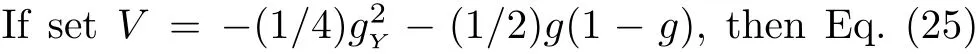
reduces to the Fisher equation

Assume again V = −(1/4)g2Y−(1/2)g2(1−g),then Eq.(25)reduces to the Huxley equation

3.2 The Case where A,B,U,V are 3×3 Matrices

We f i rst present the gauge transformation of Eq.(15).Setˆφ=h(x,y,t)φ and substitute it into the following equation

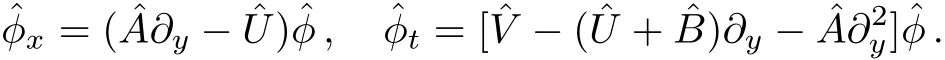
After calculation we have that

In order to preserve A,we take

Due to requiring[A,B]=0,we can take

where b1and b2are to be determined.To keep the form of U invariant,we set

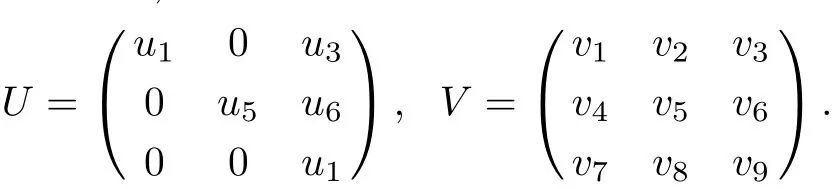
Then Eq.(19)obviousely holds.Substituting A,B,U,V as above into Eq.(17)leads to the following equations

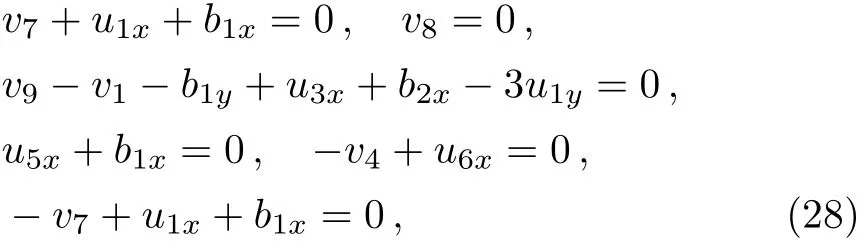
which give that

where we take the integration constants to be zero.Inserting A,B,U,V into Eq.(16),we have

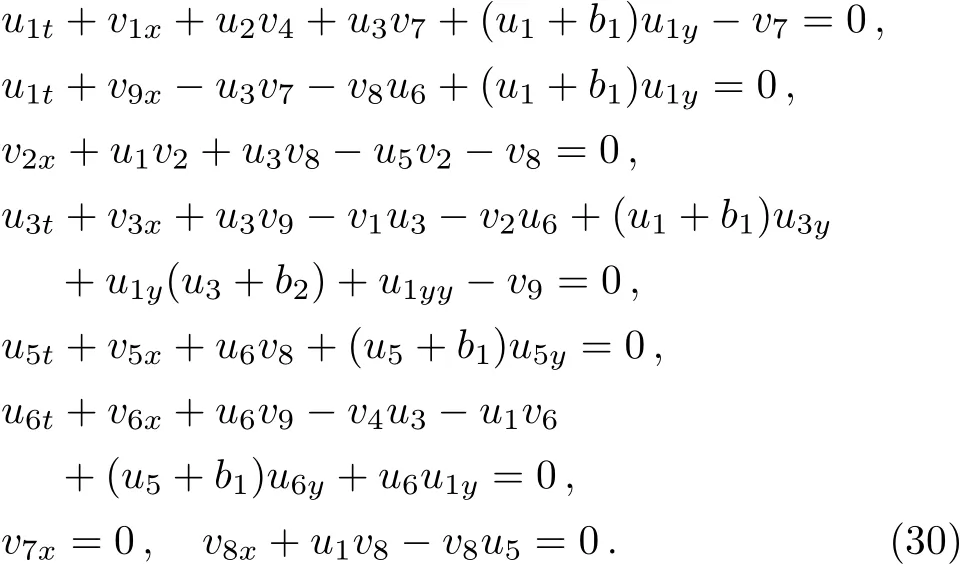
Set v1=v9,Eqs.(28)and(30)give rise to the following:

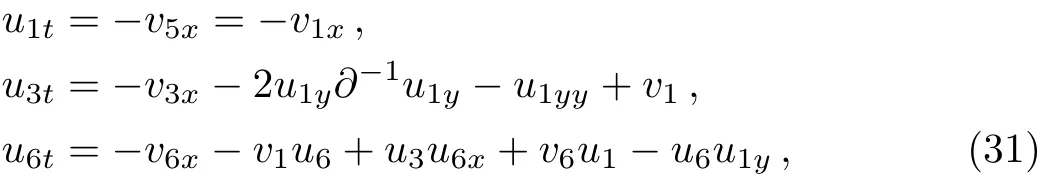
which is a(2+1)-dimensional coupled equation.In what follows,we consider its reductions.

Case 1 Set u3=u6=v3=v6=0,Eq.(31)reduces to a new(2+1)-dimensional integrable equation

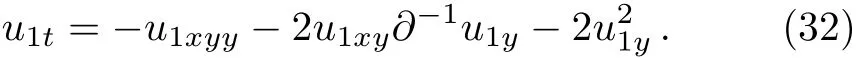
Case 2 Set u3=v3=0.We have v1=u1yy+2u1y∂−1u1y,Eq.(31)reduces to the(2+1)-dimensional integrable system

In terms of theory on integrable couplings,[20−21]the above system(33)is a(2+1)-dimensional integrable coupling with the forced term−v6x.

[1]G.Z.Tu,J.Math.Phys.30(1989)330.

[2]G.Z.Tu,J.Phys.A 22(1989)2375.

[3]W.X.Ma,Chin.J.Contemp Math.13(1992)79.

[4]W.X.Ma,J.Phys.A 25(1992)L719.

[5]X.B.Hu,J.Phys.A 27(1994)2497.

[6]X.B.Hu,J.Phys.A 30(1997)619.

[7]E.G.Fan,J.Phys.A 42(2009)1751.

[8]E.G.Fan,J.Math.Phys.50(2009)013525.

[9]Y.F.Zhang and H.Q.Zhang,J.Math.Phys.43(2002)466.

[10]Y.F.Zhang and J.Q.Mei,Commun.Theor.Phys.52(2012)1012.

[11]Y.F.Zhang and J.Liu,Commun.Theor.Phys.50(2008)593.

[12]Y.F.Zhang,Commun.Theor.Phys.55(2011)273.

[13]C.W.Cao,Science in China 33(1990)528.

[14]C.W.Cao,Acta Mathematica Sinica,New Series 7(1991)216.

[15]C.W.Cao,X.G.Geng,and H.Y.Wang,J.Math.Phys.43(2002)621.

[16]X.G.Geng and H.H.Dai,J.Math.Phys.41(2000)337.

[17]C.W.Cao and B.Q.Xia,Commun.Theor.Phys.53(2010)619.

[18]M.J.Ablowitz,S.Chakravarty,and L.A.Takhtajan,Commun.Math.Phys.158(1993)289.

[19]S.Chakeavarty,S.L.Kent,and E.T.Newman,J.Math.Phys.36(1995)763.

[20]B.Fuchssteiner,Coupling of Completely Integrable System:the Perturbation Bundle,ed.P.A.Clarkson,Applications of Analytic and Geometric Methods to Nonlinear Diあerential Equations,Kluwer,Dordrecht(1993)p.125.

[21]W.X.Ma,Method and Applications of Analysis 7(2000)21.