Propagation of Lorentz–Gaussian Beams in Strongly Nonlocal Nonlinear Media
2014-03-12KeshavarzandHonarasa
A.Keshavarz and G.Honarasa
Department of Physics,Faculty of Science,Shiraz University of Technology,Shiraz,Iran
1 Introduction
The Lorentz–Gaussian beam,as a more generalized case of Lorentz beam,has been introduced by Gawhary and Severini.[1]The Lorentz–Gaussian beam can describe the radiation emitted by single-mode diode lasers.[2−3]The beam propagation factors and nonparaxial propagation of a Lorentz–Gaussian beam have been investigated.[4−6]The Wigner distribution function of Lorentz–Gauss beams through a paraxial ABCD optical system has also been derived by Zhou and Chen.[7]The propagation of Lorentz–Gauss beams through a few optical systems and diあerent media such as turbulent atmosphere and uniaxial crystals have been investigated.[8−11]
In nonlocal nonlinear media(NNM),the refractive index at a particular point depends on the beam intensity at all other material points.[12]When the beam width is much shorter than the width of the material response function,the media are called strongly nonlocal nonlinear media(SNNM).[13]This property is observed in several optical materials such as lead glasses[14]and nematic liquid crystals.[15−16]The propagation of various optical beams such as Hermite–Gaussian,Laguerre–Gaussian,Hermite–Laguerre–Gaussian,Ince–Gaussian and four-petal Gaussian beams in nonlocal nonlinear media have been studied.[17−21]
According to our knowledge,the propagation of Lorentz–Gaussian beams in SNNM has not been reported elsewhere.In this paper,the evolutions of intensity distribution,the beam width and the curvature radius of a Lorentz–Gaussian beam during propagation in SNNM are studied based on Collins formula and ABCD method.
The paper is organized as follows:In Sec.2,the theory of our formalism is exposed to study the propagation of Lorentz–Gaussian beams in SNNM.Propagation properties of Lorentz–Gaussian beams during the propagation in SNNM are investigated in Sec.3.Conclusion of the paper is also presented in Sec.4.
2 Theory
The Lorentz–Gaussian beam in the Cartesian coordinates at z=0 plane is introduced as:[1]

with

where j=x or y,ω0jis the parameter related to the beam width of Lorentz part in j-direction and ω0is the waist of the Gaussian part.The Lorentz distribution can be expressed in terms of Hermite–Gaussian functions:[22]

where N is the number of terms in the expansion and σ2mis given by
“民国三十一年,农历四月二十三日午时,吉日吉时,孔家孔守真、子孔志新出殡奠礼现在开始,第一项:盖棺。”

where erfc(·)and H2m(·)are the complementary error function and the 2m-th order Hermite polynomial,respectively.With the help of Eq.(4),E(j,0)can be obtained as follows
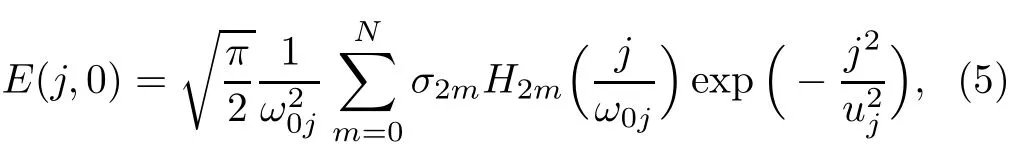
where

Propagation of the optical beams through an optical system,which is parameterized by an ABCD transfer matrix can be described by the generalized Collins formula:[23]

where E(j0,0)is the f i eld distribution at entrance plane z=0,λ is the wavelength of the beam and k is the wave number.Here A,B,and D are the elements of the transfer ABCD matrix.By using the integral formula

the following analytical expression for propagation of Lorentz–Gaussian beams through an optical ABCD system can be derived as:

where αjis def i ned by
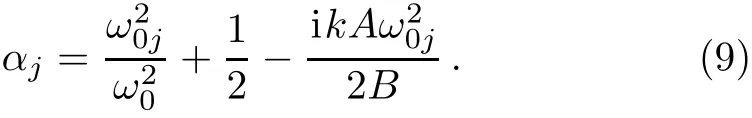
The propagation of beams in nonlocal nonlinear media is governed by the nonlocal nonlinear Schr¨odinger equation

where
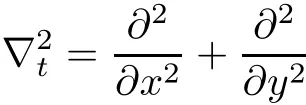
is the transverse Laplacian operator,k is the wave number in the media without nonlinearity,n0is the linear refractive index of the media,

is the nonlinear perturbation of refractive index,n2is the nonlinear index coeきcient and R is the normalized symmetrical real spatial response function of the media.
In the case of strong nonlocality,by the use of Snyder and Mitchell model,Eq.(10)takes the form[24−25]
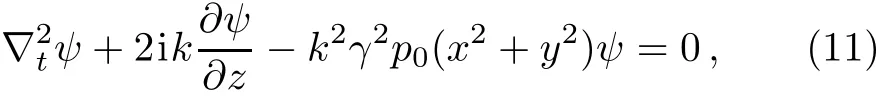
where γ is the material constant relating to the response function and p0is the input power at z=0.As ABCD matrix is widely used to describe the beam propagation through the paraxial optical systems and the beam propagation equation in SNNM can be linearized,it is straight forward to show that the beam propagation in SNNM can be described by following ABCD matrix[12]

where z0= πω20/2 is Rayleigh distance,pc=(z20γ2)−1is the critical power of Gaussian beam and p0is the input power.
By inserting the elements of transfer matrix(12)in Eq.(8)the analytical expressions for propagation of Lorentz–Gaussian beams in SNNM can be written in the form

Figure 1 shows the transverse f i eld distribution of a typical Lorentz–Gaussian beam with ω0=3,ω0x=2,and ω0y=6 during propagation through the SNNM for different values of input powers.In Fig.2,the behavior of a Lorentz–Gaussian beam is simulated in x–z and y–z plane.These analytical simulations are based on Eq.(13).The results show that when the Lorentz–Gaussianbeam propagates through SNNM,the intensity distribution varies periodically.The period distance is z=which can be found from Eq.(12).Therefore,the evaluation period with a smaller input power is longer than that with a larger input power.

Fig.1 Transverse f i eld distribution of a Lorentz–Gaussian beam with ω0=3, ω0x=2,and ω0y=6 through the SNNM at diあerent propagation distances:z/z0=0(f i rst column),z/z0=2(second column),z/z0=4(third column),and z/z0=6(fourth column).The diあerent rows represent various values of the input powers:p0/pc=0.7(f i rst row),p0/pc=1.0(second row),and p0/pc=1.3(third row).
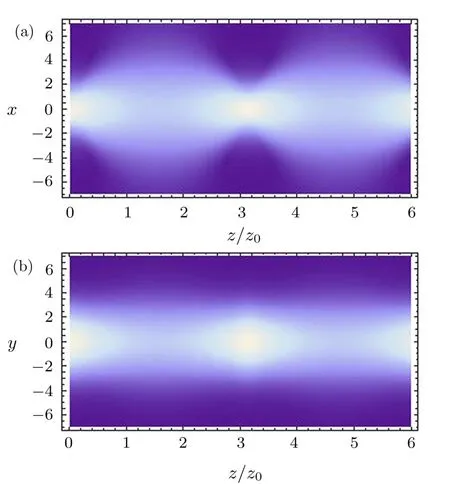
Fig.2 Transverse distribution of a Lorentz–Gaussian beam with ω0=3, ω0x=2,and ω0y=6 through the SNNM in x-z and y-z planes for p0=pc.
3 Propagation Properties of Lorentz–Gaus–sian Beams
In this section,the evolution of the beam width and the mean curvature of Lorentz–Gaussian beams in SNNM based on ABCD matrix are investigated.
The second-order moment of the intensity certainly gives good eminent information on the beam width.The second-order moment beam width at the waist plane w1can be expressed as[26]

and the beam width at the observation plane w2after propagation through an optical ABDC system is related to w1as follows

with

where φ(x,y)and ψ(x,y)are the phase and the amplitude of the beam,respectively.At the waist plane φ(x,y)=0 and so V1=0.The radius of curvature for a general beam at observation plane is given by

Figure 3 displays the evolution of the beam width and the curvature radius of the Lorentz–Gaussian beam during propagation through the SNNM.For simplicity,only the beam width in x-direction is plotted.It can be found from Fig.3(a)that the beam width varies periodically and its period is shorter in larger input powers.Figure 3(b)shows that the curvature radius is inf i nite at entrance plane and it varies periodically during propagation.The positive(negative)curvature radius represents the cophasal surface is concave(convex)and induces the focusing(defocusing)of the beam.

Fig.3 The beam width and the curvature radius of a Lorentz–Gaussian beam in x-direction with ω0=3 and ω0x=2 through the SNNM for p0/pc=0.7(solid line),p0/pc=1.0(dashed line),and p0/pc=1.3(dot-dashed line).

Fig.4 Transverse distribution of a Lorentz–Gaussian beam with ω0=3, ω0x=2,and ω0y=6 through the SNNM in x-z and y-z planes for(a)p0=pLGcxand(b)p0=pLGcy.

Fig.5 The beam width and the curvature radius of a Lorentz–Gaussian beam in x-direction with ω0=3 and ω0x=2 through the SNNM for p0/pLGcx=0.7(solid line),p0/pLGcx=1.0(dashed line),and p0/pLGcx=1.3(dot-dashed line).
By inserting A and B from Eq.(12)into Eq.(15),we can obtain the critical power of the Lorentz–Gaussian beam in j-direction as follows

When the input power is equal to Eq.(18),the beam width of the Lorentz–Gaussian beam in j-direction keeps invariant during propagation through the SNNM.In general case,when ω0x/= ω0y,the value of the critical power of the Lorentz–Gaussian beam is diあerent for x and y-direction.In Fig.4,the propagation of a Lorentz–Gaussian beam through SNNM is simulated in x–z and y-z plane for(a)p0=pLcxGand(b)p0=pLcyG.The evolution of the beam width and the curvature radius of the Lorentz–Gaussian beam in x-direction during propagation through the SNNM are plotted in Fig.5 for diあerent value of input powers.It is seen that when p0=pLcxGthe beam width of the Lorentz–Gaussian beam is constant during propagation.Otherwise the beam width oscillates periodically along the propagation length.
4 Conclusion
In conclusion,a closed-form expression for propagation of the Lorentz–Gaussian beams through the SNNM has been derived by using Collins formula,and then based on it the propagation of these beams in SNNM is simulated.The results show that the intensity distribution and beam width of the Lorentz–Gaussian beam vary periodically during propagation.This is due to the propagation nature of the beam,which is in competition with nonlinearity of the medium.
[1]O.E.Gawhary and S.Severini,J.Opt.A,Pure Appl.Opt.8(2006)409.
[2]A.Naqwi and F.Durst,Appl.Opt.29(1990)1780.
[3]J.Yang,T.Chen,G.Ding,and X.Yuan,Proc.SPIE 6824(2008)68240A.
[4]G.Zhou,Appl.Phys.B 96(2009)149.
[5]G.Zhou,J.Opt.Soc.Am.B 26(2009)141.
[6]H.Yu,et al.,Optik 121(2010)1455.
[7]G.Zhou and R.Chen,Appl.Phys.B 107(2012)183.
[8]G.Zhou,J.Opt.Soc.Am.A 25(2008)2594.
[9]W.Du,C.Zhao,and Y.Cai,Opt.Lasers Eng.49(2011)25.
[10]G.Zhou and X.Chu,Opt.Express 18(2010)726.
[11]C.Zhao and Y.Cai,J.Mod.Opt.57(2010)375.
[12]Z.Yang,D.Lu,W.Hu,Y.Zheng,X.Gao,and Q.Guo,Phys.Lett.A 374(2010)4007.
[13]W.Krolikowski,O.Bang,J.J.Rasmussen,and J.Wyller,Phys.Rev.E 64(2001)016612.
[14]C.Rotschild,O.Cohen,O,Manela,M.Segev,and T.Carmon,Phys.Rev.Lett.95(2005)213904;C.Rotschild,M.Segev,Z.Xu,Y.V.Kartashov,L.Torner,and O.Cohen,Opt.Lett.31(2006)3312.
[15]M.Peccianti,K.A.Brzdakiewicz,and G.Assanto,Opt.Lett.27(2002)1460.
[16]C.Conti,M.Peccianti,and G.Assanto,Phys.Rev.Lett.92(2004)113902.
[17]D.Deng,X.Zhao,Q.Guo,and S.Lan,J.Opt.Soc.Am.B 24(2007)2537.
[18]D.Deng and Q.Guo,J.Opt.A:Pure Appl.Opt.10(2008)035101.
[19]D.Deng,Q.Guo,and W.Hu,J.Phys.B:At.Mol.Opt.Phys.41(2008)225402.
[20]D.Deng and Q.Guo,J.Phys.B:At.Mol.Opt.Phys.41(2008)145401.
[21]Z.Yang,D.Lu,D.Deng,S.Li,W.Hu,and Q.Guo,Opt.Commun.283(2010)595.
[22]P.P.Schmidt,J.Phys.B,At.Mol.Phys.9(1976)2331.
[23]S.A.Collins,J.Opt.Soc.Am.60(1970)1168.
[24]A.W.Snyder and D.J.Mitchell,Science 276(1997)1538.
[25]Q.Guo,B.Luo,F.H.Yi,S.Chi,and Y.Q.Xie,Phys.Rev.E 69(2004)016602.
[26]P.A.Belanger,Opt.Lett.16(1991)196.
猜你喜欢
杂志排行
Communications in Theoretical Physics的其它文章
- Exact Harmonic Metric for a Uniformly Moving Schwarzschild Black Hole∗
- Analytical and Numerical Studies of Quantum Plateau State in One Alternating Heisenberg Chain∗
- Dynamical Properties of a Diluted Dipolar-Interaction Heisenberg Spin Glass∗
- Conduction Band-Edge Non-Parabolicity Eあects on Impurity States in(In,Ga)N/GaN Cylindrical QWWs
- Electromagnetically Induced Transparency of Two Intense Circularly-Polarized Lasers in Cold Plasma:Beat-Wave Second Harmonic Eあect
- Stark-Chirped Rapid Adiabatic Passage in Presence of Dissipation for Quantum Computation∗
