Conduction Band-Edge Non-Parabolicity Eあects on Impurity States in(In,Ga)N/GaN Cylindrical QWWs

Haddou El Ghaziand Anouar Jorio

1LPS,Faculty of Science,Dhar EL Mehrez,BP 1796 Fes-Atlas,Morocco

2Special Mathematics,CPGE My Youssef,Rabat,Morocco

1 Introduction

Over the last decade,low-dimensional system(LDS)based on semiconductor materials such as quantum well(QW),quantum well wire(QWW),quantum dot(QD)and quantum ring(QR)form a major domain of research both theoretically and experimentally due to their potential applications especially in microelectronic devices technology.The conf i nement phenomena of particles(electron,hole)due to the size-reduction induces a dramatic change in their physical properties.It is well known that the presence of impurities in LDS plays an elementary role in some physical properties like optical,electrical and transport phenomena especially at low temperature.The main objective of addition of impurities in semiconductor heterostructures lies in altering the performance of quantum devices.Based on Ref.[1],several theoretical and experimental works concerning electrical and optical properties of shallow-donor in diあerent shapes of nanoparticles have been reported.[2−16]It is interesting to mention that all of works mentioned above have done within parabolic band approximation.For the more realistic description which takes into account of the energy dispersion relation,the LDS physical properties cannot be studied without considering the lift of the conduction band-edge.Recently,using the matrix diagonalization method,Rezaei et al.[17]have investigated the simultaneous eあects of conduction band non-parabolicity and hydrostatic pressure on binding energies of the ground-state and a few excitedstates in typical GaAs/(Al,Ga)As spherical QD.Panda et al.[18]have reported the eあects of conduction bandedge non-parabolicity on the linear and nonlinear optical properties in the Al0.3Ga0.7As/GaAs heterostructurebased symmetric rectangular QW under applied hydrostatic pressure and electric f i eld.Additionally,Revathi et al.[19]have calculated the donor binding energy of hydrogenic impurity in zinc blende GaN/AlxGa1−xNQD.The calculation has been carried out taking into account of conduction band-edge non-parabolicity eあect using the Luttinger-Kohn model.To the best of our knowledge,no work has been done to treat the conduction bandedge non-parabolicity on the hydrogenic impurity states in(In,Ga)N/GaN LDS.

In the present paper,we have performed the calculation of hydrogenic shallow-donor impurity ground-state binding energy as a function of ZB InxGa1−xN/GaN QWWs radius.The inf l uence of the conduction band-edge non-parabolicity is also investigated.Numerical calculations have been performed using the single band eあectivemass approximation using the Ritz-traditional variational procedure assuming the impurity is located on the wireaxis.

2 Theory

In this section,we restrict ourselves to a very brief presentation of two models adopted in this paper for studying the ground-state binding energy in ZB InxGa1−xN/GaN cylindrical QWWs under the conduction band-edge nonparabolicty(NP)eあect.We consider hydrogenic shallowdonor impurity located at the z-axis of the CQWW.Two Hamiltonian models of electron in circular-cross section wire of radius R,lying along z-axis are expressed as follow:

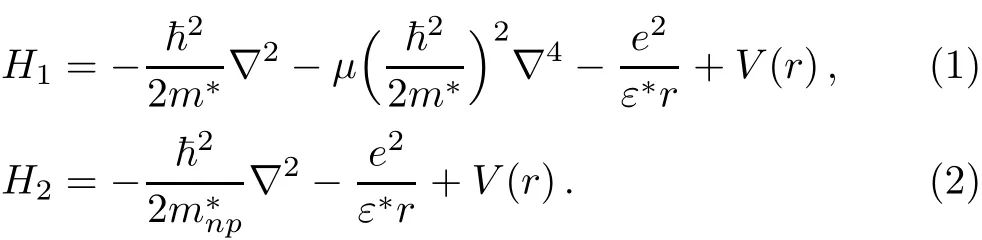
In Eqs.(1)and(2),m∗is the electron eあective-mass,ε∗is the dielectric constant,and e is the electron charge.The eあect of NP is included in our work through the parameterµ for the f i rst model and an energy-dependent eあectivemass m∗np=m∗γ(E)for the second model.According to Chaudhuri et al.,[20]this latter is given as:

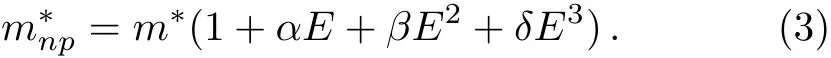
In Eq.(3),E is the electron energy while α, β,and δ are the parameters,which take into account of the eあective-mass dependence of the energy.In this work,we restrict our calculation to the f i rst order as used in Ref.[21].

The conduction band-edge NP factor is expressed as follows:[22]

In Eq.(4),y=Δ/Eg.Δ is the spin-orbit splitting energy while m0and Egare respectively the free-electron mass and the band-gap energy of the semiconductor material.

The conf i nement potential,V(r),is:

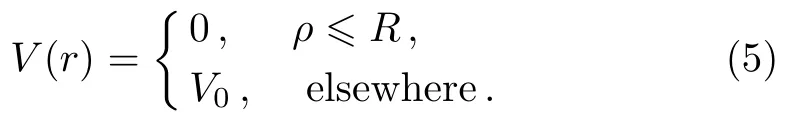
The band-gap discontinuity in(In,Ga)N/GaN system is distributed about 70%on the conduction band and 30%on the valence band.V0denotes the potential barrier,which is given as:

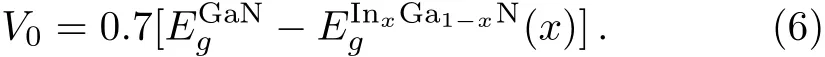
The dependence of the ternary alloy band-gap energy versus the indium composition is governed by the following formulas reported in the recent work of Moses et al.[23]

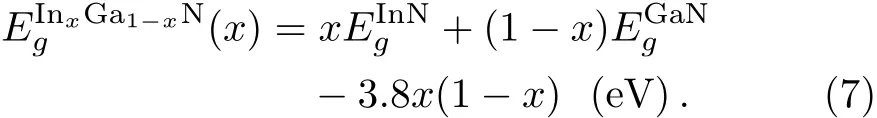
Notice that the eあective-mass and the dielectric constant in ternary alloy are considered as the linear combination of those of GaN and InN semiconductor materials.

Using the eあective units,the eあective Rydberg energy(R∗=m∗e4/2ħ2ε20)and the eあective Bohr radius(a∗= ε0ħ2/m∗e2),the Hamiltonian Hibecomes:

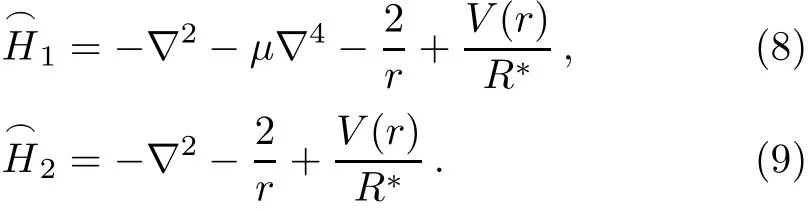
Taking into account of NP eあect and the presence of the impurity,the exact solution of the Schr¨odinger equation is impossible and then,the variational approach is adopted.For the ground-state,the trial wave-function used in our calculation is:

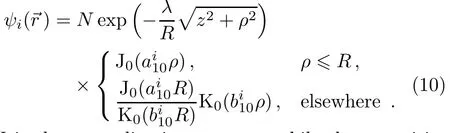
N is the normalization constant while the quantities J0and K0are respectively the zeroth order and the zeroth order modif i ed Bessel functions.The subscript,i≡1,2,correspond to two models described above(H1and H2).In Eq.(10),ai10and bi10are given as:

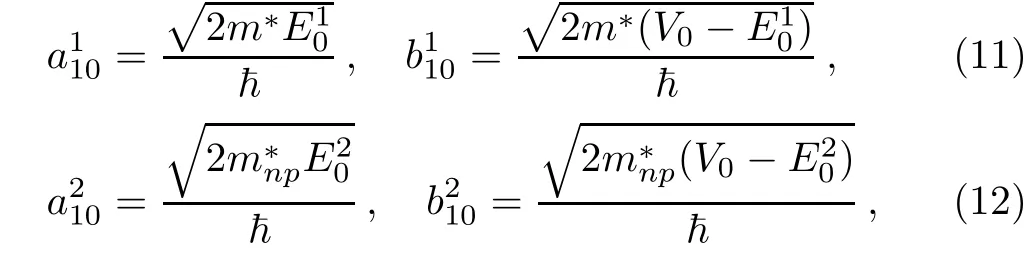
Ei0is the ground-state energy and λ is the variational parameter.The f i rst term in Eq.(10)describes the electronimpurity correlation while the second term is the exact solution of the unperturbed system.

The energy is obtained by minimization with respect to the variational parameter λ.Then,hydrogenic shallowdonor binding energy can be obtained by the following expression:

3 Results and Discussion

Ground-state binding energy in(In,Ga)N cylindrical wire embedded in GaN matrix is calculated as a function of system radius.For well and barrier regions,we have used respectively the material parameters of InxGa1−xN and GaN since their physical parameters are well known and are used in our previous works.[24−25]The diあerence between the band gaps of GaN and InxGa1−xN is ΔEg(x)= (4.51x − 2.66x2). The eあective dielectric constant and the eあective-mass in ternary alloy are given respectively as ε∗(x)=(9.8+3.9x)and m∗(x)=(0.19−0.09x)m0while m0is the free electron mass.Using the above given parameters of In0.2Ga0.8N,one can obtain respectively a∗and R∗as≃ 2.80 nm and≃ 26.65 meV.The spin-orbit splitting energy in InxGa1−xN is obtained as the linear combination of those of GaN(15.5 meV:[26])and InN(5 meV[26]).Notice that the results we presented below are given in the eあective units.

The shallow-donor ground-state binding energy is presented in Fig.1 versus In0.2Ga0.8N/GaN wire radius at room temperature.The conduction band-edge NP eあect is investigated through two models.It appears that for two cases,with and without non-parabolicity eあect,the binding energy increases,reaches a maximum for a wire radius around the eあective Bohr radius,and then decreases as a function of the QWW radius for f i nally,to converge to the corresponding value of(In,Ga)N bulk material for a large value of wire radius.As the wire radius approaches zero(ρ ≪ a∗),the conf i nement becomes negligibly small,and in the f i nite barrier situation the tunneling phenomenon becomes huge and dominant.The binding energy again approaches the bulk value of the barrier region(GaN).

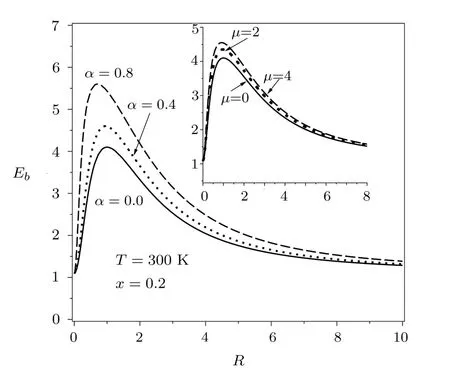
Fig.1 Hydrogenic shallow-donor impurity ground-state binding energy as a function of In0.2Ga0.8N/GaN wire radius.The conduction band-edge non-parabolicity eあects are included for two models.

According to the same f i gure,for both models,one can see that the main eあect of the conduction band-edge NP is to enhance the binding energy for all wire radii.But,this eあect is more signif i cant in narrow wire and it is less sensitive for a large wire.Our numerical results show that for a specif i c value of potential barrier(x=0.2),the maximum of the binding energy moves towards the smaller radii according to band-edge NP parameter.This behavior can be explained by the fact that band-edge NP eあect decreases the energy eigenvalues and the spatial extent of electron wave-function,which reduces the tunneling eあect and then the binding energy can only increase.The displacement of the binding energy peak to narrow wire can be attributed to the eあective Bohr radius or spatial extent drop under the band-edge NP eあect.

The results we have presented above are in good agreement with those reported in literature concerning different LDS-shapes especially for GaAs/(Al,Ga)As and GaN/(Ga,Al)N semiconductor materials.[17−21]

According to Fig.1,it appears that the upward shifts of shallow-donor ground-state binding energy due to the band-edge NP eあect are quantitatively diあerent and depend of the wire radius.To get a good picture of this eあect,we have plotted in Fig.2 the diあerence between the binding energies corresponding to with and without band-edge NP eあect as a function of the wire radius.This diあerence is def i ned as ΔEb(µ)=Eb(µ) − Eb(0)(ΔEb(α)=Eb(α)− Eb(0))for µ =2,4(α =0.4,0.8),which constitutes the direct measure of the band-edge NP eあect.It is clear that this diあerence is dramatically affected by the wire radius and its behavior is the same as that of the binding energy versus the wire radius.This eあect is more marked and reaches its maximum in wire of radius around the eあective Bohr radius while it is less sensitive for large(ρ ≫ a∗)and narrow(ρ ≪ a∗)wires as expected.This result conf i rms that obtained in Fig.1.Notice also that the conduction band-edge NP eあect depends of the adopted model.

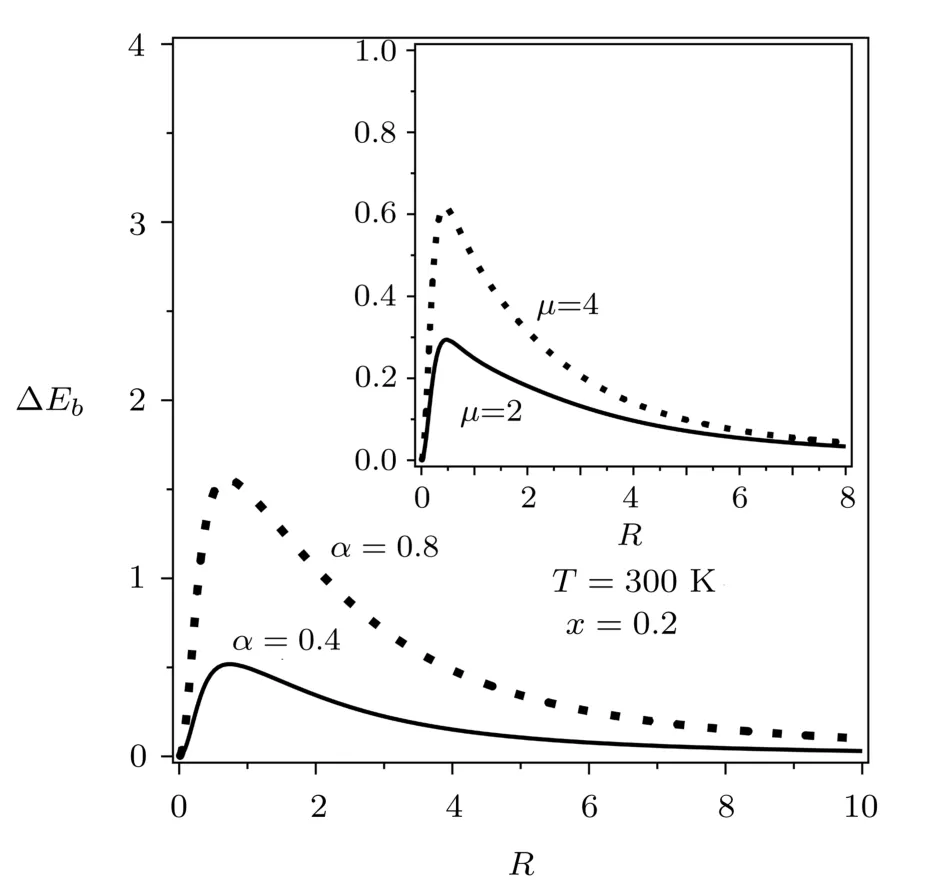
Fig.2 The shallow-donor ground-state binding energies diあerence as a function of the In0.2Ga0.8N/GaN wire radius at room temperature.The band-edge nonparabolicity eあect is also included for both models.

4 Conclusion

Based on variational approach,the ground-state binding energy of con fi ned shallow-donor in ZB In0.2Ga0.8N/GaN cylindrical QWWs is calculated with fi nite potential barrier.The conduction band-edge nonparabolicity and system size eあects are investigated within the framework of single band eあective-mass approximation with one-parametric 1S-like hydrogenic trial wavefunction.The band-edge NP eあect is included through two models.Our results show that the NP eあect:

(i)Is more obvious in the wire of radius around the eあective Bohr radius.

(ii)Is less marked in narrow and large wires.

(iii)Induces a displacement of the binding energy peak to narrow wire.

[1]G.Bastard,Phys.Rev.B 24(1981)4714.

[2]S.Baskoutas and A.F.Terzis,Eur.Phys.J.B 69(2009)237.

[3]H.El Ghazi,I.Zorkani,and A.Jorio,Physica B 412(2013)87.

[4]S.Baskoutas and A.F.Terzis,J.Comput.Theor.Nanosci.7(2010)492.

[5]Z.Zeng,C.S.Garoufalis,and S.Baskoutas,J.Phys.D:Appl.Phys.45(2012)235102.

[6]H.El Ghazi,A.Jorio,and I.Zorkani,Physica B 410(2013)49.

[7]P.G.Moses and C.G.Van De Wall,Appl.Phys.Lett.96(2010)021908.

[8]P.Baser,S.Elagoz,D.Kartal,and H.D.Karki,Superlatt.Microstru.49(2011)497.

[9]P.Baser,I.Altuntas,and S.Elagoz,Fen Bilimleri Dergisi 23(2011)171.

[10]P.Baser,S.Elagoz,and N.Baraz,Physica E 44(2011)356.

[11]N.Esuanu and E.C.Niculescu,U.P.B.Sci.Bull.72(2010)21.

[12]N.Esuanu,E.C.Niculescu,and L.M.Bureleanu,Physica E 41(2009)1386.

[13]E.Tangarife,S.Y.Lopez,M.De Dios-Leyva,L.E.Oliveira,and C.A.Duque,Microelectro.J.39(2008)431.

[14]P.Villamil,C.Cabra,and N.Porras-Montenegro,Microelectro.J.39(2008)466.

[15]S.T.Perez-Merchancano,R.Franco,and J.Silva-Valencia,Microelectro.J.39(2008)383.

[16]S.Dalgic and B.Ozkapi,J.Optoelect.Adv.Matt.11(2009)2120.

[17]G.Rezaei,N.A.Doostimotlagh,and B.Veseghi,Commun.Theor.Phys.56(2011)377.

[18]S.Panda and B.K.Panda,Pramana J.Phys.78(2012)827.

[19]M.Revathi and A.J.Peter,Int.J.Nanaoparticles 5(2012)7.

[20]S.Chaudhuri and K.K.Bajaj,Phys.Rev.B 29(1984)1803.

[21]A.M.Elabsy and P.Csavinszky,Int.J.Quant.Chem.30(1996)1719.

[22]M.K.Bose,K.Midya,and C.Bose,J.Appl.Phys.101(2007)054315.

[23]P.G.Moses and C.G.Van De Wall,Appl.Phys.Lett.96(2010)021908.

[24]H.El Ghazi,A.Jorio,and I.Zorkani,Physica B:Cond.Matt.427(2013)106.

[25]H.El Ghazi,A.Jorio,and I.Zorkani,Physica B:Cond.Matt.426(2013)155.

[26]I.Vurgftman and J.R.Meyer,J.Appl.Phys.94(2003)3675.