针对带局部夹套卧式容器的应力及可靠性分析
2014-03-12时黛
时 黛
针对带局部夹套卧式容器的应力及可靠性分析
时 黛
(内蒙古民族大学机械工程学院,内蒙古 通辽 028000)
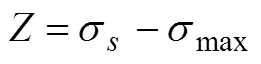
局部夹套;应力分析;可靠性分析;可靠度
压力容器是指工业生产中完成反应、传质、传热、分离和储存等生产工艺功能并承受一定压力的设备。压力容器广泛应用在石油化学工业、能源工业、科研和军工等国民经济的各个部门。在压力容器的使用过程中,由于介质、密封及承压等原因,经常会存在表面裂纹,这些裂纹在疲劳载荷的作用下会继续扩展,最后可能造成压力容器的爆裂而引起事故而危及人员、设备和财产的安全及污染环境的事故。随着机械及化工行业的发展,许多设备需要承受交变载荷,考虑到外载荷、几何形状、尺寸、材料性能等方面存在着一定的随机性和模糊性,以及在认识上的不完善、不准确等原因,导致设备疲劳损伤和耐久性问题的不确定性,从而影响结构的可靠度[1]。为了提高设备的可靠性,研究其失效的原因、掌握设备的失效规律是很重要的,本文在应力分析的基础上对某带局部夹套的卧式容器进行可靠性分析计算。
1 应力分析
在卧式容器中,常常会采用局部夹套对容器内的介质进行加热或冷却,但在使用过程中,夹套与筒体连接焊缝处容易开裂或筒体局部失稳发生,因此有必要从强度方面利对这类容器进行应力分析。
1.1 问题描述


1.2 问题分析
本模型根据结构的对称性选取容器的1/4采用自底向上的实体建模方法,进行分析计算。由于夹套与筒体连接部位是问题的关键,所以对除此之外的部件做如下简化:封头简化为一小段较厚的圆筒,取当量圆筒的厚度为30 mm,长度为100 mm;其次,鞍座在很大程度上增加了夹套的刚度,尤其在夹套附近,为此假定夹套在鞍座垫板部位刚性固定。
在实际生产运行中,卧式容器除受到介质的静压力载荷外,介质重量也会对其产生影响,但此处只分析由介质压力造成的应力,所以只要在与筒体、夹套介质接触的面上加相应的面力即可,而内外壁同时接触两种介质的部位,其面力大小可取为介质的压差[3]。由于封头以较厚圆筒代替,为了使压力作用下产生的最大应力强度更加接近实际,因此在筒体端部各节点施加当量集中力C来模拟封头的端部效应,该集中力的大小可按如下公式计算:
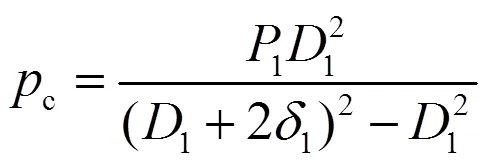
有限元分析的目的是了解模型对外部施加载荷的响应。正确地识别和定义载荷,并有效地实现仿真加载,是运用有限元分析工具的关键一步。利用ANSYS后处理功能[4],求解得该模型的应力强度结果,如图2所示,图中应力大小分别采用不同颜色表示,其中红色表示应力值最大,蓝色表示应力值最小,从应力云图上可以看出最大应力发生在夹套堵板与筒体连接位置靠上的部分,最大应力强度值为184.757 MPa。
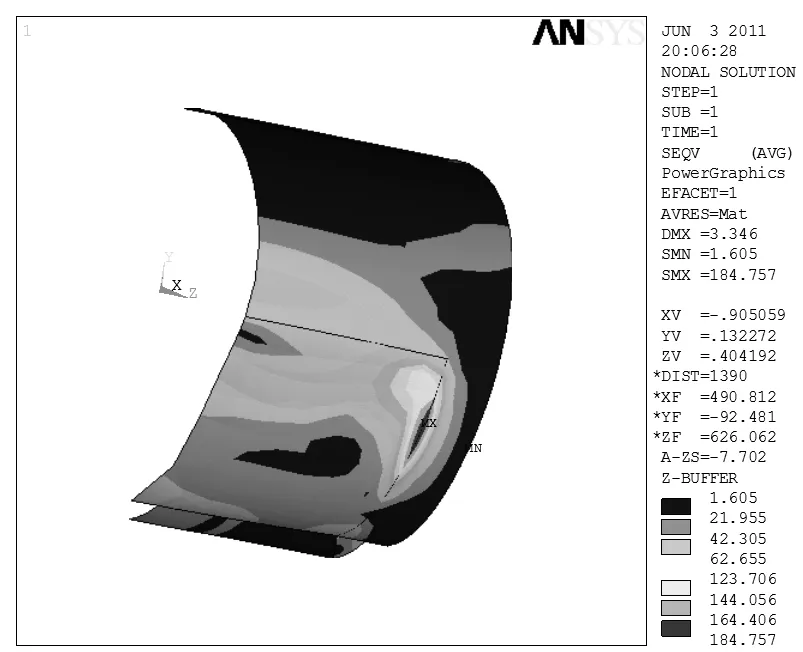
图2 应力强度分布云图
Fig.2 Distribution of stress intensity
2 可靠性分析
2.1 基本方法
在可靠性分析的方法中,蒙特卡罗法的拉丁超立方法应用较多,其效率较直接法高(与直接法相比,避免了重复抽样),本文中就采用了蒙特卡罗法中的拉丁超立方法对该结构进行了可靠性分析,经过以上的应力分析,指定概率分析文件后定义随机变量,进行可靠性分析。

则结构的累积失效概率为:

其中:()—随机矢量的联合概率密度函数。
2.2 随机变量参数计算
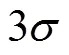
依此处理方法,计算得出结构尺寸和载荷分布参数的计算结果见表1,有了工作压力和屈服强度的分布参数,就可以开始对它们抽样。

表1 随机变量参数及分布
2.3 可靠性分析结果


图3 Z在置信度为95%的情形下的分布图
获得了该带有局部夹套卧式容器在置信度为95%的情形下,<0的概率平均值为3.264 8% ,即说明容器的可靠度为96.735 2%;同时绘制随机输出。
结果参数的灵敏度图如图4所示,从图中可以清楚地看到随机输入参数对输出结果参数的影响程度,影响最大的参数是筒体的压力,其次是屈服极限均值,其余各参数影响较小,可以认为是常数值,因此在容器设计或制造过程中,要特别注意材料的选择。通过以上分析可知该生产车间的带有局部夹套卧式容器是可以正常投入使用,其安全性是有保障的。

图4 输出结果参数的灵敏度图
3 结论
本文通过对典型结构带局部夹套的卧式圆筒形容器的算例分析计算,得到了该压力容器的应力云分布图,由应力强度条件可知,该带局部夹套的卧式圆筒形容器最大应力位置处满足应力强度条件,通过应力分析得出以下结论:
(1)利用软件ANSYS对带局部夹套的卧式圆筒形容器进行了有限元建模,通过应力强度分析获得最大应力的节点位置,得到最大应力发生在筒体最高位置与接管的连接处,即节点为56位置处为疲劳失效的最危险点,其最大应力强度值是184.757 MPa。
(2)在应力分析的基础上对该带局部夹套的容器进行了可靠性分析,通过分析获得了该容器在置信度为95%且初值极限状态<0的情形下时的概率平均值为3.264 8%,即说明容器的可靠度为96.7352%,因此该带局部夹套的卧式圆筒形容器是安全可靠的。
(3)得到了影响该容器可靠性的主要参数是设备的操作压力和设备材料的屈服强度,所以在条件允许的情况下,应该尽量选用屈服极限较高的材料。
4 结束语
利用ANSYS对复杂结构进行可靠性分析是可行的,其方法简单、避免了大量试验、节约了资源,是有限元理论和可靠性分析理论的有机结合,为复杂结构的可靠性分析提供了新的方法。它可以客观反映设备的可靠性水平,并为设备的可靠性水平提高提供科学的依据,因此有限元分析方法必将给化工装备结构设计带来新的发展,计算机辅助分析将是化工装备设计的未来发展方向。
我们相信,随着计算机技术和有限元技术的不断发展,我国钢制压力容器的分析设计的应用将会更加普及和广泛,以满足石油与石油化学工业、核能工业、冶金工业、机械工业等行业的迅速发展对压力容器大型化、复杂化、高参数的需求。而利用有限元软件对其进行相应的分析以确保容器能安全的运行也会起着越来越重要的作用!
[1]武拴男,杨兆建. 机械可靠性设计有关问题探讨与应用研究[J].机械工程与自动化,2009,25(5):101-102.
[2]余伟炜,高炳军. ANSYS在机械与化工装备中的应用[M]. 北京:中国水利水电出版社, 2006.
[3]林国庆,王茂廷. 基于ANSYS中Monte-Carlo 法对带局部夹套卧式容器的可靠性分析[J]. 轻工机械,2012,30(1):99-~102.
[4]秦宇. ANSYS 11.0基础与实例教程[M]. 北京:化学工业出版社,2009.
[5]林有志,刘凌霜,宋爱斌等. 机械可靠性设计的研究现状与进展[J].科学之友,2009,17(6):3-4.
[6]刘惟信. 机械可靠性设计[M].北京:清华大学出版社,1996.
[7]李兆锋, 江楠.基于有限元法对带接管压力容器的可靠性分析[J].石油化工设备技术,2011,40(1):21-25.
[8]林国庆,王茂廷,林猛.汽车发动机连杆在拉压工况下的可靠性分析[J].辽宁石油化工大学学报,2011,31(3):50-53.
Stress and Reliability Analysis of Horizontal Container With Local Jacket
(College of Mechanical Engineering, Inner Mongolia University for the Nationalities, Inner Mongolia Tongliao 028000,China)
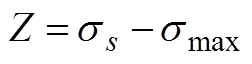
Local jacket; Stress analysis; Reliability analysis; Reliability
TQ 051
A
1671-0460(2014)06-1015-03
2014-03-28
时黛(1986-),女,辽宁抚顺人,助教,硕士,2012年毕业于辽宁石油化工大学化工过程机械专业,研究方向:设备安全。E-mail:10dai@163.com。
