基于L-M优化算法的猪舍氨气浓度预测模型研究

谢秋菊，苏中滨，刘佳荟，郑 萍，马铁民，王 雪

（1.东北农业大学电气与信息学院，哈尔滨 150030；2.黑龙江八一农垦大学信息技术学院，黑龙江 大庆 163319；3.索尼信息系统（大连）有限公司，辽宁 大连 116085）

猪舍环境因素包括：空气温湿度、通风、光照、粉尘、有害气体等[1]。氨气是反映猪舍空气环境的一项重要指标。氨气浓度持续超过一定限制值时，会对猪的呼吸系统及中枢系统造成危害，影响猪生长性能、降低饲料利用率和种猪繁殖性能。对于猪舍环境的预测及控制己引起广泛关注[2]。国内外研究者对不同条件下，猪舍内氨气变化情况做大量研究工作[3-7]，Ni等对猪舍内氨气散发进行测量，建立氨气散发模型[8]，葛广军等对猪舍内一年中不同月份氨气的排放量研究[9]。黄建清基于BP神经网络对测量养殖环境中缺失的氨气数据恢复[2]。但是由于氨气浓度受舍内温湿度和通风等环境因素影响，难以建立准确预测模型。仅依靠监测设备对舍内氨气浓度监测，虽可获取氨气浓度数据，但存在调控滞后性问题，未对猪舍内氨气浓度建立有效的预测模型。

本文针对规模化养猪场中猪舍内环境参数进行采集，根据采集数据基于L-M优化算法建立BP神经网络氨气浓度预测模型。采用传统梯度下降方法，网络收敛速度慢、效率低[2]。本文采用L-M优化算法建立的模型收敛速率快，预测误差与实际数据验证误差很小，可实现猪舍氨气浓度预测，为猪舍氨气浓度控制及预警提供技术支持。

1 L-M优化算法

1.1 BP神经网络的结构及训练方法

BP（Back propagation）神经网络是Rumelhart和McCelland等于1986年提出，是目前应用广泛的神经网络模型之一，按误差逆传播算法训练多层前馈网络[10]。BP神经网络模型拓扑结构包括输入层（Input）、隐层（Hide layer）和输出层（Output layer）[11]。输入层各神经元负责接收来自外界的输入信息，传递给中间层各神经元；中间层是内部信息处理层，负责信息变换，根据信息变化能力需求，中间层设计为单隐层或者多隐层结构；最后一个隐层传递到输出层各神经元的信息，经进一步处理后，完成一次学习的正向传播处理过程，由输出层向外界输出信息处理结果。为确定神经网络输入与输出关系，需选定神经网络层次、各层的节点数、转移函数及确定各层间节点连接权值。

BP网络训练过程是由正向传播和误差反向传播组成。给定网络一组输入样本，BP网络依次对输入样本中的每个输入样本进行训练。主要过程是：对于一组输入样本，通过BP神经网络计算实际输出。用BP网络实际输出与输出样本间误差修正网络连接权值，直至二者误差达到设定值[12-14]。这一较小值称拟合误差，一般用实际输出与输出样本间误差平方和表示，即：

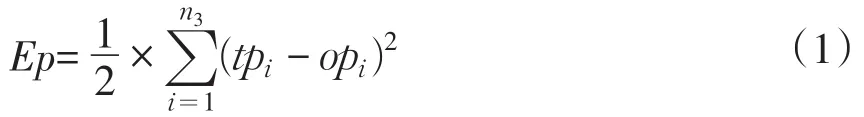
公式（1）式称为误差函数，tpi样本的输出值；opi为实际输出值。

1.2 L-M优化算法

BP神经网络可无限逼近非线性函数，但收敛速度慢、易陷入局部极小值和网络学习不稳定。L-M优化算法可改进BP神经网络缺陷，加速网络收敛速度、提高网络训练精度。

L-M（Levenberg-Marquardt）优化算法是梯度下降法和牛顿法的结合，结合梯度下降法在开始几步时下降速度较快和牛顿法在最优值附近可产生理想搜索方向特点。L-M优化算法搜索方向定义为：

令η(k)=1，则X(k+1)=X(k)+S（X(k)）

开始时，λ取一个很大的数值，此时的L-M优化算法相当于步长很小的梯度下降法；随着最优点的接近，λ减小到零，搜索方向从负梯度方向转向牛顿法方向。

L-M优化算法迭代过程如下[15-16]：

其中，z（i）表示第i次迭代的权值和阈值组成的向量，z（i+1）是第i+1次权值和阈值组成的向量。

对于牛顿法，Δz=-[∇2E（z）]-1·∇E（z）， ∇E（z）为梯度。

设误差评价函数为：

公式（4）中，ei（x）为误差。

对于高斯牛顿法有

公式（7）中，比例系数μ＞0为常数，J为单位矩阵。

L-M优化算法在迭代时，首先给出训练误差允许值ε、β、μ，以及初始化权值和阈值向量z（0），然后计算出（3）式，K和（7）式的值，最后计算出E（x），当E（x）＜ε时迭代停止；否则令k=k+1，μ=，继续迭代，直到E（x）＜ε为止。

猪舍氨气浓度变化受舍内多个环境因素影响，具有时变和延时特性，根据猪舍环境调控应用需求，本文针对基于梯度下降的BP神经网络预测方法训练时间长、精度低等问题，采用L-M优化算法对BP神经网络存在缺陷进行改进，提高网络收敛速度和训练精度。

2 基于L-M优化算法的猪舍氨气浓度预测模型

由于氨气浓度受舍内温湿度、通风、猪舍结构等环境因素影响，本文选取温度、湿度、风速和氨气浓度作为猪舍环境监测因素，建立环境预警模型。由于猪舍环境因素与时间、空间等多种影响因素相关，各因素间相互作用，是非线性系统。基于L-M优化算法的BP神经网络能有效地将非线性模型中的输入与输出之间内部蕴含规律进行映射，可任意精度逼近任意函数，因此本文基于L-M优化算法，对猪舍的环境进行预测，根据预测模型可以建立相应的预警措施。

2.1 数据采集

数据采集是监测和预警的基础，猪舍环境数据采集是在猪舍内合理布置传感器节点，对节点采集的有效数据通过数据融合获得当前环境数据值。本文环境监测数据取自黑龙江大庆市某规模化养猪场的哺乳母猪舍，从2013年3月1日至2013年5月1日连续对猪舍内环境进行监测。猪舍建筑样式为密闭式、南北朝向，长度为70 m，南北跨度为10 m，高度为5 m，双列式钢质围栏，舍内饲养母猪数量为60头，仔猪数量为200头。在猪舍内不同位置分别布置6个数据采集节点，分别放置在两列围栏的两端和中间位置，高度为1 m，传感器布置如图1所示。每个节点同时对温度、湿度和氨气浓度采集，温湿度采集选用SHT10温湿度传感器，氨气浓度采集选用ME3-NH3电化学氨气传感器，猪舍环境数据现场采集设备如图2。每间隔10 min对猪舍内环境数据进行一次采集，由于在舍内布置多个采集节点，需对这些节点数据进行处理，本文将同一时刻同种类传感器数据利用求加权平均值的方法处理，作为舍内环境实时数据。

图1 猪舍环境数据采集节点布置Fig.1 Layout of barn environmental data collection nodes

图2 猪舍环境数据现场采集图像Fig.2 Photo of piggery environmental data collection

设猪舍中的6个采样节点分别为x1，x2，…，x6，每个节点的信息表示为xi（ti，hi，ni，ωi），其中：ti，hi，ni，ωi分别表示节点xi某时刻的温度值、湿度值、氨气浓度及权重[17]。由于猪舍的温湿度、氨气浓度一般会在入口处数值较低，依据距离猪舍入口距离远近不同，传感器权重ωi取值如公式（8）所示。某时刻牛舍内的温度T、湿度H、氨气N，则可表示为公式（9）、（10）和（11）所示。

在公式（8）中，mi为传感器距离猪舍入口的距离。

将T，H，N的值作为猪舍某时刻的环境数值存入数据库，作为环境预测模型的输入数据。

本文在连续采集的2个月环境数据中，选取其中30 d的温度、湿度、风速和氨气浓度数据，将这些环境数据每隔60 min进行求平均值处理，共得到720组数据，部分数据如表1所示。

表1 猪舍环境数据Table 1 Piggery environmental data

2.2 猪舍氨气浓度预测模型的建立

2.2.1 预测模型数据预处理

由于母猪的生长周期长，猪舍四季温湿度变化较大，为反映近期猪舍环境变化规律，选取训练数据和测试数据的时间跨度不宜过长。在对网络模型进行训练之前，首先需要对网络的样本数据进行归一化处理[18]，将数据变换为（0，1）区间的值，归一化处理采用最大最小算法，如公式（12）所示。

公式（12）中，xi表示输入数据，xmin表示数据的最小值，xmax表示数据的最大值。

2.2.2 预测模型的结构

BP网络的泛化能力与网络隐层数和隐层节点数有关。虽然隐层数目增加可以提高网络的非线性影射能力，但是隐层数目超过一定值时，反而会降低网络性能[19]。因此，隐层数要尽量简单，具有较强的泛化能力[20]。本文设计三层BP网络结构，如图3所示。输入层的节点分别为影响环境质量的主要因素：温度、湿度和风速，输入层神经元个数为3；根据Kolmogorov定理、设计者的经验和多次试验，证明隐层神经元个数为7时逼近效果最好；输出层是氨气浓度，输出层神经元个数为1。网络结构为3-7-1三层结构。隐层神经元的传递函数为S型正切函数tansig，输出层神经元传递函数采用S型对数函数logsig[21]。

图3 模型结构Fig.3 Model structure

以前29 d实测并经过归一化处理的696组温度、湿度和风速数据作为网络输入样本，网络的输出样本为696组数据对应的实测氨气浓度数据，以第30天24组实测并经过归一化处理的温度、湿度和风速数据作为测试样本。通过Matlab建立三层结构BP神经网络，使用L-M优化算法对网络进行训练，设定网络训练步数为1000，性能目标误差为0.001，学习速率为0.05，动量常数为0.9。

2.3 模型预测结果与实测数据验证分析

由于对网络训练采用L-M算法，网络收敛速度很快，模型完全达到设计性能，网络在经过90步训练后，对696组训练数据达到目标误差，模型训练性能如图4所示。

图4 网络训练性能Fig.4 Performance of network training

本模型对24组测试数据进行氨气浓度的预测，预测值与实际值验证如图5所示。

图5 网络预测值与实测值对比Fig.5 Comparison between network prediction and actual value

表2 预测模型验证Table 2 Verification of prediction model

由图4、5和表2可以看出，基于L-M优化算法预测模型最大相对误差为1.72%，最小相对误差为0.11%，平均相对误差为0.57%，相关性R=0.99337；线性预测方法最大相对误差为6.34%，最小相对误差为2.05%，平均相对误差为3.62%，相关性R=0.95142。因此，基于L-M优化算法预测模型性能良好，预测值与实际测量值相对误差很小，能够满足猪舍氨气浓度预测的需求。

3 结论

本文建立的预测模型对受多环境因素影响的猪舍氨气浓度预测，实际环境数据作为输入样本及测试样本，对样本训练采用L-M优化算法，经过90步训练达到预定误差。通过预测值与实际测值对比试验研究结果表明，网络收敛速度快，最大相对误差仅为1.72%，与线性预测方法相比提高猪舍氨气浓度预测准确性与及时性，可为猪舍环境预警及控制提供数据技术支持。

[1] 黄建清.具有缺失数据恢复估算的畜禽养殖有害物质数据处理系统设计[D].镇江:江苏大学,2009.

[2] 陈长喜,张宏福,王兆毅,等.畜禽健康养殖预警体系研究与应用[J].农业工程学报,2010,26(11):215-220．

[3] Seedorf J,Hartung J,Schroder M,et al.Concentrations and emissions of airborne Endotoxins and microorganisms in livestock buildings in Northern Europe[J].Agric Engng Res,1998,70:97-109.

[4] Angelika H,Eberhard H,Thomas J,et al.Cooling effects and evaporation characteristics of fogging systems in an experimental piggery[J].Biosystems Engineering,2007(97):395-405.

[5] Farmer C,Devillers N,Widowski T,et al.Impacts of a modified farrowing pen design on sow and litter performances and air quality during two seasons[J].Livestock Science,2006(104):303-312.

[6] Ki Y K,Chi N K.Airborne microbiological characteristics in public buildings of Korea[J].Building and Environment,2007(42):2188-2196.

[7] 王宗尉.舍内环境与猪健康水平多元回归模型分析[D].哈尔滨:东北农业大学,2009.

[8] Ni J Q,Vinckier C,Coenegrachts J,et al.Effect of manure on ammonia emission from a fattening pig house with partly slatted floor[J].Livestock Production Science,1999,59:25-31.

[9] 葛广军.畜禽饲养场环境测控系统及数据处理的研究[D].镇江:江苏大学,2006.

[10] Rumelhart D E,Mcclelland J L.Parallel distributed processing[M].Cambridge:The MITPress,1986.

[11] 田景文,高美娟.人工神经网络算法研究及应用[M].北京:北京理工大学出版社,2006.

[12] Atiya A,Ji C Y.How initial conditions affect generalization performance in large networks[J].IEEETrans Neural Networks,1997,8(2):448-451.

[13] 江学军,唐焕文.前馈神经网络泛化能力的系统分析[J].系统工程理论与实践,2000,20(8):36-40.

[14] 张兵,袁寿其,成立,等.基于L-M优化算法的BP神经网络的作物需水量预测模型[J].农业工程学报,2004,20(6):73-76.

[15] 王建梅,覃文忠.基于L-M算法的BP神经网络分类器[J].武汉大学学报:信息科学版,2005,30(10):85-88.

[16] 项文强,张华,王姮,等.基于L-M算法的BP网络在变压器故障诊断中的应用[J].电力系统保护与控制,2011,39(8):100-111.

[17] 王雷雨,孙瑞志,曹振丽.畜禽健康养殖中环境监测及预警系统研究[J].农机化研究,2012,10:199-203.

[18] 李秀金.养殖场气味的产生及控制技术[J].农业工程学报,2001(9):78-81.

[19] 田大钢.前馈神经网络的学习能力[J].系统工程理论与实践,2005(5):105-109.

[20] Bogdan M W,Chen Y X.Effieient algorithm for training neural networks with one hidden layer[A].M A leks-andered.Proc of the Int,1Joint Conf on Neural Networks Vol.31[C].Washington D C:IEEE Press,1999:1725-1728.

[21] 飞恩科技术产品研发中心.神经网络理论与MATLAB 7实现[M].北京:电子工业出版社,2005.