回归课堂本色凸显数学本质

徐玮玮

随着新课改向纵深发展，真实有效的数学课堂已成为广大数学教师的追求目标。课改初，我们走了不少弯路，比如过于注重形式，追求表面的热闹，淡化了数学教学的本质，致使学生的思维得不到应有的发展，教学效率低下，等等。现在，在追“新”的过程中，越来越多的教师更多地开始关注并深入地思考课堂中暴露出来的一些问题，使数学课堂得到了理性的回归，发生了质的变化。课堂逐步开始去包装，存本色，有“数学味”，实现了“原生态”的教学方式。

一、教学内容回归实效

新课程改革强调教学内容利用情境进行引入，但由于对课程资源的开发和利用缺乏有效把握的经验，在实施层面上便出现了教学内容的泛化现象。

例如，教学《函数的单调性》时，有一位教师先让学生作出函数f（x）=x和函数f（x）=x2的图像，接着提问：观察这两幅图，你能得到哪些结论？生1：f（x）=x的图像是直线，f（x）=x2的图像是抛物线。师：很好。生2：f（x）=x的图像经过原点，f（x）=x2的顶点是原点。生3：f（x）=x的图像关于原点中心对称，f（x）=x2的图像关于轴对称。师：还有吗？如此没有目标指向性的问题指导，由于没能及时引出本课主题，任由学生发言，泛化下去，所以不能使学生的思维有的放矢，不能直接切入本课的核心环节，为本课学习服务，浪费了宝贵的时间。

另一位教师则先让学生作出函数f（x）=x和函数f（x）=x2的图像，接着提问：观察这两幅图，随着x的增大，图像的变化趋势分别是怎样的？生：f（x）=x的图像上升，f（x）=x2的图像先下降再上升。师：观察用描点法作图时的列表，函数值f（x）随着x的增大是怎样变化的？生：函数f（x）=x中，函数值f（x）随着x的增大而增大。函数f（x）=x2中，当x<0时，函数值f（x）随着x的增大而减小；当x>0时，函数值f（x）随着x的增大而增大。师：一个一般函数y=f（x）在区间（0，+∞）内“图像上升”，“随着x的增大，函数值f（x）增大”，如何用符号语言进行描述呢？（分组讨论后交流）

这段教学紧贴主题，抛弃了对本节课无价值的东西，课堂上更多体现的是真实、有效，让那些盲目的泛化现象得到理性的回归，充满了数学的真实美和智慧美。

二、教学活动回归内化

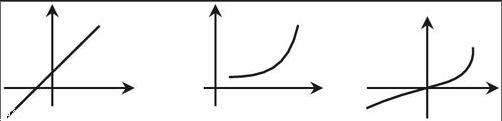
同样是《函数的单调性》的概念教学，有一位教师是这样进行教学的，他先出示如下一组函数图像。

（1） 提问：上述函数图像的变化趋势是怎样的？（小组讨论）

（2） 提问：怎样用数学语言刻画上述函数图像的这一特征呢？（小组讨论）

（3） 教师直接给出增函数的数学定义。

（4） 师生进行定义剖析，提出以下注意点：a.注意函数的单调性是对某个区间而言的；b.特别注意定义中的“给定区间”“属于”“任意”“都有”这几个关键词；c.关注几何特征，单调增（图像从左向右连续上升），单调减（图像从左向右连续下降）。

对于第一个问题，学生很容易就能得出答案，因此第一个讨论设计显得有些多余，在第二个讨论处，由于教师没能及时帮助梳导，所以小组合作讨论流于形式，没有真正发挥学生的合作学习和参与作用，使探究有形无实，学生只是机械地、按部就班地经历探究过程的程序和步骤。在后面进行定义剖析时，尽管教师反复引导学生理解“属于”“任意”这些关键词，学生总是不能体会词的关键作用，想不通少了它们或换一种说法定义会出现什么问题，在这一教学过程中，学生失去了体悟概念发生过程的机会，尽管小组合作学习进行了好几次，但由于缺乏平等的沟通和交流，缺乏深层的交流和碰撞，所以课堂显得有“温度”无“深度”，只“外化”而无“内化”。

对此，教师应抓住问题的关键点，让学生进行深层次的交流与碰撞，激活学生内在的探究思维，让学生全身心地投入探索活动中，真正让教学活动回归内化，这样学生的探究欲望得到了满足，个性得到了充分的发展，真正促进了学生的全面发展。

三、教学层次回归高效

当前课堂教学存在的主要问题有两个，一是教学滞后于学生的发展水平和学习能力（学习潜力），教师常常花很多时间解决学生能够独立解决的问题，这不仅导致教学水平和效益的低下，更为严重的是阻滞学生学习能力的发展；二是教学过分超前于学生的发展水平和学习能力，学生“跳几跳，还摘不到桃”，严重挫伤了学生的学习积极性，长此以往，便失去了学习数学的兴趣。

一位教师在教学《双曲线的标准方程》时，当学生已经熟练掌握了双曲线的标准方程后，出示了这样一道题：求经过点P（3，2），且与双曲线x2 3-y2 4=1有相同渐近线的双曲线的方程。

师：这道题你们解解看。

生：可以用统设法，设所求双曲线方程为x2 3-y2 4=λ（λ≠0）。

生：我用的是分类讨论法，分两种情况，一是焦点在x轴上；二是焦点在y轴上，但有点烦。

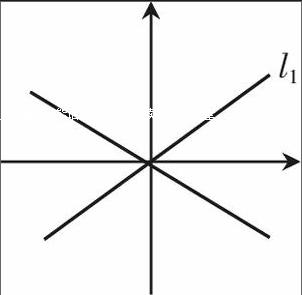
师：这位同学想得很好，分类讨论是因为无法判断焦点的位置，但真的不能判断吗？（教师画图分析）

师：如果点P在l1的下方，焦点在哪个轴上？

生：x轴上。

师：如果点P在l1的上方，焦点类哪个轴上？

生：y轴上。

师：如何判断点P在l1的上方还是下方？

生：将点P坐标代入l1的方程。

以下是另一位教师教学《函数的奇偶性》的片段。

师：回忆初中以来我们学过的平面图形，哪些是轴对称图形？哪些是中心对称图形？（小组讨论）

生：轴对称图形有等腰三角形、等腰梯形、圆、菱形、长方形等。中心对称图形有圆、正方形、菱形、平行四边形、正六边形、椭圆等。

师：回忆初中以来我们学过的函数的图像，哪些函数的图像是轴对称图形？哪些函数的图像是中心对称图形？

生：一次函数的图像是轴对称图形，又是中心对称图形。二次函数的图像是轴对称图形。反比例函数的图像既是轴对称图形，又是中心对称图形。（教师同时提问要求指出对称轴和对称中心）

师：哪些函数的图像以y轴为对称轴？哪些函数的图像以原点为对称中心？用解析式表示函数。（分组讨论）

生：y=x2的图像以y轴为对称轴，y=x的图像以原点为对称中心。（画出它们的图形，引导学生观察图像归纳偶函数、奇函数的图像特征，进而归纳偶函数、奇函数的解析式特征）

……

在这两个过程中，教师紧紧抓住学生的现有发展区和最近发展区来展开。第一个片段中教者没有满足于学生会做即可，而是顺着学生的思路引导学生理解，打开学生解决问题时思维上的结，让学生感触“原来这样做也可以”，使学生明白当思考受阻时不能轻易放弃，再深入一些就迎刃而解了，同时发散了学生的数学思维，激发了学生的学习兴趣。第二个片段中教师放手让学生用自己已有的知识经验，通过认真思考、大胆尝试和同伴互助，一步步完成了对于偶函数、奇函数这两类函数特征的理解。通过这样高层次的数学学习，学生掌握了数学思维的方法，学会了学习。

在新课程改革的前行中，我们教者要充分利用课堂，发挥45分钟的效率，让教学内容更精炼，让教学活动在热闹的表面下更有深度、能启迪学生的思维，让教学层次定位在打开学生思维的“结”上。只有数学课堂回归本色，凸显数学本质，达到促进新课改理念与数学教学的和谐，才能促进学生数学思维的发展。

（责任编辑黄春香）endprint