基于GH-BLADED的风电机组风轮叶片应变分析
2014-03-11李磊苏英霞杨衎
文/李磊 苏英霞 杨衎
基于GH-BLADED的风电机组风轮叶片应变分析
文/李磊 苏英霞 杨衎
风电机组风轮叶片是机组重要零部件,不仅能够产生用于发电的能量,其产生的推力也影响机组的稳定性,所以,叶片的设计准确性突显得日益重要。对于设计与实测的容许偏差要求也越来越高,一般的,弯曲挠度为±7%,应变为±10%。为了保证设计与实测的偏差在容许范围内,设计人员正在寻找一个简单的工程计算方法来保证计算的准确性和实用性。GH-BLADED软件是现今世界上较流行的风电机组设计软件,其结果的准确性在同类软件中名列前茅。尤其在BLADED4.0及以上版本推出以后,叶片的参数精度有较大提高,依据Timoshenko梁理论,允许设计人员考虑叶片剪切刚度及叶片轴向刚度所带来的影响,从而引导叶片设计者以及与叶片设计关系紧密的工程师们用一个新的理念来解读叶片。
本文以HT24型号叶片为实例,通过BLADED软件来模拟叶片在测试状态下叶片挠度并通过此数据推导出叶片的应变量,并与HT24型号叶片实测数据进行对比,验证该方法的准确性。
纯弯曲时,梁横截面的正应力分析
应用弹性范围内的应力-应变关系:σ=E * ε,将正应变分布的数学表达式代入,便得到梁弯曲时横截面上正应力沿横截面高度分布的数学表达式:

式中,E为材料的弹性模量;ρ为中性层的曲率半径,对一个截面而言,也是一个常数,但是一个待定的量。于是,C也是待定的常数:
上式表明,梁弯曲时,横截面上的正应力沿横截面的高度方向从中性轴为零开始呈线性分布的。
纯弯曲时,梁的应变分析
叶片是薄壁结构,长宽与铺层厚度的比值较大,故可采用薄壁杆件结构力学为结构设计理论基础。由于叶片各剖面的铺层相对于翼型厚度很薄,可以将叶片的各剖面看作薄壁翼型,假设铺层中的正应力和剪应力沿其厚度均匀分布。当叶片在受载荷作用发生变形时,横剖面在自身平面上的投影保持不变,但横剖面沿纵向方向可以自由翘曲。由翼型截面决定的中空壳体结构在抵抗非平面内剪切力载荷方面不是很有效的,所以为了保持横剖面的形状,叶片设有剪切腹板,故假设剖面在小变形情况下是符合实际的(如图1所示)。
OA和OB两线元的长度分别为OA=dx,OB=dy。设O点的位移为u(x,y)和v(x,y),A点的位移是u(x+dx,y)和v(x+dx,y),B点的位移是u(x,y+dy)和v(x,y+dy)。根据定义,导出xy平面内的应变分量:

根据叶片剖面摆振力矩、挥舞力矩和轴向力的合内力关系,沿整个剖面全部承受正应力的面积进行积分,可得Z方向(垂直于截面方向)的轴向力、绕x轴和y轴(如图2所示)回转的弯矩:

其中,
Fz为叶片沿z方向的轴向力
σz为轴向正应力
A为截面面积
ε0为截面正应变
E为截面杨氏模量
X为距y轴的距离
Y为距x轴的距离
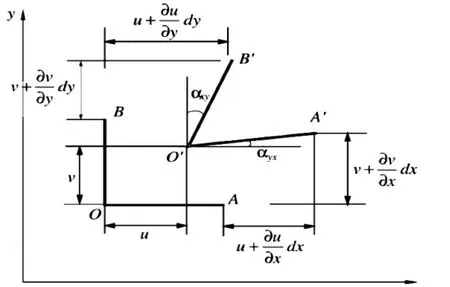
图1 梁的应变分析图示

图2 叶片坐标示意图
ρx为x方向挠度的曲率半径
ρy为y方向挠度的曲率半径
Mx为截面沿x轴的弯矩
My为截面沿y轴的弯矩
Ixx为截面沿x方向的惯性矩
Iyy为截面沿y方向的惯性矩
Ixy为截面惯性积
从而得到,薄壁翼型的各特征点在外载荷作用下的应变矩阵为

GH-BLADED叶片变形的实现
通过blades模块中additional mass/inertial对叶片进行如表1的载荷加载,同时设置叶片的方位角,因叶片重量产生的弯矩约占该截面加载弯矩的20%左右,其产生的影响应考虑在内。
其中,Flap1表示挥舞方向压力面到吸力面方向第一次加载载荷,Flap2表示挥舞方向压力面到吸力面方向第二次加载载荷,Flap3表示挥舞方向吸力面到压力面方向加载载荷,Edge1表示摆振方向后缘到前缘方向第一次加载载荷,Edge1表示摆振方向后缘到前缘方向第二次加载载荷。
通过计算可以求得叶片变形量(如图3-图7所示),通过计算,误差在容许范围之内,满足工程要求。
叶片应变的计算
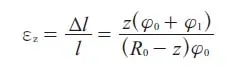
由于R
0
>>z,则有φ
0
* R
0
=ρ * φ
1

从上述梁的应变分析可得,当物体的位移分量完全确定时,形变分量即完全确定。下面以计算Flap1载荷试验时切面14m处的应变为例,使用BLADED软件计算出
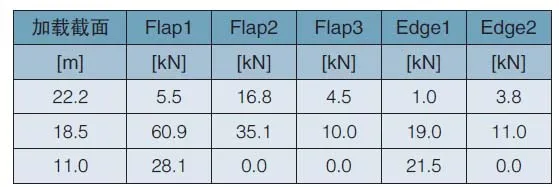
表1 叶片试验及计算加载载荷
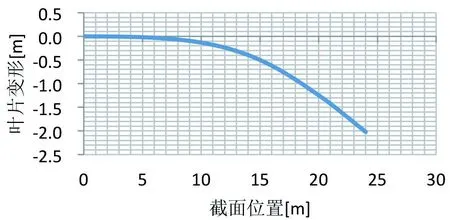
图3 加载载荷Flap1叶片变形图
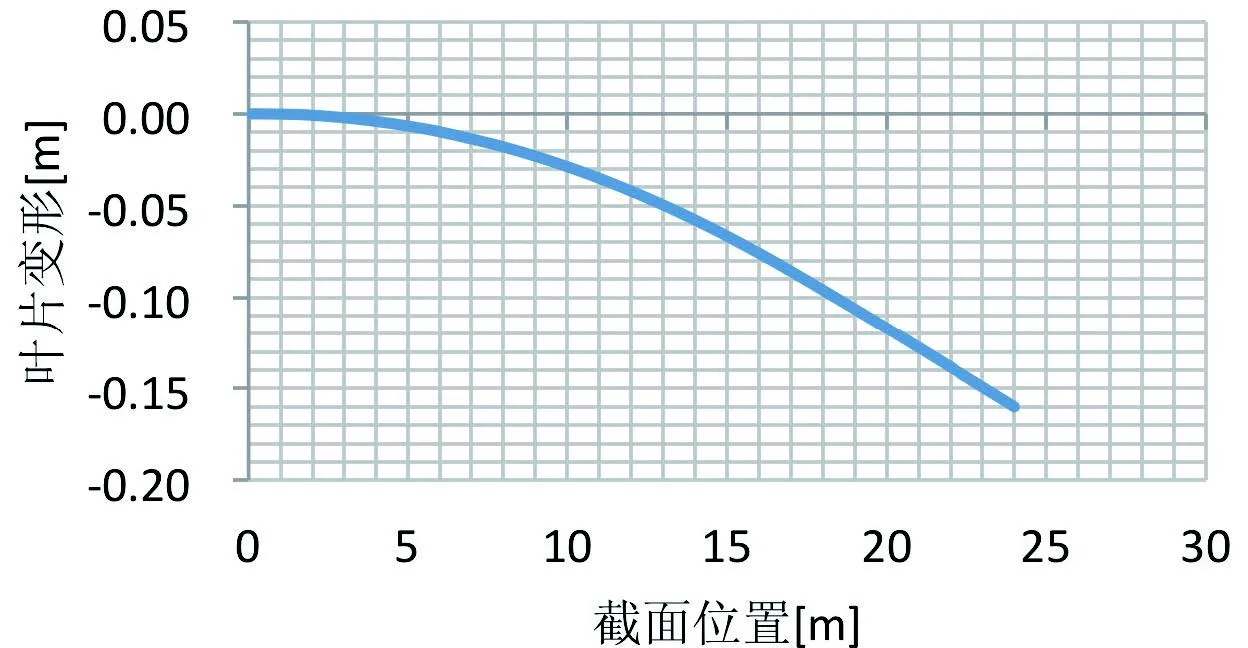
图5 加载载荷Flap3叶片变形图
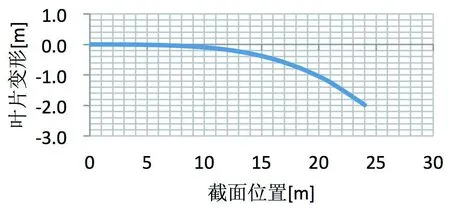
图4 加载载荷Flap2叶片变形图
13.995m,14m,14.005m处的叶片变形量,以此三点做圆,求出曲率半径65.071m,贴应变片的位置距中性面的距离乘以曲率即为此位置的应变。
从而可以计算,在此切面中间位置,中性面距工作面距离为0.118m,应变即为1813μs,中性面距非工作面为0.169m,此处应变即为2597μs,其中μs=10-6。
结论
本文针对风电机组风轮叶片的设计进行了一些探索,为叶片的挠度与应变的计算找到了一种较为普遍的算法。本文使用GH-Bladed软件进行挠度计算,依据经典应变理论计算出叶片的应变,在此基础上,计算结果与HT24型号叶片试验结果进行对比,结果表明本文的方法是有效的。
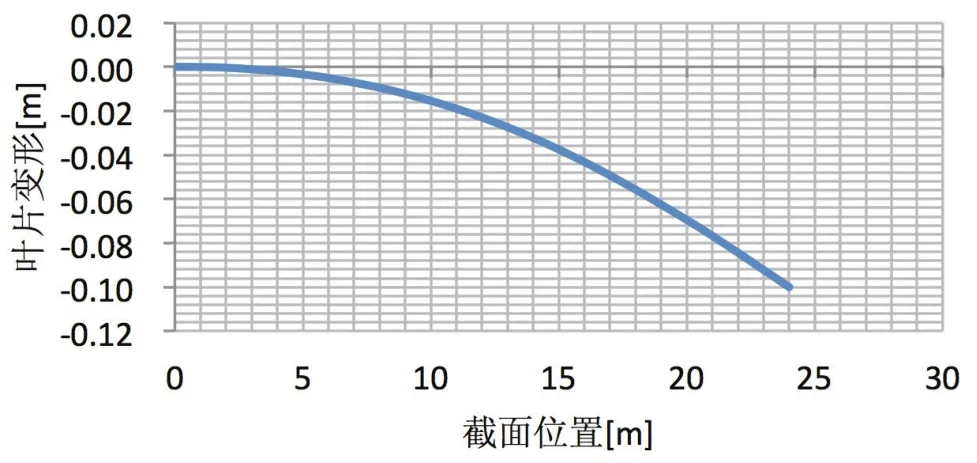
图6 加载载荷Edge1叶片变形图

图7 加载载荷Edge2叶片变形图
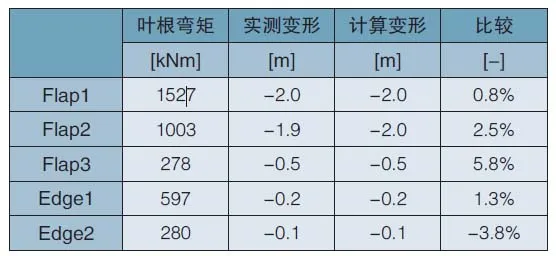
表2 叶片叶尖变形量试验与计算对比

表3 计算应变与实测应变的比较
(作者单位:李磊、苏英霞:中航惠腾风电设备股份有限公司;杨衎:广东粤电湛江风力发电有限公司)

