扰动下的生物质能供应链收益共享契约研究

张潇潇

（同济大学 交通运输工程学院，上海201800）

目前，我国生物发电的原料一般采用秸秆，属于农业生产中的副产物。对于生物发电的原料生产供应链，其结构模式大多采用标准的“公司＋基地＋农户”形式。该模式具体运营为:基地承包一定区域的农户，与农户签订独立合约，收购原料并承担仓储工作；同时，基地作为公司的原料供应商，与公司签订独立合约。与简单的“公司＋农户”形式相比，基地不仅可以更好地整合农户资源，而且在同公司签订合约时改善了单个农户的弱势地位；同时，公司仅需与少量基地建立长期供给关系，降低了原料供给管理成本；基地对原料进行预处理、仓储并组织运输，降低了供应链的物流成本。

虽然是专门的原料种植，但原料不足依然是生物燃料产业和生物燃料供应链共同面临的严重问题。此外，在生物质能供应链环节中，能源公司直接面对市场需求也会产生波动。因此，研究生物质能供应链供给和需求的扰动具有十分重要的意义。

Larivirer和Tsay指出供应链中的无效率运行由外部性导致，即供应链上双重边际化结果——供应链由各个成员共同参与，并且当各成员追求自身利益最大时会与供应链整体利润冲突，因而，需要通过供应链协调和契约设计来提高整体供应链竞争力，实现系统利润最大化。贾炜莹等运用博弈论和委托代理理论，研究在由一个经销商和多个制造商组成的简单供应链中，经销商如何进行供应链契约风险管理。戢守峰等研究了在由制造商、分销商和零售商组成的三级供应链中，需求不确定且与价格有关的条件下，收益共享契约对供应链的协调问题。

在收益共享契约模型的基础上，重点研究供给扰动下的生物质能供应链契约模型以及需求扰动下的生物质能供应链契约模型。首先研究无扰动下的生物质能供应链契约模型，运用模型计算出契约参数:分配系数和批发价格。在无扰动模型的基础上，进行供给扰动和需求扰动研究，得出在供给扰动和需求扰动下，供应链中分配系数和批发价格的波动，最后通过案例分析，验证结论。

1 无扰动下的生物质能供应链协调契约模型

1.1 基本假设

1）该模式的供应链结构是“公司＋基地＋农户”形式，农户生产原料，自行收集并使用农用车运输至基地，基地储存和保管原料，同时负责向公司稳定的生产地提供生产原料，最后将原料生产后出售至市场；

2）由于供应链实际运营中会面临原料缺货问题，公司作为供应链的主导，与基地之间签订收益共享契约，以鼓励基地向公司提供原料并向农户收集原料，作为原料采集基地，基地为了鼓励农户生产和提供原料，与农户签订收益共享契约；

3）基地仓储简化为EOQ模型，并且控制仓储周期小于原料腐烂变质时间；

4）假设市场需求为随机分布，其密度函数为f（x），分布函数为F（x），且F（x）单调递增，则有（Q为基地的存储量）；

5）假设该产品为供不应求的产品，即λ≥Q；

6）其他参数假设如下:cf为农户生产的单位成本，cc为公司生产成本，α为单位原料、单位时间的库存成本，w1为基地向农户的单位收购价，w2为公司向基地的单位收购价，Φ1为农户和基地之间的收益分配系数，Φ2为基地和公司之间的收益分配系数，λ为单位时间由基地运输至公司的原料数量，p为原料的市场价格。

1.2 供应链最优订购量

供应链利润为

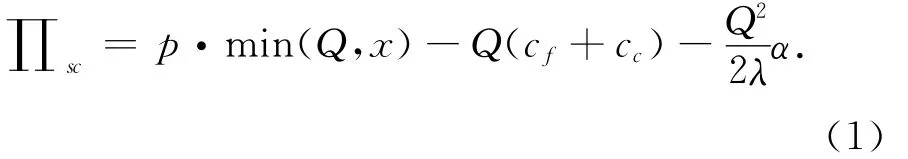
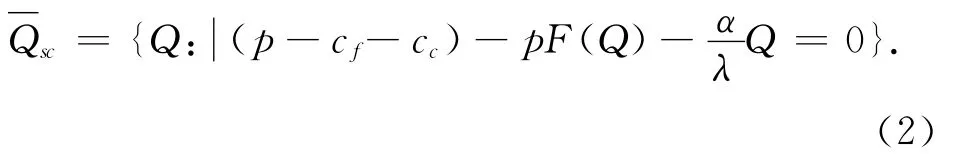
1.3 供应链契约协调

在收益共享契约的条件下，供应链各成员的收益函数

1）公司收益为

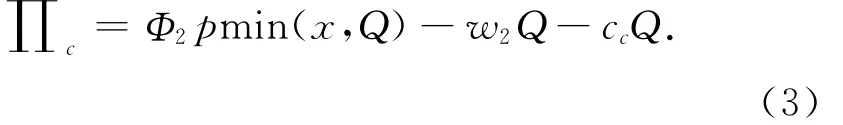
2）基地收益为

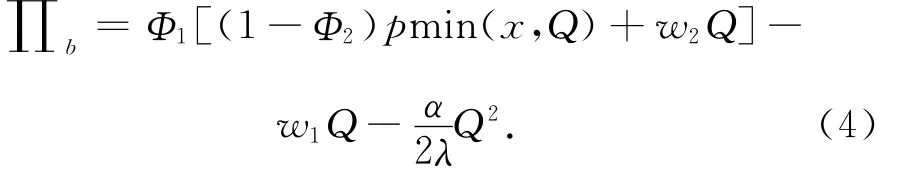
3）农户收益为

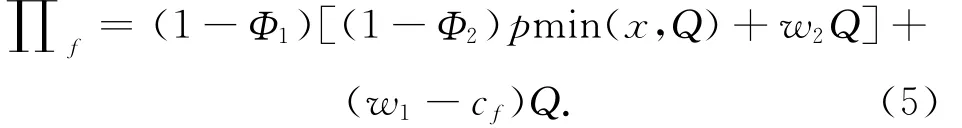
在收益共享决策下，根据公司利益最大化决定最优产量

得出公司最优订购量

在收益共享决策下，根据基地利益最大化决定最优产量

得出基地最优订购量

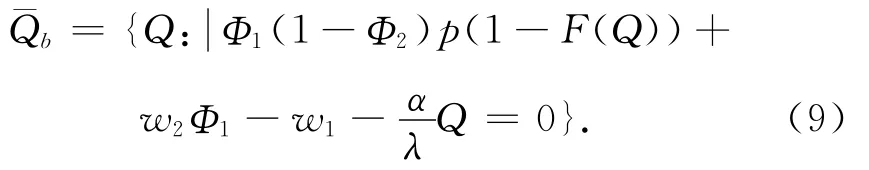
在收益共享决策下，根据农户利益最大化决定最优产量

得

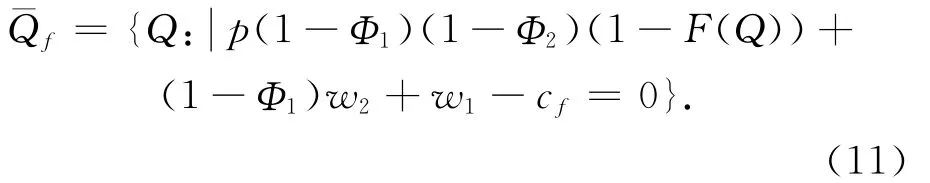
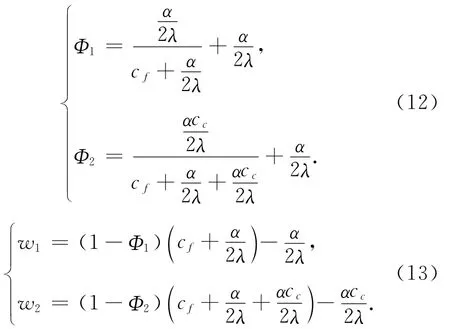
2 供给扰动下的生物质能供应链协调契约模型

2.1 基本假设

在前面的假设条件下，考虑供给扰动因素。供给扰动主要来源于供应链的下游，即农户方面，具体表现为供应链实际运营中受到的供给缺货扰动影响。假设供给扰动风险主要由公司承担，本模型中仅讨论库存缺货状态下的供应链契约协调。S为扰动的开始时间，T为扰动截止时间，D为扰动持续时间，D＝T－S。同时，假设扰动密度函数为g（t），扰动分布函数为G（t），单调递增。R为扰动分布函数的变化截止时间，即G（R－S）＝1。

2.2 最优订购量确定

在扰动函数影响下的单位时间库存成本为

因此，在n个订货周期中供应链利润为

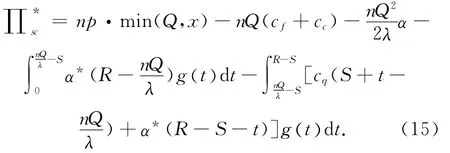
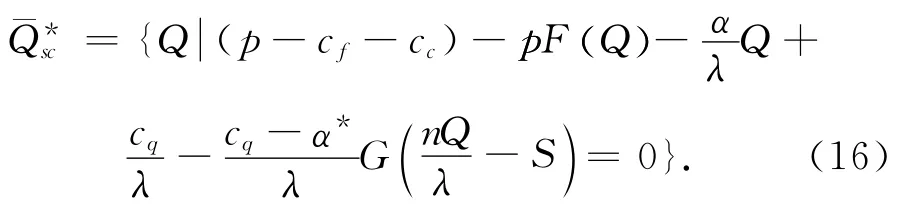
2.3 供应链契约协调

由于订购量增加，供应链契约参数产生变化。假设风险主要由公司承担，则供给扰动下对基地和农户的最优订购量不变，即¯Qf＝¯Qb＝¯Q＊sc，得出

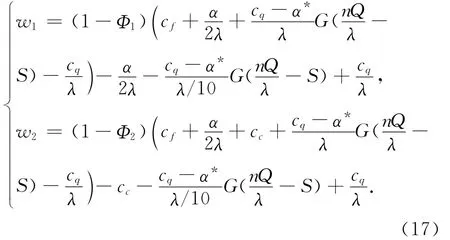
当收益共享系数不变，并且由公司承担缺货风险时，通过提高基地向农户和公司向基地的支付达到供应链协调，即w1，w2变大，以鼓励基地和农户提供更多的原料。

当基地和公司的支付价格不变，并且由公司承担缺货风险时，通过增加农户和基地的利润分成，即通过提高Φ1，Φ2鼓励农户和基地增加生产量和收购量，从而达到最优订购量。

3 需求扰动下的生物质能供应链协调契约模型

3.1 基本假设

在前面的假设条件下，考虑供给扰动因素。需求扰动从供应链终端出发，风险主要由公司和基地承担。主要考虑公司所面向的市场扰动，即市场需求量和价格的扰动。能源公司在销售过程中，可能会因为市场需求量的变动导致缺货，而造成销售损失，通常用失销成本来表示，l1为公司的单位失销成本。另一方面，在销售过程中，可能由于生产或者需求的变动，而导致原料多余或变质，多余原料的变质成本为l2。

3.2 供应链最优订购量

供应链利润为

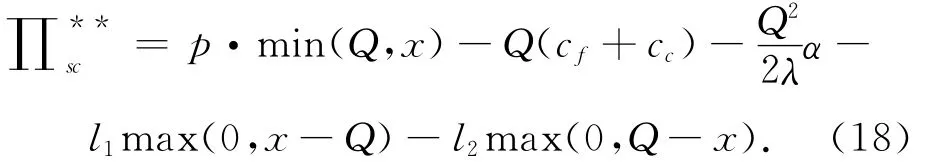
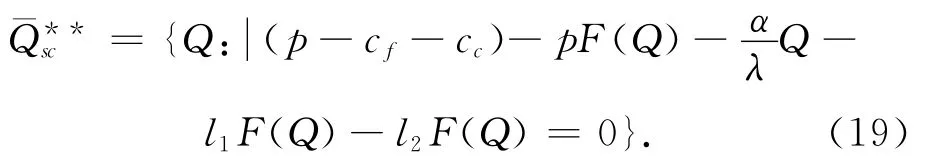
3.3 供应链契约协调

在收益共享的契约条件下，供应链各成员的收益函数为以下3个。

1）公司收益为

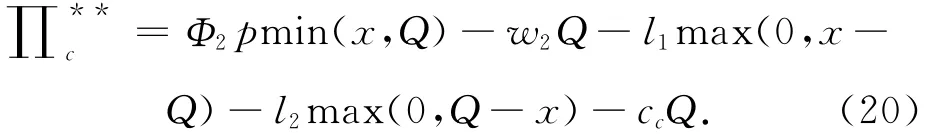
2）基地收益为

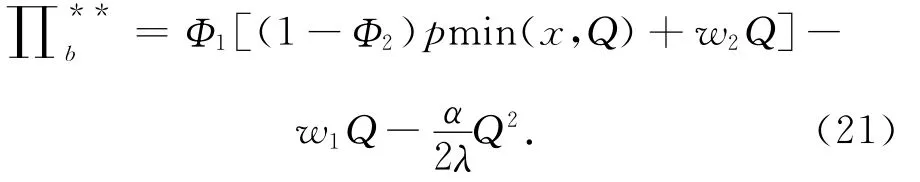
3）农户收益为

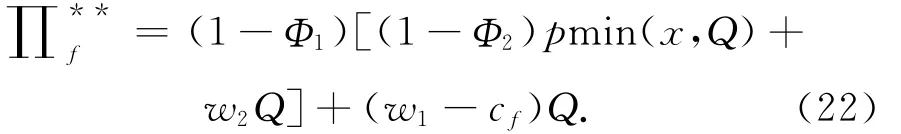
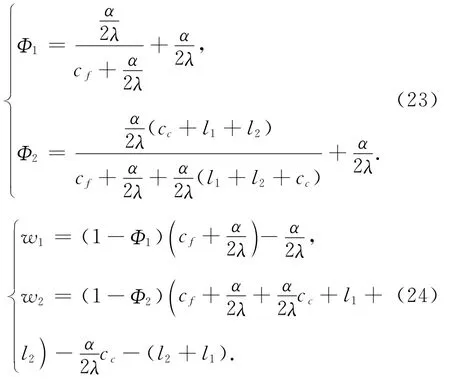
在考虑需求扰动时，可看出农户的销售价格同不考虑扰动时的价格一致，可得出扰动风险主要由基地和公司承担，与假设基本一致。由公司承担缺货和多余变质风险时，公司通过降低向基地的支付达到供应链协调，即w2变小。由于风险由基地和公司共同承担，对农户的收入没有影响，在收益共享契约机制下，农户提供给基地的批发价格小于其生产成本，作为回报得到基地销售收入份额的（1－Φ1），同时，基地也得到公司销售收入份额的 （1－Φ2）。

4 算例分析

根据目前的市场价格估量，对前文的模型参数做如下假设:cf＝2，p＝10，α＝1，cq＝0.5，λ＝20，cc＝0.5，l1＝0.5，l2＝0.5，同时，假设市场需求符合平均分布，市场容量为1 000，即

4.1 无扰动下的生物质能供应链协调分析

根据式（2）可求得无扰动下的最优订购量应为75.00；再根据式（10）得出分配系数Φ1＝0.037 35，Φ2＝0.031 13，w1＝1.924 4，w2＝1.961 6。

4.2 供给扰动下的生物质能供应链协调分析

在考虑到供给扰动时，此时的单位时间库存成本α＊为1.02。假设扰动函数为G（t）＝b＋t，b表示扰动大小，根据公式（16）可以得到扰动后的最优订购量，其中取S＝0，n＝1，则得出¯Q＊SC＝128.2＋可以看出在供应链受到供给扰动时，通过增加最优订购量来应对需求所带来的扰动，扰动越大，最优订购量也会随之越大，以应对库存周期中的供给扰动。

再根据式（17）得出

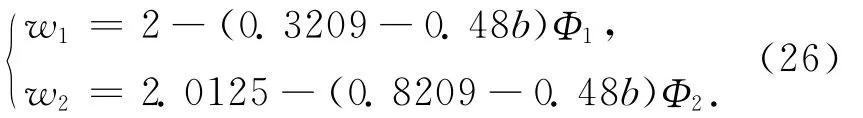
假设Φ1，Φ2不变时，w1，w2的取值为

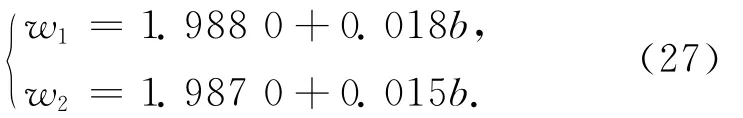
从式（27）可以看出，当收益共享系数不变，并且由公司承担缺货风险时，通过提高基地向农户和公司的支付达到供应链协调，即w1，w2变大，以鼓励基地和农户为公司提供更多的原料。当供给扰动增加时，w1，w2也会随之增加，以达到供应链协调的作用。

4.3 需求扰动下的生物质能供应链协调分析

在考虑到需求扰动时，根据式（19）求得此时的最优订购量为¯Q＊＊sc＝208.3。同时，根据式（23）可以得到Φ1＝0.0373 5，w1＝1.924 4保持不变，完全符合假设的结果，需求扰动只由基地和能源公司承担风险。根据公式（24）可以得到

从数据中可以看出，在考虑需求扰动时，农户的销售价格同不考虑扰动时的价格相同。由公司承担缺货和多余变质风险时，公司通过降低向基地的支付达到供应链协调，即w2变小。但可以看出Φ2有所增加，即能源公司通过降低批发价同时抬高分配系数，来分担其销售风险。

5 结 语

在生物质能供应链中，供给扰动和需求扰动会带给供应链较大的损失，因此，将重点研究供给扰动下的生物质能供应链契约模型，及需求扰动下的生物质能供应链契约模型。首先在收益共享契约模型的基础上，研究无扰动下的生物质能供应链契约模型，运用模型计算出契约参数、分配系数和批发价格。在无扰动模型的基础上，再进行供给扰动和需求扰动的研究。并通过模型计算得出以下结论:在供应链的供给扰动下，由公司承担缺货风险时，当收益共享系数不变，通过提高基地向农户、公司向基地的支付达到供应链协调，即w1，w2变大，以鼓励基地和农户提供更多的原料。在供应链需求扰动下，由公司承担缺货和多余变质风险时，公司通过降低向基地的支付，即w2变小，同时抬高分配系数Φ2来分担其销售风险，达到供应链协调。

［1］潘盛艺，张永，虞一峰，等基于交易成本的生物质供应物流组织结构比较分析研究［J］.物流技术，2010，29（1）:106－108.

［2］Lariviere M.Supply chain contracting and coordination with stochastic demand［C］.Quantitative Models for Supply Chain Management，Boston，1999（17）:233－268.

［3］Tsay A，Nahmias S，Agrawal N.Modeling supply chain contracts:a review［C］.Quantitative models for supply chain management，Boston，1999:197－232.

［4］朱美桦，王兴芳，韩瑛.基于模拟退火算法的供应链协调机制问题［J］.交通科技与经济，2013，15（3）:97－100.

［5］冯花平.基于多因素扰动的供应链应急协调研究［D］.北京:北京邮电大学，2008.

［6］贾炜莹，刘永胜，张剑.基于不对称信息的供应链契约风险管理［J］.商业研究，2011（1）:57－62.

［7］戢守峰，刘铭嘉，丁伟，等.基于三级供应链的收益共享契约协调研究［J］.东北大学学报，2008，29（11）:1652－1656.