数理统计模型对居民消费价格指数的应用研究

○李加兵 常 飞 田云飞

（云南大学工商管理与旅游管理学院 云南 昆明 650500）

一、引言

居民消费价格指数英文全称为Consumer Price Index，缩写为CPI，它是度量消费商品及服务项目价格水平随着时间变动的相对数，反映居民购买的商品及服务项目价格水平的变动趋势和变动程度。居民消费指数的变动率在一定程度上反映了通货膨胀或紧缩的程度，已成为宏观政策制定的重要依据之一。居民消费价格指数在整个国民经济价格体系中占有重要的地位，对于我国经济宏观调控具有正要的指导作用。另外，CPI的计算采用的是是固定权数按加权算术平均指数公式计算，CPI=（一组固定商品按当期价格计算的价值/一组固定商品按基期价格计算的价值）×100%。同时，居民消费价格指数还与经济通货膨胀有关，加深对居民消费价格指数的研究可以一定程度上抑制经济通货膨胀。有学者认为，当居民价格指数>3%就表示本地区已经发生了通货膨胀。居民价格消费指数是反应人们消费水平状况的重要指标，注重对居民的消费价格指数的研究可以增加政府对我国居民消费状况的了解，对我国政府的政策制定、经济宏观调控等都有重要的参考价值。

二、居民消费价格指数的时间序列分析

时间序列趋势图的方法在于是对我国目前居民消费价格指数（CPI）进行建模分析和预测，以达到合理预期和分析的目的。因为居民消费价格指数是一个反映居民家庭所购买的消费商品和服务价格水平变动情况的宏观经济指标。而时间序列分析是经济预测领域研究的重要工具之一。时间序列分为平稳性的与非平稳性的；居民消费指数具有非平稳性，但居民价格指数的非平稳性中又具有一定的季节性趋势。时间序列法是把CPI看成时序，建立A R MA或ARI MA进行预测，如张鸣芳等人应用x．12．ARI MA季节调整方法对上海市CPI序列进行季节调整、分析预测；神经网络法可以逼近任何非线性映射关系，从而求得问题的解答，如娄晶、赵黎明用神经网络中的B P网络建立了烟草类消费价格指数预测模型理论的研究动态表明，非数理统计的研究方法难以揭示居民消费价格指数二阶矩结构以外的结构信息，但是居民价格指数在实际数据中存在非线性结构数据。本文运用的数理统计模型有差分自回归移动平均模型、B P神经网络模型和以及参数拟合估计等。建模样本数据与测试样本数据为以2010年1月至2013年12月期间居民消费价格指数为实证数据。以下利用相应的数理统计模型对居民消费价格指数预测分析的过程：设时间序列为X（1），X（2），X（3），画出时间序列图如图1所示。

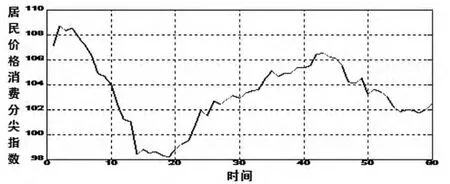
图1

居民消费价格指数的时间序列图显示的季节变动与时间数列的长期趋势大致成正相关时宜采用乘法原则。Y t=T t×S t×C t×I t。其中T t为长期趋势；S t为季节变动；C t为周期变动；I t为不规则变动。居民消费价格指数时间序列的相关性及平稳性检验。（1） 序列的相关性。由 Box．P i e r c e t e s t可得：X．s q u a r e d=l 966．917，d f=10，P-v a l u e<2．2 e-16。即拒绝原假设，由于Q统计量检验的原假设为不存在相关性，所以CPI序列存在相关性，可以对该序列进行A R MA建模。（2）平稳性检验。对CPI序列进行单位根检验得：D i c k e y．F u l l e r：1．8418，P-v a lu e=0．371，接受原假设，由于原假设为存在单位根，说明该序列不平稳。对其进行一阶差分后，经检验平稳。

三、数理统计模型应用研究与分析

第一，按月平均求出季节性趋势的居民消费价格指数为S（i），i=1，2，…12。

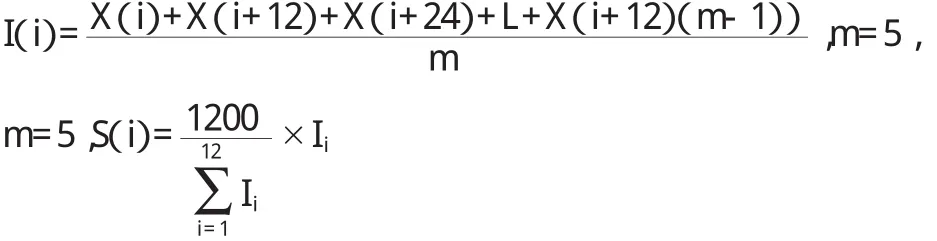
第二，运用差分自回归移动平均剔除长期趋势和周期变化，得到消费价格指数的周期项序列T Ct。经移动平均滤波对周期性影响有较好的抑制效果，如果移动幅度高，处理后的周期波动项会很少或者没有，即得到的指标是，由此可以求得居民消费价格指数的周期项序列进行一阶累加得到序列。

第四，运用差分自回归移动平均模型和B P神经网络数理分析进行实证数据拟合。首先，对实证数据进行预处理，变量为时间序列的平稳性检验是再分析处理的基础。检查C t平稳性的主要方法有散点图、单位根、非参数检验以及自相关函数。如果不能通过平稳性检验，那么就需利用差分法、对数法或者对数差分法将其转换为一个平稳序列。通过数理统计的A D F检验测试，结果表明所验证的时间序列具有良好的平稳性。最后是确定序列的阶数p，q，主要是用自相关图和偏自相关图观察序列的拖尾和截尾情况，在此基础上进行综合性判断，利用AIC、S I C值越小效果越佳的规则，得到p=1，q=8.其中AIC=-11.26508。

第五，由以上的分析可知，近期的居民价格消费指数的自相关和偏自相关两者均拖尾，因此可以考虑用ARI MA模型来拟合序列 CPI。综合考虑可以建立 ARI MA（1，1，1）、ARI MA（2，1，1）、ARI MA（1，1，2）、ARI MA（2，1，2）、A I L I MA（2，1，3）五个模型来对比各模型的拟合程度。

（1）ARI MA（1，1，1）模型下，对数似然函数值 LOG=-298.77，AIC=606.37，对残差作 Box-Ltest，得到 P=0.051318；

（2）ARI MA（2，1，1）模型下，对数似然函数值 LOG=-313.45，AIC=601.80，对残差作 Box-Ltest，得到 P=0.063372；

（3）ARI MA（1，1，2）模型下，对数似然函数值 LOG=-309.83，AIC=615.67，对残差作 Box-Ltest，得到 P=0.098134；

（4）ARI MA（2，1，2）模型下，对数似然函数值 LOG=-307.20，AIC=619.49，对残差作 Box-Ltest，得到 P=0.047317；

（5）ARI MA（2，1，3）模型下，对数似然函数值 LOG=-310.27，AIC=621.53，对残差作 Box-Ltest，得到 P=0.057924。

综上述模型均可以接受原假设，但p=2，q=1时AIC的值最小，残差的A C F也很快落入随机区间。所以根据AIC最小判定阶数的准则，因此，在研究分析时优先考虑选择ARI MA（2，1，1）模型。

四、预测拟合度的对比分析

预测拟合度效果的分析通常是采用平均绝对百分比误差和均方根误差这两项指标来进行对比：若均方根的值误差与平均绝对百分比的误差值越小，则说明预测效果越好。

表1

从表1可知，B P模型预测误差的R MS E和MA P E指标都比ARI MA模型的要小，相对而言B P预测效果更好。本文分别采用不同的数理统计模型对居民消费价格指数长期趋势项进行拟合，ARI MA和B P对周期项进行拟合，通过实证分析得出B P的拟合效果更好。

模型预测分析情况如下：根据ARI MA（2，1，2）模型对未来一年度的居民消费价格指数（2014.10-2015.10）进行预测，得到如 下值：96.80；96.44；97.63；97.06；98.38；98.15；98.74；99.13；100.35；100.28；99.94；98.51。鉴于同比指数和定基指数的定义，同时考虑到现实中的近期影响权重较大，以近24期（两年）的平均值作基准，换算后得相应预测值依次为：102.39；103.86；101.94；102.75；101.47；102.52；103.98；103.63；104.11；104.66；103.87；l 02.24。由此预测值可见，未来一年CPI的综合平均值为102.92，消费价格指数水平在平稳中稍有回落。

五、结论

以时间序列分析为基础的自回归分析模型在居民消费价格指数的预测中具有重要的应用。但由于居民消费价格指数很容易受到外界各种因子的干扰和冲击，利用A R MA模型进行的预测分析也更多的只是均值预测，并不能预测到潜在可能的指数变化或波动情况，这是用该模型预测的局限性。但整体预测分析的结果是具有重要的参考价值的。从本文的预测结果看，若无突发事件或是较大政策调整，未来一年内CPI的涨幅将维持在4.3%左右的平稳水平，且有下降的趋势。虽然CPI预测值属于并不精确的指标值，但其反应了价格变化的趋势，建议有关部门关注此趋势问题并进行相应的理论政策分析，同时做好国内外市场消费品的价格跟踪与分析工作，及时采用调控措施合理引导物价走势。关注价格趋势，加强利用统计模型手段进行预测分析和预警工作，切实做到未雨绸缪，有利于保持我国经济平稳快速发展的良好态势。

[1]张丽、牛惠芳：时间序列分析在居民消费价格指数预测中的应用[J].洛阳师范学院学报，2008（2）.

[2]国家统计局城市社会经济调查司：走近CPI[M].中国统计出版社，2010.

[3]郭海：基于月环比均值和翘尾因素的居民消费价格指数短期预测[J].统计与决策，2011（1）.

[4]陈玉海：我国CPI预测数量研究[D].长沙：中南大学，2009（7）.

[5]张健：SARIMA模型在预测中国CPI中的应用[EB/OL].http：//www.cnki.com.cn/Article/CJFDTotal-TJJC201105011.htm，2014-03-30.

[6]陈娟、余灼萍：我国居民消费价格指数的短期预测[J]．统计与决策，2004（4）．

[7]谢佳利、杨善朝、梁鑫：我国CPI时间序列预测模型的比较及实证检验[J]．统计与决策，2008（9）.