定量方法对比研究重复测量设计Bland-Altman一致限LoA的可信区间估计

南方医科大学南京临床医院（南京军区南京总医院医务部）（210002） 刘玉秀 缪华章 陆梦洁 陈 林

定量方法对比研究重复测量设计Bland-Altman一致限LoA的可信区间估计

南方医科大学南京临床医院（南京军区南京总医院医务部）（210002） 刘玉秀 缪华章 陆梦洁 陈 林

目的本文将介绍两种不同重复测量设计情形一致性评价的Bland-Altman一致限LoA及其可信区间估计方法，并探讨两种不同设计情形中分别涉及的两种不同可信区间估计方法的统计学性能，为方法学的选择应用提供理论依据。方法根据所测量样本真值是否变化，将重复测量设计分为两种类型，分别给出其Bland-Altman一致限LoA及其可信区间估计的两种方法（一种是Bland-Altman法，简称B-A法；另一种是方差估计反推法，简称MOVER法），借助Monte-Carlo模拟技术，在正态分布假定下，设定不同的样本量、不同的个体内变异性，分别采用B-A法和MOVER法，模拟获得95%LoA范围的95%可信区间对总体设定的覆盖率，用覆盖率与95%的接近程度评价不同方法的统计学性能，理论上该覆盖率与95%越接近，反映方法的统计学性能越好。结果用B-A法估计LoA可信区间的覆盖率随样本量的增大而增大，样本量为20以下时覆盖率不足90%，即使在样本量达到250时，其覆盖率仍在94%以下，而MOVER法覆盖率始终紧紧围绕事先设定的可信度95%微小波动，甚至在样本量为10时覆盖率也能接近95%。结论MOVER法用于方法对比研究重复测量设计的LoA可信区间估计具有很好的统计学性能。

方法对比研究 重复测量 Bland-Altman法 一致限 可信区间 MOVER法

医学研究中常常会遇到两种测量方法对比研究的一致性评价问题。就两种测量方法对同一样本各测量一次的设计情形，进行一致性评价的统计学方法可考虑使用Bland和Altman提出的一致限（lim its of agreement，LoA）方法［1］，通过计算两种方法结果间差异的均数及其标准差获得LoA，根据其是否在可接受的误差范围内来判定两测量方法间的一致性。目前，应用Bland-A ltman一致限LoA进行方法对比研究的一致性评价得到普遍认可［2］，但有两方面的问题并未引起足够的重视。第一个问题是，LoA在概念上只能属于统计描述的范畴，反映的是所测量样本特征，并未涉及对总体的推断，会误导一致性的评价，甚至得出错误的结论。正是由于这一极其重要并带有普遍性的问题，引起不少学者的注意，强烈呼吁要进行一致性的正确评价，必须考虑样本抽样误差的问题［3-5］。甚至有学者指出，LoA不能作为一致性判定的限值，其可信区间的限值才是真正的一致性限值［5］。第二个问题是，在方法对比研究中，即使采用了重复测量设计，但未能很好地按照重复测量机制应用Bland-Altman法进行一致性评价，甚至还存在方法学上的错误［6］。

本文将对方法对比研究重复测量设计两种不同情形一致性评价的Bland-Altman一致性限值LoA及其可信区间估计方法进行介绍，并通过对两种不同设计情形中分别涉及的两种不同可信区间估计方法的Monte-Carlo模拟实验，评价其统计学性能，为方法学的选择应用提供理论依据。

样本真值即时变化的重复测量设计情形

Bland和Altman曾多次引用Bow ling提供的数据作为例子［7-8］。测量心排量的两种方法分别是阻抗心动描记术（impedance cardiography，IC）和放射性核素心室显像术（radionuclide ventriculgrraphy，RV），RV是一种侵入性的方法，而IC是非侵入性的，为了评价测量心排量两种方法的一致性，以考察IC方法是否可以替代RV方法，研究者测量了12例病人，不同的病人用两种方法分别进行了3～6次测量。

基于通用性考虑，以x和y分别代表RV和IC测量方法，n为病人例数，令mxi和myi分别代表测量次数（i＝1，2，…，n），xij代表RV方法第i例病人的第j次测量结果（j＝1，2，…，mxi），yij代表IC方法第i例病人的第j次测量结果（j＝1，2，…，myi）。由于两方法结果成对出现，则mxi＝myi＝mi。LoA估计基于每对结果差值进行，记dij为第i例病人用两种测量方法的第j次测量结果差值，dij＝xij-yij，对dij建立单因素的随机效应模型（one-way random effectsmodel）为

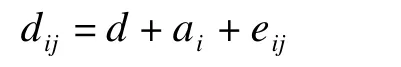
其中，d是两种方法的真实差值，ai和eij为相互独立的均数为0、方差分别为的正态分布变量。一致限可定义为两方法真实差值、个体间和个体内随机变异的和。

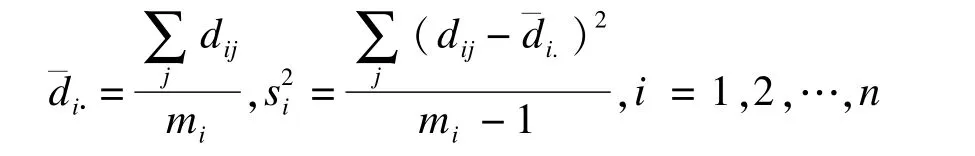
其期望值为

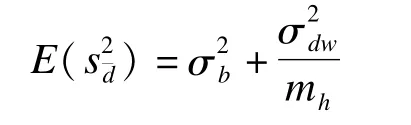
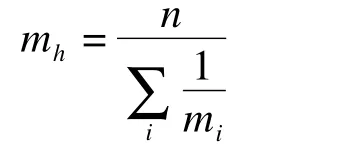
则100（1-β）%LoA的限值估计分别为

为了获得上述LoA两个限值的可信区间，按照常规的可信区间估计方法获得各限值的标准误估计。经数理统计研究，该标准误的平方计算公式为

则计算LoA下限的100（1-α）%可信区间的公式为

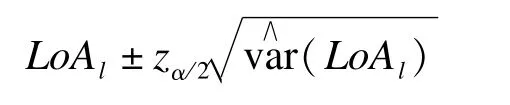
zα/2为标准正态分布的100（1-α/2）%分位数。同理，计算LoA上限的100（1-α）%可信区间的公式为

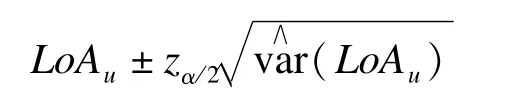
以上是用Bland-Altman法计算的可信区间，可见Bland-Altman法可信区间估计值对参数的点估计值具有对称性。但是，由于LoA的两个限值是正态分布均数和方差的组合量函数，根据均数和方差的统计学性质，均数的抽样分布仍服从正态分布，但方差的抽样分布并不服从正态分布，因此通过均数和方差合成而获得的LoA的两个限值其分布在理论上并不服从正态分布。Bland-Altman法强行进行对称处理所计算的可信区间其统计学性能值得怀疑。Efron和Tibshanri认为，将偏态分布统计量强行对称化进行可信区间估计是“最严重的错误”［9］。

为此，基于Zou和Donner提出的方差估计反推法（themethod of variance of estimates recovery，简称为MOVER法）［10-11］，两个参数之和或之差的可信区间估计，均可根据两个参数各自的可信区间限值而获得的原理，Zou导出了LoA的可信区间估计方法［12］，100（1-β）%LoA的下限LoAl的100（1-α）%可信区间下限和上限的计算公式分别为LoAl-LME和LoAl＋RME。同理，100（1-β）%LoA的上限的100（1-α）%可信区间下限和上限的计算公式分别为LoAu-RME和LoAu＋LME。其中

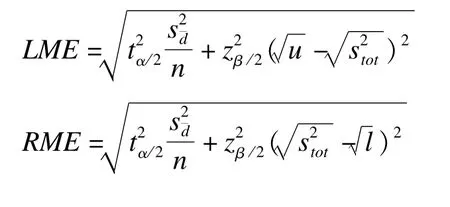
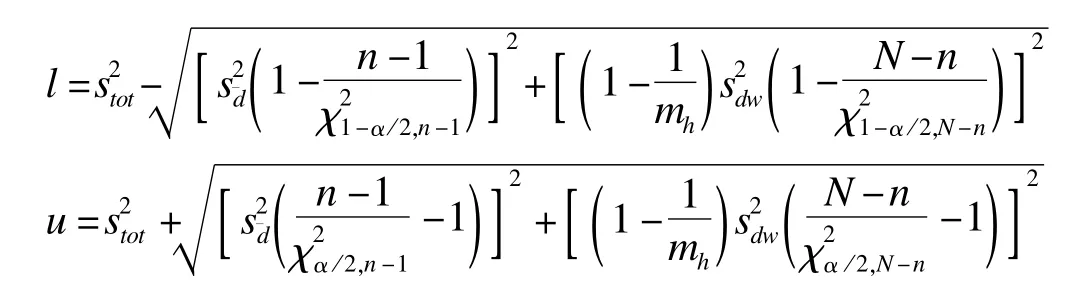
样本真值相对不变的重复测量设计情形

在方法对比研究中，当样本中欲测定的指标真值恒定或者在一定时间内相对不变时，例如颈动脉狭窄程度、影像载体上的病变大小、血标本中的某指标含量等，用两种方法进行多次测量，并不需要像真值结果具有随时变化特性时那样，必须保证两方法测定同时进行、结果成对出现，两种方法对同一样本的测量次数可以不同，即不必要求mxi＝myi。对两方法的测量结果xij和yij分别建立单因素的随机效应模型

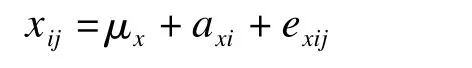
式中μx为x的真值，axi和exij为服从均数为0、方差分别为的正态分布变量。

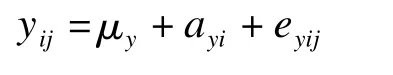
式中μy为y的真值，ayi和eyij为服从均数为0、方差分别为的正态分布变量。

为了对LoA及其可信区间进行估计，分别计算出各个体x和y的均数和方差计算个体内随机误差的合并方差估计值

计算每一个体两种方法的均数差值

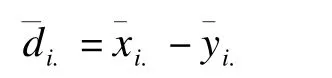
则两种方法均差的均数及其方差分别为

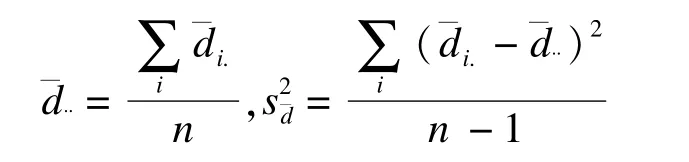
根据Bland和Altman的方法，100（1-β）%LoA的限值估计分别为

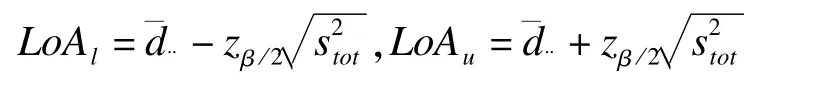
为了获得上述LoA两个限值的可信区间，按照Bland-Altman法，获得各限值的方差估计

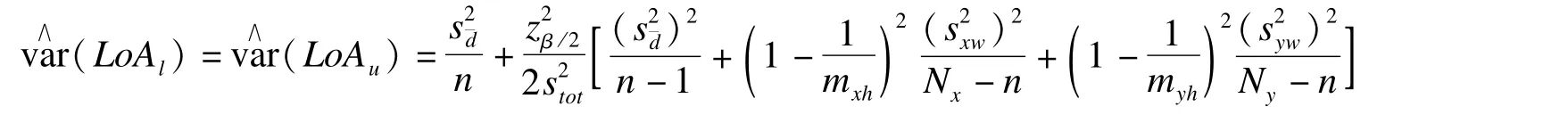
有关100（1-β）%LoA的两个限值的100（1-α）%可信区间估计采用MOVER法的计算公式与前面介绍的完全相同，只是计算可信区间公式中涉及到的l和u需按下式求算

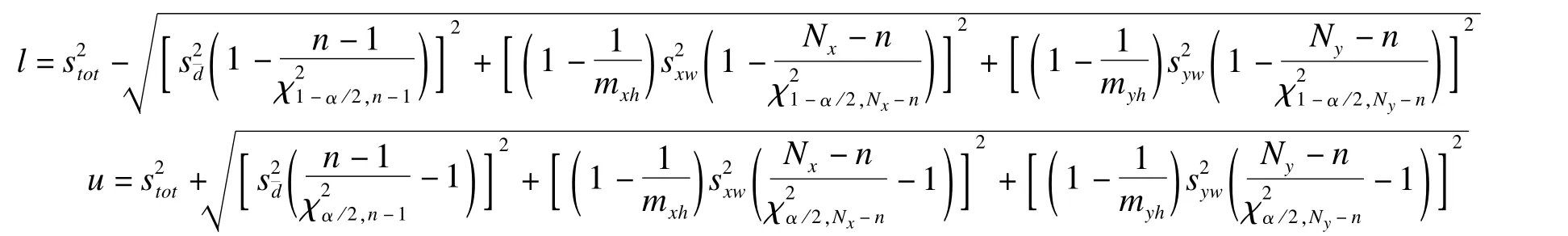
M onte-Carlo模拟实验

在模拟研究之前，首先对前面用RV和IC两种方法重复测量12例病人心排量结果的例子进行分析。此例本为样本真值即时变化的重复测量设计，为节省篇幅，这里也作为样本真值相对不变的重复测量设计分析的例子，结果显示，两种方法的均差为0.71，表明IC方法测量结果较RV方法平均低0.71，按真值结果是变化的情形考虑，两方法95%一致限LoA为（-1.30，2.72），按照BA法计算的95%LoA范围的95%可信区间为（-2.61，3.63），按MOVER法计算的可信区间为（-2.66，4.08）。如果按真值结果是不变的情形考虑，两方法95%一致限LoA为（-1.35，2.77），按照BA法计算的95%LoA范围的95%可信区间为（-2.35，3.67），按MOVER法计算的可信区间为（-2.70， 4.12）。鉴于本例只有12例病人，累计测量次数也仅有60次，所求算的LoA可信区间结果（MOVER法）下限为-2.66，上限达到4.08，与临床能够允许的误差限值相比似乎偏大，尚不足以得出两方法具有一致性的结论，这与原研究者Bow ling认为IC测量与RV测量间缺少一致性的结论一致。

为了考察上述可信区间估计的统计学性能，针对两种不同重复测量设计类型，基于测量结果服从正态分布，分别设定不同的样本量和不同的个体间变异占总变异的比例（个体间方差比例），进行Monte-Carlo模拟实验。本文随机模拟实验借助SAS 9.2系统编程实现。

对于真值变化的重复测量设计情形，在不同的样本量和重复测量次数设定下，按照两种方法测量结果差值的总体均数为0，个体间方差为个体内方差为产生第i例个体的第j次测量结果即dij。具体步骤为，先按个体例数产生服从分布的随机数，然后针对不同个体再产生与个体内重复测量次数对应的服从分布的随机数，最后对两个随机数变量求和即可。如果限定则产生的dij是一服从标准正态分布N（0，1）的随机数变量。随机模拟产生足够多的随机变量，分别计算95%LoA范围的95%可信区间，如果可信区间估计方法统计学性能优良，则根据正态分布特点，计算出的可信区间理论上将会有95%的比例覆盖-1.96到1.96范围因此，我们采用覆盖率来评价可信区间估计方法的统计学性能，模拟实验的覆盖率愈接近95%，表明所用的可信区间估计方法统计学性能愈好。为了尽量模拟实际中的不同情形，我们将样本量设定为10、20、50、100、150、200、250共7种情形，个体间方差比例从0.5开始，每次增加0.1，直至0.9，共5种情形（该比例小于0.5时表明个体内变异大于个体间变异，显然对一致性评价不具有实际意义），统一设定每例的重复测量次数为5次，每一组合的模拟次数为10000次。模拟结果见表1。

对于真值不变的重复测量设计情形，需要对两种测量方法分别产生随机数变量。随机变量xij来自于两个均数为0，个体间方差和个体内方差分别为的随机变量之和，限定同理yij随机变量来自于两个均数为0，个体间方差和个体内方差分别为的随机变量之和，限定计算95%LoA范围的95%可信区间，根据正态分布特点，模拟实验次数足够多时，计算出的可信区间理论上将会有95%的比例覆盖范围按照真值变化的重复测量设计情形给定模拟参数组合，x和y变量的重复测量次数分别设为5次和4次。模拟结果见表1和图1。

可见，Bland-Altman法LoA可信区间估计方法在样本例数较小时覆盖率偏低，而MOVER法甚至在样本例数仅为10时，也较为接近95%，表明采用MOVER法进行LoA范围可信区间估计具有很好的可靠性，是一种较为理想的LoA范围可信区间估计方法。

讨 论

尽管Bland和A ltman给出了针对重复测量设计的LoA可信区间估计方法［7-8］，但研究表明，在小样本量时该方法达不到应有的统计学性能。而本文介绍的重复测量设计LoA可信区间估计的新方法即MOVER法，经Monte-Carlo模拟实验表明，甚至在小样本量时仍然具有优良的统计学性能。不仅如此，该方法无论是在两种重复测量设计的哪一种情形下，都不要求个体重复测量次数相等，具有相当的灵活性和实用性［12］。另外，尽管MOVER法的计算过程貌似复杂，但从其推导和构建过程可见，除一般的统计运算外，也只是涉及到正态分布和卡方分布的分位数，这在方法学实现上并不困难。因此，MOVER法是一种值得推荐用于方法对比研究重复测量设计的LoA可信区间估计方法。

表1 方法对比研究重复测量设计两种不同情形分别采用两种不同的方法进行95%LoA范围的95%可信区间估计覆盖率（%）的模拟结果（模拟次数为10000次）

当然，本文模拟是在假定测量结果服从正态分布的前提下进行的，对于不同的重复测量次数包括个体重复测量次数不同的情形，我们另外进行了模拟，结果显示各方法的统计学性能具有类似的特点和规律，鉴于篇幅这里未予列举。至于重复测量设计Bland-Altman法一致性评价的应用条件考察，可参照单样本两种测量方法仅测量一次的情形，通过图示方法，例如绘制Bland-Altman图和差值的直方图，粗略判定两种测量方法结果及其差值是否服从正态分布、在测量范围内差值的变异是否随测量结果变化而变化等。对于不能满足Bland-Altman法应用条件即数据行为不良的重复测量设计的一致性评价，还需进一步的方法学探讨。

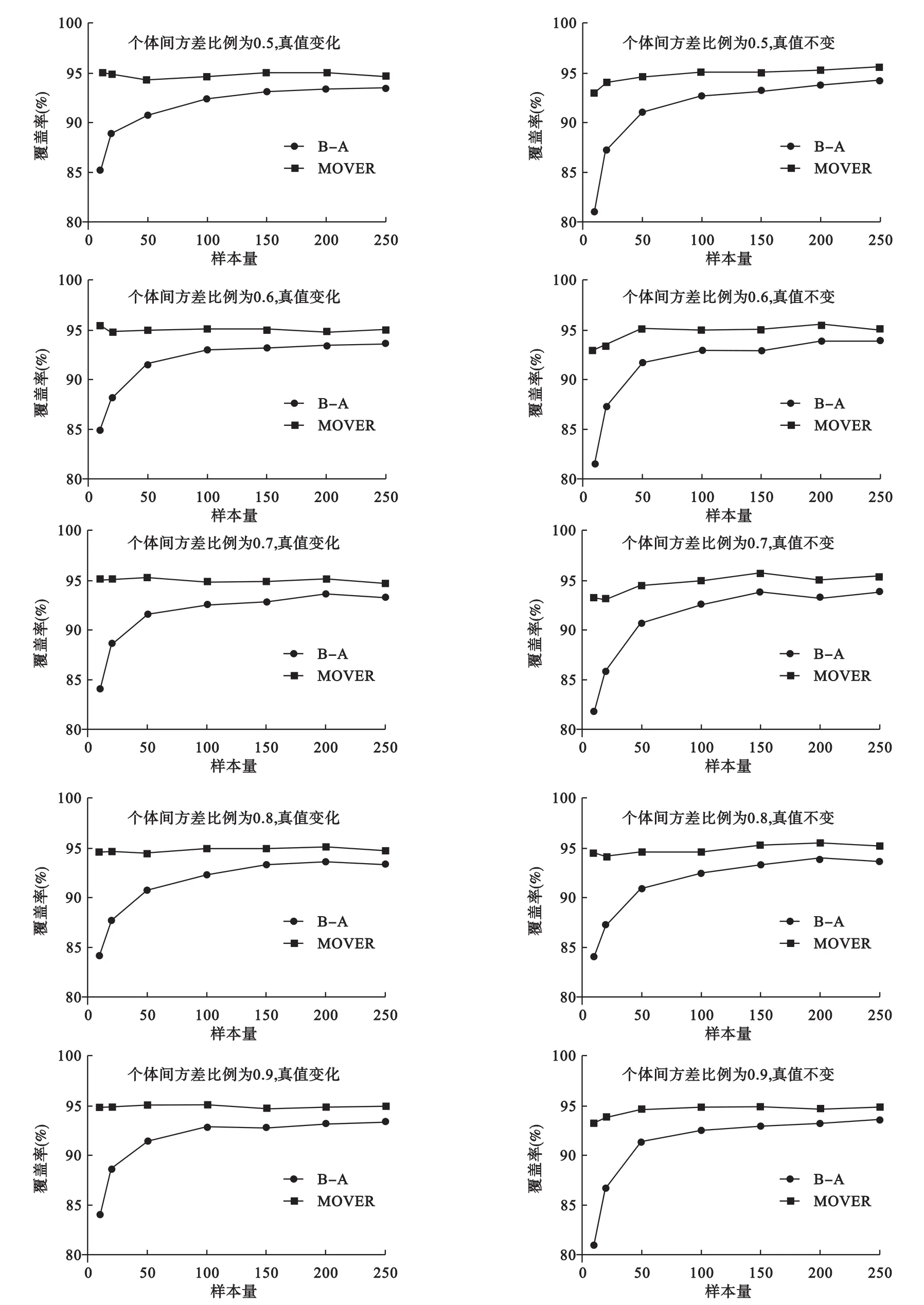
图1 方法对比研究重复测量设计两种不同情形分别采用两种不同的方法进行95%LoA范围的95%可信区间估计覆盖率（%）模拟结果（模拟次数为10000次）

国内目前对采用Bland-Altman法评价一致性的研究仅局限于简单的方法学介绍，也仅限于两种测量方法单次测量的情形，对LoA范围可信区间估计更是较少深入涉及，尚未见到有关重复测量设计的方法学介绍［13-17］，这需要我国的方法学研究者和应用者，无论从理论研究和实际应用都应给予高度关注。

1.Bland JM，Altman DG.Statisticalmethods for assessing agreement between two methods of clinicalmeasurement.Lancet，1986，1（8476）：307-310.

2.Zaki R，Bulgiba A，Ismail R，etal.Statisticalmethods used to test for agreement of medical instruments measuring continuous variables in method comparison studies：a systematic review.PloS ONE，2012，7（5）：e37908.doi：10.1371/journal.pone.0037908.

3.Hamilton C，Stamey J.Using Bland-Altman to assess agreement between twomedical devices-don＇t forget the confidence intervals！JClin Monit Comput，2007，21（6）：331-333.

4.Ham ilton C，Lew is S.The importance of using the correctbounds on the Bland-Altman lim its of agreement when multiplemeasurements are recorded per patient.JClin Monit Comput，2010，24（3）：173-175.

5.Stockl D，Cabaleiro DR，Uytfanghe KV，et al.Interpreting method comparison studies by use of the Bland-Altman plot：reflecting the importance of sample size by incorporating confidence lim its and predefined error limits in the graphic.Clin Chem，2004，50（11）：2216-2218.

6.Myles PS，Cui J.Using the Bland-Altmanmethod tomeasure agreement w ith repeated measures.Br JAnaesth，2007，99（3）：309-311.

7.Bland JM，Altman DG.Measuring agreement in method comparison studies.Stat MethodsMed Res，1999，8（2）：135-160.

8.Bland JM，Altman DG.Agreement between methods of measurement with multiple observations per individual.J Biopharm Stat，2007，17（4）：571-582.

9.Efron B，Tibshirani RJ.An introduction to the bootstrap.New York：Chapman＆Hall/CRC Press，1993.

10.Zou GY，Donner A.Construction of confidence lim its about effect measures：a general approach.StatMed，2008，27（10）：1693-1702.

11.Donner A，Zou GY.Closed-form confidence intervals for functions of the normalmean and standard deviation.Stat Methods Med Res，2010，21（4）：347-359.

12.Zou GY.Confidence interval estimation for the Bland-Altman lim its of agreementw ith multiple observations per individual.Stat Methods Med Res，2013，22（6）：630-642.

13.李镒冲，李晓松.两种测量方法定量测量结果的一致性评价.现代预防医学，2007，34（17）：3263-3266.

14.陈卉.Bland-Altman分析在临床测量方法一致性评价中的应用.中国卫生统计，2007，24（3）：308-309.

15.周宇豪，许金芳，贺佳.诊断试验一致性评价中几种方法的比较与应用.中国卫生统计，2011，28（1）：40-42.

16.萨建，刘桂芬.定量测量结果的一致性评价及Bland-Altman法的应用.中国卫生统计，2011，28（4）：409-411.

17.缪华章，陈林，刘玉秀.定量方法对比研究一致性评价Bland-Altman法LoA的可信区间估计.中国卫生统计，2014，31（1）：64-67.

（责任编辑：郭海强）

Confidence Interval Estimation for the Bland-Altman Lim its of Agreement w ith Repeated M easurements in Quantitative M ethod Com parison Studies

Liu Yuxiu，M iao Huazhang，Lu Mengjie，et al（Nanjing General Hospital of Nanjing Military Command，Southern Medical University（210002），Nanjing）

ObjectiveThis paper w ill introduce agreement evaluation by using the Bland-Altman LoA and is confidence interval estimatemethod in two different repeated measurement design scenarios，and explores the statistical performance of two different confidence intervalestimationmethods in each scenario，and provides a theoreticalbasis for the selection and application of themethodology.MethodsAccording to themeasured sample true value whether changed，the repeated measurement design is divided into two types，and gives the Bland-Altman LoA w ith its two confidence interval confidence interval estimatemethods（one is Bland-Altman method，another is the MOVER method），respectively.By using Monte-Carlo simulation technique，set the different sample sizes and individual variability under the assumption of the normal distribution，and obtain the coverage rates of the B-A and MOVERmethodswhich be used to simulate the 95%confidence interval of the 95%LoA for the population.The adjacency degree between the coverage rates and 95%can be used for evaluating the statistical performance，theoretically，the coverage ratesmore close to 95%，reflect the statistical performance of themethod ismuch higher.ResultsThe coverage rate of LoA confidence interval estimation by using the B-A method is increasesw ith the sample size，but less than 90%when the sample sizewas under20，and still below 94%even when the sample size is250，while the MOVERmethod coverage closely around the small fluctuations in the credibility of 95%predefined，it can close to 95%even when sample size is 10.ConclusionThe confidence interval estimation for LoA by using MOVER method in method comparison studies w ith repeated measurements design works well and deserves recommendation.

Method comparison study；Repeatedmeasurements；Bland-Altmanmethod；Lim its of agreement；Confidence intervals；MOVER