数学模型在HPV疫苗经济学评估中的研究进展*

方 亚宋晓彬周 鼒赵勤俭

数学模型在HPV疫苗经济学评估中的研究进展*

方 亚1，2，3△宋晓彬2，3，4周 鼒1，2，3赵勤俭1，3，5

人乳头状瘤病毒（human papilloma virus，HPV）持续感染引起宫颈癌、肛门癌和生殖器疣等多种HPV相关疾病。其中，宫颈癌和生殖器疣已严重威胁到人群的生命健康［1-6］，其防治工作成为当前亟待解决的公共卫生问题。预防性HPV疫苗已经被证明可以有效阻断HPV感染和降低人群宫颈癌和生殖器疣发病率，并且其已在多个国家获得了使用许可［4］。

HPV疫苗接种方案的经济学评估对科学规划HPV疫苗接种方案和优化卫生资源配置有着重要作用。因宫颈癌等HPV相关疾病进展缓慢，接种HPV疫苗的收益要经过数十年才能显现［7］，故研究者通常采用基于HPV相关疾病自然史的数学模型模拟预测干预效果和终生成本［8-9］。2000年，美国医学研究院开始采用数学模型对HPV疫苗进行经济学评估［10］，此后，采用该方法对HPV疫苗进行经济学评估的文献逐渐增多，但是其数学模型的构建方法和结构各有千秋。

本文拟对2000年以来发表的该类研究中的数学模型进行模型结构、关键参数和研究结论等比较，最后对各类模型的特点及目前研究中存在的问题进行探讨，为后续研究提供借鉴。

数学模型

应用于HPV疫苗经济学评估的数学模型主要基于宫颈癌等HPV相关疾病自然史［11］。疾病自然史指在没有医药干预的情况下疾病的演变进程［12］，如图1为宫颈癌疾病自然史流程图。评估中的数学模型可以从多个角度进行分类，如按照是否随机分类、按照队列的特点分类、按照事件连续性分类等。本文根据模型中感染力（易感者感染HPV的可能性）是否与HPV流行率有关，将HPV疫苗经济学评估中的数学模型分为3类，即静态模型（static model）、动力学模型（dynam ic model）和混合模型（hybrid model）［6］。

图1 宫颈癌的疾病自然史

其中，静态模型的结构可以用图2（A）示意，动态模型用图2（B）示意。图中的各仓室代表不同健康状态［13］，易感表示人群对HPV易感，感染HPV表示已经感染HPV但尚未发病，CIN表示患者已形成宫颈上皮内瘤变，宫颈癌表示患者已经进入宫颈癌期。图2中Pi和希腊字母为概率和函数的符号，表示不同健康状态间的转变情况。而混合模型联合使用两类模型，其模型结构是图2（A）和（B）的复合。在经济学评估中，通过改变模型结构和参数来预测不同接种方案的影响，如加入筛查和治疗仓室对各概率进行修正，预测筛查和治疗方案的影响。

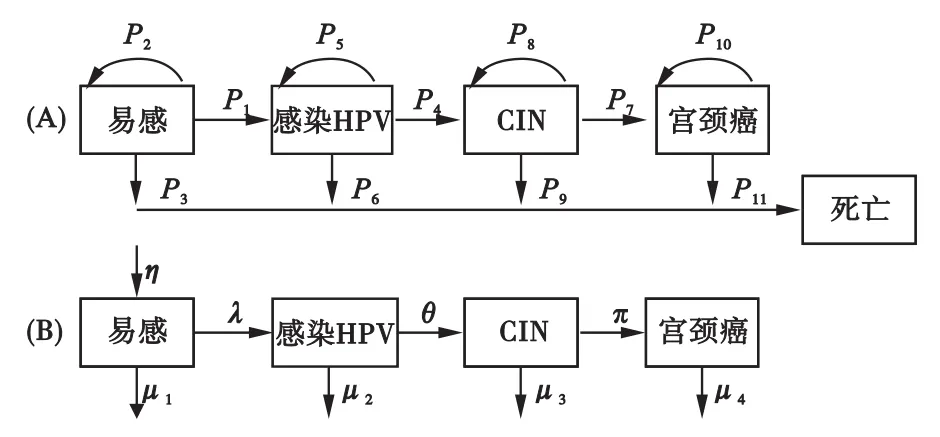
图2 静态模型和动力学模型的流程图

静态模型

静态模型模拟特定队列（如12岁女性）人群的期望寿命［13］。静态模型是一类典型的线性概率模型，追踪易感队列在整个发病过程中所经历的仓室。队列中的个体按照事先确定的概率从一个仓室进入另一个仓室，并且转变概率Pi（图2（A）中的P1到P9）通常不随时间改变。静态模型通常仅对单个“封闭”队列进行模拟，即模拟过程中无新个体进入，若个体全部死亡则模拟结束［8］，它包括马尔科夫模型、蒙特卡洛模型、基于发病率的模型等。

马尔科夫模型基于疾病发展过程的马尔科夫性，将疾病分为不同状态，并根据各状态间转移的概率模拟疾病的发展过程。2003年，Sander为了综合评估HPV疫苗的效果和成本效益，构建了与图2（B）结构一致的马尔科夫模型［14］。研究发现，与仅对患病人群进行治疗相比，使用疫苗具有成本效益，且疫苗有效性对成本效益影响最大。基于此模型，Kulasingam等学者进一步将感染仓室分为高危型和低危型，CIN仓室分为CIN1和CIN2/3仓室，宫颈癌仓室分为Ⅰ到Ⅳ四个仓室［15］。研究发现，在接种疫苗的情况下，宫颈癌筛查仍是必须的，但是可适当延长筛查的间隔时间；另外，接种年龄、疫苗覆盖的亚型、有效性及持续时间对经济评估结果影响较大。Goldie进一步细化模型，将感染仓室分为：①HPV16和18型持续感染；②其他高危型持续感染；③低危型持续感染；④短暂感染［16］。在Goldie的研究基础上，Kulasingam发现在计算人群免疫的情况下单独对12岁女孩进行接种更加具有成本效益［17］。Kohli和Rogoza分别研究了已建立筛查机制的国家引入HPV疫苗的问题，研究认为在这些国家使用疫苗仍然具有成本效益［18-19］。2010年，Kim在探讨是否将男同性恋人群纳入免疫计划时，构建包含肛门癌和生殖器疣的模型［20］，发现12岁、20岁和26岁接种疫苗都具有成本效益，但12岁接种成本效益最高，而且肛门癌发病率、疫苗持续时间和HIV流行率对结果影响较大。

事实上，宫颈癌等疾病仅具有半马尔科夫性，即病人长期处于某特定健康状态会对疾病的发展产生影响。因此，Bergeron、Coupe和Thiry等在马尔科夫模型中引入不同时间间隔的状态转移率［21-23］，以更加真实地模拟疾病发展过程。

马尔科夫性问题在一定程度上得到解决，但个体随机性问题仍然存在，因此，蒙特卡洛法被引入到马尔科夫模型中形成蒙特卡洛模型。蒙特卡洛模型追踪每个个体的临床路径，是随机模型的一种，可以解决多个不确定性参数间相互影响的问题，更加真实地刻画疾病进展的随机性。Van de Velde为测定四价HPV疫苗的影响，构建包含7个健康状态的鳞状细胞癌自然史模型，每个健康状态又包含10个表示感染和免疫状态的仓室［24］。该模型考虑到HPV16或18与其他亚型病毒间的重叠感染。2007年，Kim等学者构建了包含39种HPV亚型的数学模型［25］，获得了不同亚型感染后的健康状态转移概率和主动免疫概率等参数，此后，该模型被众多学者应用于HPV疫苗经济学评估。

此外，Law rence和Chesson构建了HPV相关疾病基于发病率的模型［10，26-27］。Chesson发现，在考虑男性患病情况下，若女性的疫苗覆盖率很低（如20%），将男性加入免疫计划可以显著提高成本效益，但提高女性的覆盖率更具成本效益［26-27］。

静态模型假设感染力为常数，并且模拟的是封闭队列，因此，不能测算群体免疫效应。为解决此问题，Vanagas尝试构建了“开放”静态模型［28］，但使用这一模型的文献较少。

动力学模型

动力学模型模拟整个人群随着时间变化的发病情况［13］。动力学模型通常以常微分或偏微分方程组表示，是一类典型的非线性确定性模型［29］。与静态模型最为重要的区别是，动力学模型中表示健康状态间转变的函数随着时间而变化［13］，它刻画病毒通过性行为传播的过程，其病毒感染力是感染人数、性行为模式等诸多变量的函数［11］，所以动力学模型能够测算性行为在HPV传播中的作用，弥补了静态模型忽略群体免疫效应的问题［7］，这就使得模型更加贴近现实。此外，它所追踪的不是静态队列，而是随着时间不停改变的队列，人群不断以参数η的速度进入队列，并且以参数μ的速度离开队列。所以，动力学模型可以预测疾病的长期发展状态，避免了静态模型中因人口死亡导致模拟提前终止的问题。

2002年，Hughes为了研究性行为和疫苗对人群HPV感染率的影响，提出了人群中HPV感染力函数和性行为活动函数［30］。研究表明，人群特点（性伴混合模式、性伴更换频率）和疫苗特性对HPV流行起到至为关键的作用，男女两性均接种疫苗能够最大程度降低HPV的流行率；此外，在疫苗保护作用为10年的条件下，仅对高危人群进行干预是不够的，应当扩大到普通人群；由于存在替代效用，覆盖更多亚型的疫苗能更有效地降低宫颈癌的患病率。Hughes的研究给了其他学者很多有益提示。

2003年，Barnabas和Garnett探讨了未建立筛查机制的发展中国家引入HPV疫苗后对人群的影响［31］。研究者分别针对男性与女性建立了两个不同的偏微分方程组模型。其中，男性模型分为易感人群、接种和感染3个仓室；女性模型分为易感、接种、感染、低度鳞状上皮内病变、高度鳞状上皮内病变、宫颈癌和癌症存活者7个仓室。研究表明若希望宫颈癌患病率下降80%，则疫苗的覆盖率至少要达到66%；同时，要明显观察到癌前损伤和癌症患病率的下降至少分别需要40年和60年。2006年，Barnabas为了研究在芬兰引入HPV16型疫苗后性行为模式和吸烟对人群宫颈癌患病的影响，在上述模型中添加对特定型别HPV免疫仓室［32］。

2005年，Elbasha等学者为了研究不同亚型HPV感染间的相互关系，使用常微分方程构建了不包含癌前损伤和宫颈癌的人群传递模型，模型结构可概括为对两类亚型HPV易感、感染一种且对另外一种易感、感染两种、感染一种且对另外一种免疫、对一种获得免疫并且对另一种易感、对两种均获得免疫仓室。研究发现，即使不同亚型的感染存在协同作用，多价疫苗对未覆盖的亚型亦可起到保护作用［33］。2007年，Elbasha研究发现，尽管美国已建立筛查机制，对70%的12岁女性接种疫苗仍可以使生殖器疣和宫颈癌的发病率分别下降83%和78%；若同时将12岁男性也纳入国家免疫计划，则这两种疾病的发病率将分别下降97%和91%［34］。因德国的宫颈癌防治策略与其他国家不同，Horn在Elbasha等学者的模型基础上构建了HPV相关疾病的SIR动力学模型［35］。作者认为疫苗的作用将在30年后开始显现，50%的疫苗覆盖率就可降低37%的宫颈癌发病率。

然而，动力学模型也有其弊端，例如，加入了过多的参数，使得动力学模型更加复杂，预测结果可能趋于不稳定［8］；在终生成本和收益核算时，较静态模型复杂。

混合模型

混合模型联合使用上述两类模型，通常将动力学模型的预测结果代入静态模型中，以预测疾病的发展趋势并计算成本和收益。它主要包含两类：联合使用马尔科夫模型和动力学模型，联合使用蒙特卡洛模型和动力学模型。混合模型综合了各类模型的优势，较好地弥补了单一模型的弊端，但模型也更为复杂［36］。

单独使用马尔科夫模型无法测算疫苗的间接收益（人群免疫效应），因此，添加动力学模型以解决此问题。2004年，Taira为了研究仅为女性接种时获得理想收益的条件和是否将男性也加入计划免疫，为Sander的模型［14］添加了动力学模型，构成包含动力学模型和马尔科夫模型的混合模型［37］。该模型中的动力学模型仅包含两个仓室：易感和感染。其研究思路为：根据性别、年龄和性行为对人群分组，首先使用动力学模型预测HPV在人群中的传播过程，然后将所得结果代入马尔科夫模型，预测宫颈癌等疾病的患病率。最为重要的发现是，基于相同的数据，与Sanders的静态模型预测［14］相比，混合模型的预测结果中，单独对12岁女性接种疫苗的成本效益比值下降了约36%，可见人群免疫效应对HPV疫苗经济学评估影响很大。2009年，Anonychuk使用伪动力学法和马尔科夫模型评估了二价HPV疫苗的成本效益［38］。Regan和Kulasingam等学者在定义HPV感染力函数时，使用性伙伴关系变量代替其他研究中的个体行为变量。这一做法有两点好处，一是更容易量化，二是能够抓住性伴侣数这一影响HPV传播的主要危险因素［17，39］。Kulasingam等发现，在考虑人群免疫效应时，联合使用筛查和接种疫苗的干预方案的成本效益比由每生命年51 103美元降低为每生命年36343美元，这一结果再次说明在HPV疫苗经济学评估中，人群免疫效应的重要性［39］。2008年，Usher等学者构建了包含Agentbased动力学模型和基于发病率的静态模型的混合模型［40］。

为了解决个体随机性的原因，哈佛大学的研究者进一步将动力学模型和随机模型联合使用［25，41-43］。Kim和Goldie等研究者从病毒亚型和性别两个角度构建模型：将HPV16和HPV18的疾病自然史分开、对男性和女性分别研究。由此，他们构建了包含未感染、感染、CIN1、CIN2和CIN3、浸润性宫颈癌等25个仓室的动力学模型，以此预测疾病的发病情况，将所得预测数据作为初始条件引入蒙特卡洛模型中，追踪基于个体的整个疾病过程。

总结与展望

本文所综述的2000-2013年文献中，一方面，用于HPV疫苗经济学评估的数学模型的结构越来越复杂，这说明对疾病发展过程的理解逐渐明晰。另一方面，在模型的应用上，采用静态、动力学和混合模型的文献分别为49篇、13篇和8篇，采用静态模型的研究一直占较大比例，但是在近两年文献中，原创性的动力学模型和混合模型仍有出现，然而创新性较大的静态模型鲜见，可见模型的应用整体趋于成熟。总的来说，三类模型各具特色，如动力学模型和静态模型所模拟的人群和参数设定上存在根本性差异［7］，导致各类模型的作用产生较大差异。动力学模型刻画多个不同特征的人群（如按性别、年龄等特征分类）通过性行为相互传染病毒的过程，而静态模型无法刻画这一过程。在参数设定中，动力学模型的病毒感染力与性伴侣数量、人群中已接种疫苗人数等因素相关；而静态模型的HPV感染力不随这些因素变化。因此，这使得静态模型只能计算疫苗的直接收益，相比之下，动力学模型的病毒感染力随着时间变化，模型能够反映出未接种人群的情况，能测算疫苗的直接和间接收益（人群免疫效应），更加全面地测算疫苗的收益。

三类模型所采用的数学理论和实现方法也有较大差异，由此导致各类模型的应用出现很大区别。Canfell认为在疫苗覆盖率较高的假设下，静态模型与动态模型的预测结果较为相近［7］，并且静态模型结构相对简单，较容易实现。在静态模型中，马尔科夫模型是应用最多［7］，但其不能很好地处理事件的随机性和人群的异质性。尽管这一问题在引入蒙特卡洛法之后得到了改善，但是蒙特卡洛模型建模过程较为复杂，使得它的应用受到限制。总的来说，动力学模型估算的收益更加全面，可以与多种其他模型联合使用。因此，未来应关注动力学模型在HPV相关疾病干预方案中的应用，突破现有的一些技术限制，拓展其应用范围。

在目前的研究中，模型准确性仍是一个主要的问题。它主要包括HPV在人群间的传播、疾病发展、疫苗对未覆盖亚型的有效性［44］、自然免疫［45］、防治技术（筛查、诊断和治疗）的有效性和特异性［46］、临床治疗流程、筛查和疫苗接种的覆盖率等方面［7，47］。这主要是因为研究者尚未在疾病、疫苗和诊疗等方面取得统一的共识。尽管如此，通过将模型预测结果与经验数据进行拟合分析，可以在一定程度上提高模型的准确性。此外，随着临床研究的进展和数学模型在HPV相关疾病控制中的应用，研究者可能在上述方面逐渐取得进展，数学模型也将更加贴近现实。

面对HPV相关疾病日益严峻的国内外形势，我国现行的宫颈癌和生殖器疣等HPV相关疾病的防治策略尚不完善，而且我国HPV疫苗经济学评估的研究报告也较少。因此，为了科学地规划疾病干预方案，我们应当积极开展数学模型在HPV疫苗经济学评估中的应用，推动研究成果转化为实践，进而从根本上预防子宫颈癌等疾病，去除子宫颈癌对我国妇女健康的危害；并藉此积极加强数学模型在其他传染性疾病干预政策的研究，使得我国卫生政策的制定更加科学合理，增强我国对传染性疾病的防控能力，尤其是对疾病暴发的应对能力。

1.Forman D，de Martel C，Lacey CJ，etal.Global burden of human papillomavirus and related diseases.Vaccine，2012，30 Suppl5：F12-F23.

2.卫生部.2011年中国卫生统计年鉴，2012.

3.赵娜，赵方辉，高晓虹，等.城市和农村妇女高危型人乳头瘤病毒感染的危险因素分析.中华肿瘤防治杂志，2011，18（16）：1225-1229.

4.王少明，乔友林.HPV预防性疫苗在中国的应用前景.癌症进展，2010，8（2）：134-138.

5.尹畅，李会庆，刁玉涛，等.山东省1970-2005年宫颈癌死亡率变化趋势.中国卫生统计，2009，26（4）：347-349.

6.赵文娟，李永新.大连地区妇女乳腺癌、宫颈癌筛查结果分析.中国卫生统计，2012，29（1）：125-126.

7.Canfell K，Chesson H，Kulasingam SL，et al.Modeling preventative strategies against human papillomavirus-related disease in developed countries.Vaccine，2012，30 Suppl 5：F157-F167.

8.Armstrong EP.Prophylaxis of cervical cancer and related cervical disease：a review of the cost-effectiveness of vaccination against oncogenic HPV types.JManag Care Pharm，2010，16（3）：217-230.

9.王丙刚，曲波，郭海强，等.传染病预测的数学模型研究.中国卫生统计，2007，24（5）：536-540.

10.Stratton KR，Durch JS，Law rence RS.Vaccines for the 21st century：a tool for decisionmaking.National Academ ies Press，1999.

11.Kim SY，Goldie SJ.Cost-effectiveness analyses of vaccination programmes：a focused review ofmodelling approaches.Pharmacoeconomics，2008，26（3）：191-215.

12.彭志行，陈峰.HIV/AIDS传播动力学模型研究进展.中国卫生统计，2011，28（6）：730-734.

13.Dasbach EJ，Elbasha EH，Insinga RP.Mathematicalmodels for predicting the epidemiologic and econom ic impact of vaccination against human papillomavirus infection and disease.Epidemiol Rev，2006，28：88-100.

14.Sanders GD，Taira AV.Cost-effectiveness of a potential vaccine for human papillomavirus.Emerg Infect Dis，2003，9（1）：37-48.

15.Kulasingam SL，Pagliusi S，Myers E.Potential effects of decreased cervical cancer screening participation after HPV vaccination：an example from the U.S.Vaccine，2007，25（48）：8110-8113.

16.Goldie SJ，Grima D，Kohli M，et al.A comprehensive natural history model of HPV infection and cervical cancer to estimate the clinical impactof a prophylactic HPV-16/18 vaccine.Int JCancer，2003，106（6）：896-904.

17.Kulasingam S，Connelly L，Conway E，et al.A cost-effectiveness analysis of adding a human papillomavirus vaccine to the Australian National Cervical Cancer Screening Program.Sex Health，2007，4（3）：165-175.

18.KohliM，Ferko N，Martin A，etal.Estimating the long-term impactof a prophylactic human papillomavirus16/18 vaccine on the burden of cervical cancer in the UK.Br JCancer，2007，96（1）：143-150.

19.Rogoza RM，Westra TA，Ferko N，et al.Cost-effectiveness of prophylactic vaccination against human papillomavirus 16/18 for the prevention of cervical cancer：adaptation of an existing cohortmodel to the situation in the Netherlands.Vaccine，2009，27（35）：4776-4783.

20.Kim JJ.Targeted human papillomavirus vaccination of men who have sex w ith men in the USA：a cost-effectivenessmodelling analysis.Lancet Infect Dis，2010，10（12）：845-852.

21.Bergeron C，Largeron N，M cAllister R，et al.Cost-effectiveness analysis of the introduction of a quadrivalent human papillomavirus vaccine in France.Int JTechnol Assess Health Care，2008，24（1）：10-19.

22.Coupe VM，van Ginkel J，de Melker HE，et al.HPV16/18 vaccination to prevent cervical cancer in The Netherlands：model-based cost-effectiveness.Int JCancer，2009，124（4）：970-978.

23.Thiry N，De Laet C，Hulstaert F，etal.Cost-effectiveness of human papillomavirus vaccination in Belgium：do not forget about cervical cancer screening.Int JTechnol Assess Health Care，2009，25（2）：161-170.

24.Van de Velde N，Brisson M，Boily MC.Modeling human papillomavirus vaccine effectiveness：quantifying the impact of parameter uncertainty.Am JEpidemiol，2007，165（7）：762-775.

25.Kim JJ，Kuntz KM，Stout NK，etal.Multiparameter calibration of a natural history model of cervical cancer.Am JEpidemiol，2007，166（2）：137-150.

26.Chesson HW，Ekwueme DU，Saraiya M，et al.Cost-effectiveness of human papillomavirus vaccination in the United States.Emerg Infect Dis，2008，14（2）：244-251.

27.Chesson HW，Ekwueme DU，Saraiya M，et al.The cost-effectiveness of male HPV vaccination in the United States.Vaccine，2011，29（46）：8443-8450.

28.Vanagas G，Padaiga Z，Kurtinaitis J，et al.Cost-effectiveness of 12-and 15-year-old girls＇human papillomavirus 16/18 population-based vaccination programmes in Lithuania.Scand JPublic Health，2010，38（6）：639-647.

29.Brisson M，Edmunds WJ.Economic evaluation of vaccination programs：the impact of herd-immunity.Med Decis Making，2003，23（1）：76-82.

30.Hughes JP，Garnett GP，Koutsky L.The theoretical population-level impact of a prophylactic human papilloma virus vaccine.Epidem iology，2002，13（6）：631-639.

31.Barnabas RV，Garnett GP.5.The potential public health impact of vaccines against human papillomavirus.HPV Handbood，2004：61.

32.Barnabas RV，Laukkanen P，Koskela P，et al.Epidemiology of HPV 16 and cervical cancer in Finland and the potential impact of vaccination：mathematicalmodelling analyses.PLoSMed，2006，3（5）：e138.

33.Elbasha EH，Galvani AP.Vaccination againstmultiple HPV types.Math Biosci，2005，197（1）：88-117.

34.Elbasha EH，Dasbach EJ，Insinga RP.Model for assessing human papillomavirus vaccination strategies.Emerg Infect Dis，2007，13（1）：28-41.

35.0Horn J，Damm O，Kretzschmar ME，et al.Estimating the long-term effects of HPV vaccination in Germany.Vaccine，2013，31（19）：2372-2380.

36.Marra F，Cloutier K，Oteng B，et al.Effectiveness and cost effectiveness of human papillomavirus vaccine：a systematic review.Pharmacoeconom ics，2009，27（2）：127-147.

37.Taira AV，Neukermans CP，Sanders GD.Evaluating human papillomavirus vaccination programs.Emerg Infect Dis，2004，10（11）：1915-1923.

38.Anonychuk AM，Bauch CT，Merid MF，et al.A cost-utility analysis of cervical cancer vaccination in preadolescent Canadian females.BMC Public Health，2009，9：401.

39.Regan DG，Philp DJ，Hocking JS，et al.Modelling the population-level impact of vaccination on the transmission of human papillomavirus type 16 in Australia.Sex Health，2007，4（3）：147-163.

40.Usher C，Tilson L，Olsen J，et al.Cost-effectiveness of human papillomavirus vaccine in reducing the risk of cervical cancer in Ireland due to HPV types 16 and 18 using a transmission dynam ic model.Vaccine，2008，26（44）：5654-5661.

41.Kim JJ，Andres-Beck B，Goldie SJ.The value of including boys in an HPV vaccination programme：a cost-effectiveness analysis in a low-resource setting.Br JCancer，2007，97（9）：1322-1328.

42.Goldie SJ，Kim JJ，Kobus K，et al.Cost-effectiveness of HPV 16，18 vaccination in Brazil.Vaccine，2007，25（33）：6257-6270.

43.Kim JJ，Goldie SJ.Health and econom ic implications of HPV vaccination in the United States.N Engl JMed，2008，359（8）：821-832.

44.Woertman W，van der W ilt GJ.Estimating the effectiveness of HPV vaccination in the open population：a Bayesian approach.Value Health，2013，16（4）：604-609.

45.Korostil IA，Peters GW，Law MG，et al.Herd immunity effect of the HPV vaccination program in Australia under different assumptions regarding natural immunity against re-infection.Vaccine，2013，31（15）：1931-1936.

46.Chesson HW，Flagg EW，Koutsky L，et al.Modeling the impact of quadrivalent HPV vaccination on the incidence of Pap testabnormalities in the United States.Vaccine，2013，31（29）：3019-3024.

47.Jit M，Levin C，Brisson M，etal.Econom ic analyses to support decisions about HPV vaccination in low-and m iddle-income countries：a consensus report and guide for analysts.BMC Med，2013，11：23.

（责任编辑：丁海龙）

福建省科技厅科技计划项目（2013R0091）教育部人文社会科学研究项目（12YJA790030）；福建省自然科学基金计划资助项目（2012J01303）

1.厦门大学公共卫生学院（361102）

2.卫生技术评估福建省高校重点实验室

3.分子疫苗学和分子诊断学国家重点实验室

4.厦门大学经济学院

5.厦门大学国家传染病诊断试剂与疫苗工程技术研究中心

△通信作者：方亚