平面2-DOF过驱动并联机构控制系统设计

李云龙，何广平

(北方工业大学机电工程学院，北京 100144)

平面2-DOF过驱动并联机构控制系统设计

李云龙，何广平

(北方工业大学机电工程学院，北京 100144)

并联机构运动学控制器忽略了复杂的非线性动力学关系，因此控制器的实际性能往往有限。为此，以提高并联机器人的操作精度为目标，针对2-DOF并联机构，通过建立机构的动力学数学模型及刚度矩阵，设计了计算力矩控制器。基于计算力矩控制器的模型由于考虑了非线性补偿而极大地提高了其控制品质。通过实验将设计的控制器应用到2-DOF并联机构，仿真和实验结果验证了算法的有效性和正确性。

过驱动并联机构;非线性动力学特性;计算力矩控制

过驱动机构是指机构中独立驱动关节数目大于机构自由度数目的一种并联机构。在并联机构中，采用过驱动的优点体现在可以优化输入力、减小机构关节间隙、消除机构奇异点、提高机构的容错性能［1］。例如文献［2］的研究结果表明:过驱动机构能通过合适的非零内力控制来消除机构的结构间隙，提高机构的操作精度。过驱动机构只存在于并联机构中［3］，采用过驱动技术，并联机构的力奇异问题能得到缓解或消除［3］，从而提高了系统的力操作性能。过驱动并联机构在工业领域中应用广泛，例如并联机床中［4］、仿生机械［5］和高性能战机等。

目前，大多数机器人的控制器都采用运动学控制器。这类控制器忽略了各关节间的耦合关系和动力学特性，而并联机构的非线性动力学特性尤为突出，因而在并联机构的应用中往往无法达到预期控制品质。为此，非线性控制系统被提了出来，在非线性控制系统中，计算力矩控制是最简单、有效的。它与PD控制相比，增加了内环控制，完成了线性补偿，使得并联机构系统跟踪误差小，抗干扰能力强。近些年，这一算法在机器人领域逐渐成为研究热点。H CHENG等的研究结果表明:在高速下计算力矩控制的精度比PD控制要高得多［6］。L S GUO等将自适应的计算力矩控制用于2-DOF并联机械手的轨迹跟踪［7］。据此，以平面2-DOF四分支过驱动并联机构为研究对象，根据拉格朗日方法建立其动力学模型。仿真和实验结果表明，所设计的算法实现了满意的控制品质。

1 系统结构

如图1所示，平面2-DOF并联机构拥有4条运动链，4条运动链结构相同，各个运动链的一端用铰链连接于一点，该点为末端执行器，另一端与驱动电机相连，这端为驱动关节。机构末端执行器自由度数为2，而驱动关节数目为4，故该机构为过驱动并联机构［10］。

由于该机构具有中心对称结构，并联机构的Lagrange函数就等于4个运动链的Lagrange之和，故对一个运动链进行动力学分析即可。图2所示为并联机构简图，坐标系XOY的原点位于正方形A1A2A3A4中心。机构的8个连杆长度均为0.2 m，基座X、Y方向的间距均为0.4 m。

图1 平面四分支过驱动并联机构实物

图2 平面四分支过驱动并联机构简图

2 动力学方程建模

针对过驱动并联机构的特点，采用拉格朗日方法建立其动力学方程，拉格朗日方法是以系统动能和势能建立动力学方程，其推导过程比较简单，而且清楚地表示出各构件的耦合特性。

设机构的第i条分支链的2个连杆相对于重心的转动惯量分别为Iai、Ibi，杆质量分别为mai、mbi，rai是连杆AiBi重心到点Ai的距离，rbi是连杆BiC到点Bi的距离。由于平面机构势能为零，在建模过程中只考虑系统的动能，则该支链的拉格朗日函数为:

由于4个分支链的结构相同，所以并联机构的Lagrange函数为:

记并联机构关节向量为q=［qa1qa2qa3qa4qb1qb2qb3qb4］T，关节力矩向量为τ= ［τa1τa2τa3τa4τb1τb2τb3τb4］。并将Lagrange函数式 (2)代入如下的Euler-Lagrange方程:

可以得到并联机构的动力学模型为:

由并联机构的运动学关系，可以得到如下的闭链约束方程:

求式 (5)关于时间的微商，可以得到并联机构的速度约束条件:

其中:A(q)是并联机构的速度约束矩阵。

在式 (4)的动力学模型上，加入约束内力ATλ，可得:

式中:λ是一个未知乘子，代表了约束力的大小。

选择并联机构末端执行器坐标qe=(x，y)作为并联机构动力学模型的独立变量，记q关于qe的速度雅克比矩阵为S，可知:

将式(8)代入式(6)，可以得到如下关系式:

由于式 (9)的为任意末端执行器速度向量，故可推出AS为0矩阵，其转置矩阵为:

用雅可比矩阵的转置ST左乘式(7)，将式(8)和式(10)代入式(7)，可以将并联机构的动力学模型简化为如下形式:

记主动关节力矩为τa，记主动关节矢量关于末端qe的速度雅克比矩阵为J，可知STτ=JTτa，从而得到工作空间的动力学模型为:其中，J的定义为:

其中:Me=STMS表示工作空间的惯性矩阵;Ce=STM˙S+CS表示工作空间的科里奥利力与向心力矩阵。式 (12)所表示的动力学模型中仅含有两个方程，而驱动力矩τa有4个独立变量，因此驱动力矩τa的解不唯一。为了使得并联机构的控制输入最小、运动控制更平滑，可采用欧式范数最小的驱动力矩作为解:

式中:(JT)+=J(JTJ)－1为矩阵JT的伪逆。

3 运动控制系统设计及实验

3.1 控制系统及稳定性分析

控制系统主要由上位控制计算机、四轴运动控制卡 (固高科技)、直流伺服驱动器和自带光电编码器的直流伺服电机四部分组成。计算机内的PCI插槽嵌有四轴运动控制卡，计算机通过运动控制卡获取机构的当前状态和完成相关控制，同时记录实验数据。图3为控制系统简图。

图3 运动控制系统组成

控制系统中的控制器采用计算力矩控制算法［8，11］，用计算力矩设计控制方案的基本思路是:先引入控制:

这样受控机构方程为:

消去非线性项后化为:

因M是可逆阵，故上式转化为一个解耦的线性定常系统:

式中Kp和Kv均为正定矩阵，这样闭环系统方程为

从而由Kp和Kv的正定性知 (e，˙e)=(0，0)是全局渐进稳定的平衡点，这就实现了全局稳定的轨迹跟踪。

针对平面2-DOF四分支过驱动并联机构控制算法计算如下:

3.2 计算力矩控制器仿真验证

在MATLAB软件的Simulink［9］模块中，建立过驱动并联机构的物理模型和控制模型，运用控制模型驱动机构运动，得到末端的仿真轨迹，并将其与理论期望轨迹相比较，从而验证控制模型的正确性。

给机构末端规划圆轨迹运动:以 (0.06，0)为圆心，0.06 m为半径的圆。圆轨迹的运动速度为0.2 m/s。图4—6分别表示在计算力矩控制时圆轨迹的主动关节力矩输出、主动关节角位移误差和在操作空间末执行器的轨迹误差。

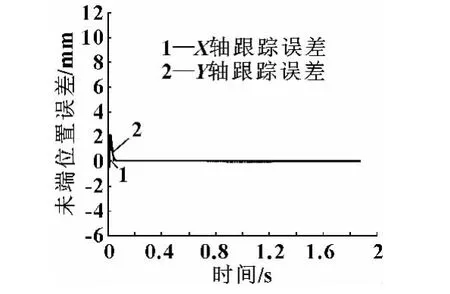
图6 圆轨迹的跟踪误差

从所得到的仿真曲线图中可以看出，并联机构在作圆周运动和正弦曲线运动时，末端运动比较平稳，跟踪误差收敛于0。这说明，计算力矩控制可以消除机构末端的轨迹跟踪误差及外部干扰的影响。

3.3 控制实验及结果分析

搭建实验平台用于平面四分支过驱动并联机构的轨迹跟踪控制实验。实验平台如图1所示，并联机构由4个直流伺服电机驱动，电机带有光电编码器进行角度测量，用固高科技公司的运动控制卡 (GT-400-SV-PCI)完成伺服电机控制。实验中的运动控制程序用Visual C++编写，控制算法中包含数字滤波运部分，可执行程序如图7所示。

图7 应用程序

选取工作空间中的圆周轨迹作为并联机构末端执行器期望运动轨迹规划操作末端运行一个以 (0.06，0)为圆心、0.06 m为半径的圆。图8、图9分别表示末端执行器位置跟踪曲线和轨迹跟踪误差。误差产生的原因主要包括建模误差、忽略了摩擦力、机构间隙等。

图9 圆轨迹的跟踪误差

图8 圆轨迹的末端执行器位置输出

4 结论

针对平面2-DOF四分支过驱动并联机构进行了动力学建模，将设计的控制算法应用于平面2-DOF四分支过驱动并联机构，实现了圆轨迹实时控制。实验结果表明:该控制系统相对于传统PD控制［10］具有更好的轨迹跟踪性能，实验结果达到满意精度。为了进一步提高控制精度，可以在末端执行器增加力传感器和位置传感器，形成全闭环控制系统。

［1］吴宇列，吴学忠，李圣怡.2-DOF冗余平面并联机构的奇异位形与冗余性研究［J］.机械设计与研究，2002，18 (2):23－25.

［2］MULLER A.Internal Preload Control of Redundantly Actuated Parallel Manipulators:Its Application to Backlash A-voiding Control［J］.IEEE Transactions on Robotics，2005，21(4):668－677.

［3］DASGUPTA B H，MRUTHYUNJAYA T S.Force Redundancy in Parallel Manipulators:Theoretical and Practical Issues［J］.Mechanism and Machine Theory，1998，33 (6):727－742.

［4］KIM J，FRANK C P，SUN J R，et al.Design and Analysis of a Redundantly Actuated Parallel Mechanism for Rap id Machining［J］.IEEE Transactions on Robotics and Automation，2001，17(4):423－434.

［5］LEE J H，YI B J，OH S R，et a l.Optimal Design and Development of a Five-bar Finger with Redundant Actuation［J］.Mechatronics，2001，11(1):27－42.

［6］CHENG H，YIU Y K，LI Z X.Dynamics and Control of Redundantly Actuated Parallel Manipulators［J］.IEEE/ASME Transactions on Mechatronics，2003，8(4):483－491.

［7］GUO L S，ZHANG Q.Adaptive Trajectory Control of a Two DOF Closed-chain Robot［C］//Proceedings of the American Control Conference，Arlington，2001:658－663.

［8］吴军，李铁民，关立文.飞行模拟器运动平台的计算力矩控制［J］.清华大学学报:自然科学版，2006，46(8): 1405－1408.

［9］张志勇.ATLAB教程－基于6.x版本［M］.北京:北京航空航天大学出版社，2001.

［10］高煊，何广平.一种过驱动并联机构的运动学分析及控制系统设计［J］.机床与液压，2009，37(12):163－167.

［11］丛爽，尚伟伟.并联机器人［M］.北京:电子工业出版社，2010.

Control System Design for the Planar 2-DOF Overactuated Parallel Mechanism

LI Yunlong，HE Guangping
(College of Mechanical and Electrical Engineering，North China University of Technology，Beijing 100144，China)

In parallel mechanism kinematics controller，the complex nonlinear dynamics relationships are ignored，so the actual performance of the controller is often limited.For this，to improve the operation accuracy of parallel robot，aiming at the 2-DOF parallel mechanism，through establishing the dynamic mathematical model of mechanism and stiffness matrix，a computing torque controller was designed.Because in the model based on computing torque controller，nonlinear compensation was considered，so the control quality was enhanced greatly.The designed controller was applied to the 2-DOF parallel mechanism，simulation and experimental results verified the correctness and effectiveness of the algorithm.

Overactuated parallel mechanism;Nonlinear dynamics characteristic;Computing torque control

TH113

A

1001－3881(2014)9－029－4

10.3969/j.issn.1001－3881.2014.09.008

2013－03－27

北京市优秀人才培养基金资助项目 (20051D0500201)

李云龙 (1984—)，男，研究生，主要研究方向为并联机构、运动控制等。E－mail:jd06063221@126.com。