SETAR模型在中国股市波动率研究中的应用

莫达隆

（贺州学院，广西 贺州 542899）

SETAR模型在中国股市波动率研究中的应用

莫达隆

（贺州学院，广西 贺州 542899）

文章对上证指数2006年1月6日-2011年5月23日收盘价的波动率进行了研究，介绍并使用随机系数SETAR模型与ARCH族模型进行对比拟合，根据数据的特点，文章构建了一种新型的SETAR模型，即AR(r)-SETAR(l，p1，p1)模型，模型利用ADF检验和AIC准则进行识别和估计。结果表明：可用AR(4)-SETAR(2，1，1)模型来拟合中国股市中的上证指数，研究其波动率特点，上证指数波动率呈不对称的响应，而且“负”响应比“正”响应高出约1.3倍。用ARCH族模型也证明了这种不对称响应的特征，但无法度量波动的强度，预测效果也没有SETAR模型精确。说明上证指数波动率不对称响应明显且呈现非线性的趋势，这种非线性的趋势更适合用SETAR模型来拟合。

SETAR模型；股市风险；金融经济；金融投资

一、波动率模型研究综述

波动率作为度量股市市场风险的重要指标之一，一直以来都是学术界和金融界的研究对象。在现代金融经济理论中，波动率是期权定价理论最具关键的定价因素，波动率在金融经济学的其他领域也得到广泛的应用。波动率模型不仅可以帮助投资者进行资产投资的最优化组合，还可以帮助投资者分析和度量投资的风险水平。

自Engle于1982年提出ARCH模型以来，关于金融风险和波动率研究的波动率模型成为学术界和金融界研究的重点。ARCH模型在提示金融市场价格的波动规律方面取得了辉煌的成就，自问世以来，该模型己被广泛应用于经济与金融领域的时间序列数据的分析，成为资产定价和投资组合风险评估的重要工具，ARCH模型可以更容易解释所建立的模型和作出更准确的波动预测。但ARCH模型假定正的响应和负的响应对波动率的影响是相同的，因为在ARCH模型中波动率依赖于以往响应的平方，实际上，大量数据表明，金融市场价格对正的响应和负的响应的反应是不同的。

此后，许多经济学家对ARCH模型进行了扩展。其中贡献最突出的是波勒斯列夫(BollerSlve，1986)提出的广义自回归条件异方差模型(AGRCH)，这一模型认为，误差项的方差不仅取决于误差项过去的方差，而且还取决于过去的误差项本身。由Li1ine(1987)提出了ARC+M模型，把条件方差放到条件平均数方程中。Nelsno(1991)提出了EARCH，进一步考虑了信息不对称现象的正负冲击所引起的不同影响。Bailleie et 1a(1996)年提出了FIAGRCH模型，该模型能较好的反应序列变动异方差的特性和长记忆变动特性，描述了过去的冲击持续到未来，并对未来的预测产生很大的影响。在利用ARCH族模型预测波动率的同时，国外学者的研究结果也大大的丰富了其他波动率的模型。如随机波动模型(VS)、马尔科夫机制转换模型(MRS)以及阀值模型(T)等。其中ARCH模型和VS模型是最常使用的两个模型。所以近年来又出现了这些模型互相结合的趋势，如马尔科夫机制转换模型和自回归条件异方差模型(SARHC)相结合的模型。

目前国内对股票波动率的研究主要集中在实证应用研究上。在2000年张思奇的文章中运用ARMAARC+M模型对1992年l月2日到1998年6月3日的上证综指成分股进行实证研究，结果表明，我国股市的有效程度已经得到明显提高，市场己具备某些弱势有效市场特征。刘秀芳的“中国股市趋向弱势有效之实证研究”运用有效市场理论分析了相关研究中存在的问题，最后得出中国股票市场正趋于弱势有效的结论。徐龙炳、陆蓉(1999)对中国股票市场进行了RS/分析，结果得到沪、深股市Hurst指数分别为0.661和0.643，表明中国股市存在状态持续性，股指所构成的时间序列呈非线性；徐响龙(2001)运用稳态分布实证研究中国股市收益分布的特征等。陆静利用回归分析的方法研究了天气对股票市场波动率的影响，发现除极端天气（如灾害性的天气）外，其他天气对股票市场的波动率是没有影响的。张普等人基于无套利原理和期权定价理论，建立起波动性价值模型，他们认为波动率对股票市场的影响没有波动性价值那么大，即现金红利率是影响股票市场的首要因素。与此同时，跟随国外研究的步伐，越来越多的研究成果（包括模型、检验方法等）将被使用到我国股市中进行波动率研究，对我国股市的认识的进一步提高也指日可待。陈浪南等人构建一种混合GARCH跳跃模型来探讨股票市场资产收益的跳跃行为与股票市场波动率的关系，结果发现条件波动率与跳跃行为之间存在相互的直接回馈效应。周春生推广了Mei、Wu& Zhou(2005)的模型（简称MWZ模型），在市场不允许卖空的条件下，得到交易型价格操纵发生的条件，他们认为在股价被操纵的过程中，换手率与回报波动率之间存在较强的正相关关系[1]。

SETAR模型被成功地用来预测一些生物和物理方面的进程，如预测lysn数据和太阳黑子的数目(Tong，1990)，此外该模型在经济和金融方面也得到了广泛的应用。Tiaoand Tsay(1994)，Potter(1995)运用该模型对美国的GDP进行了预测；Potter(1995)、Peel and Speight(1995)年分别运用SETAR模型对美国和英国的GDP进行了预测，但是运用该模型对股票进行研究的文章一直较少。Ruey S.Tsay成功地利用SETAR模型对1962年7月3日-1999年12月31日的IBM股票的日收益率进行建模，证实IBM股票的日对数收益率只有很弱的序列相关性，然而均值方程的新息过程表现出强烈的相依性和正、负收益率的不对称响应。胡进在他的博士学位论文中，对SETAR模型的参数估计提出一种全新的方法，即方差比统计量估计，并利用全局搜索算法解决SETAR模型的参数估计的问题，最后他用这种模型研究了中国经济增长中的非线性特征和不对称响应特征[2]。但这种不对称响应强度如何度量？目前文献还没有进行讨论，本文在研究中国股票波动率特征的同时拟给出波动率不对称响应的强度度量方法。

二、随机系数SETAR模型

1.随机系数SETAR模型定义如下

其中，Y是观测值xt，t=p+1，p+2，…，n。

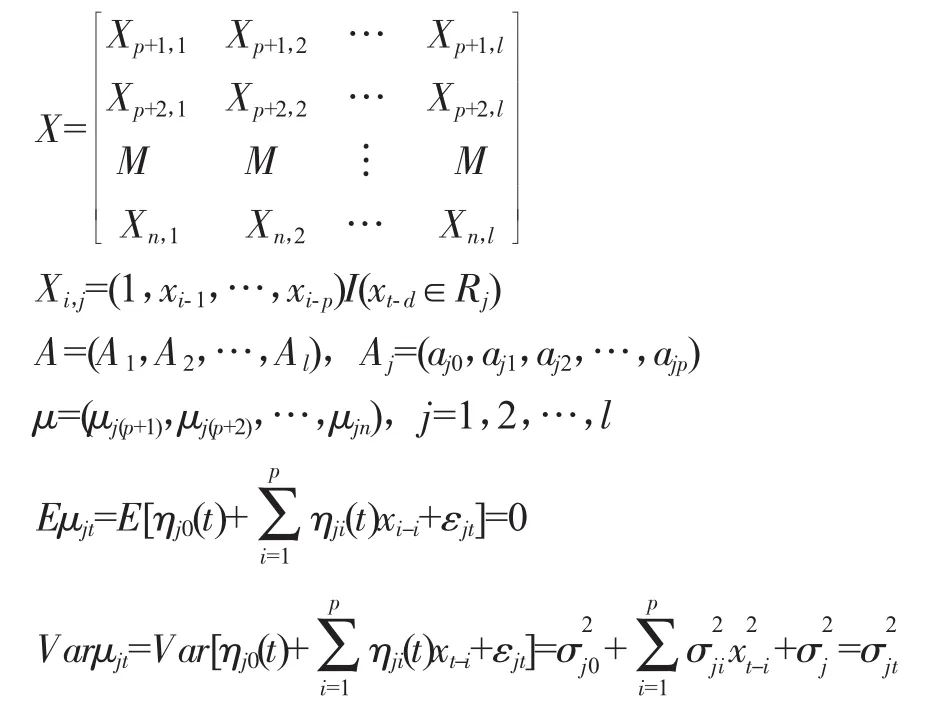
式(1)为随机系数n维p阶SETAR模型，记为SETAR(l，p，p)。

要估计的参数是l，A，σ2jt，d，p，通常参数l可根据数据实际情况来定，参数d与分割Rj有关，A是一个条件最小二乘估计值。对于参数d和分割Rj（通常可用序列的滞后项来表示），可以先固定某一个值，然后比较其残差平方和，选取其最优者。

2.随机系数SETAR模型的参数估计

式(1)的参数估计为：

其中，D=diag(dp+1，dp+2，…，dn)是权矩阵，

3.随机系数SETAR模型的检验

随机系数SETAR模型的检验有三个方面：

（1）残差检验

残差检验主要是残差的独立性、正态性和等方差性等检验。

（2）非线性检验

随机系数SETAR模型是一个非线性模型，我们采用的非线性检验是广义似然比检验方法，这个方法对SETAR模型有很好的功效[3]。

H0∶a1i=a2i=…=ali，i=0，1，2，…，p

H0∶a1i，a2i，…，ali，i=0，1，2，…，p不全相等

构造其统计量为：

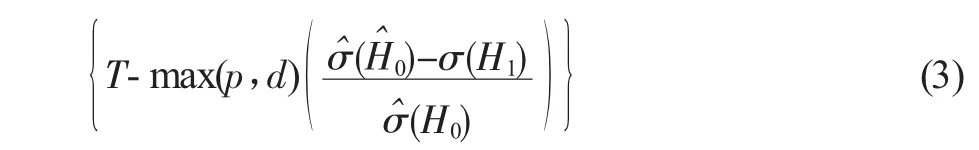
其中σˆ(H1)和σˆ(H0)分别是在备择假设H1和原假设H0成立时的极大似然估计。当H0成立时(3)式取值为较小的数。

（3）显著性检验

显著性检验用于检验模型系数的是否显著，预测效果是否良好。

三、实证研究

本文选取上证指数2006年1月6日-2011年5月23日收盘价（设为序列{pt}，t=1，2，…，1307），共1307个数据。定义对数收益率rt=ln(pt)-ln(pt-1)，利用计量经济学软件包Eviews进行统计分析。

1.收益率rt的统计性质

图1是收益率序列{rt}在Eviews描述性统计分析的结果：收益率在样本期内的均值为0.000654，标准差为0.020005，偏度为-0.438228，小于正态分布的偏度值0，峰度为5.427814，高于正态分布的峰度值3，正态性检验JB统计量为362.5486，说明收益率rt具有尖峰和厚尾的特性，与正态分布显著不同。利用Eviews对序列{rt}进行ADF检验：在0.01的显著水平下，拒绝存在一个单位根的原假设，表明{rt}是平稳的（表1）。上述结论与国内外对波动率研究的结果是一致的。

图2描述了上证指数收益率的时间序列。该序列图表明上证指数的收益率在一些时期的波动比较大，且负向波动大于正向波动。再对比日期来看，每年的1月份至3月份和5月份至8月份的负向波动比其他时期要大很多，说明上证指数在春节先后和夏季的波动率较大。

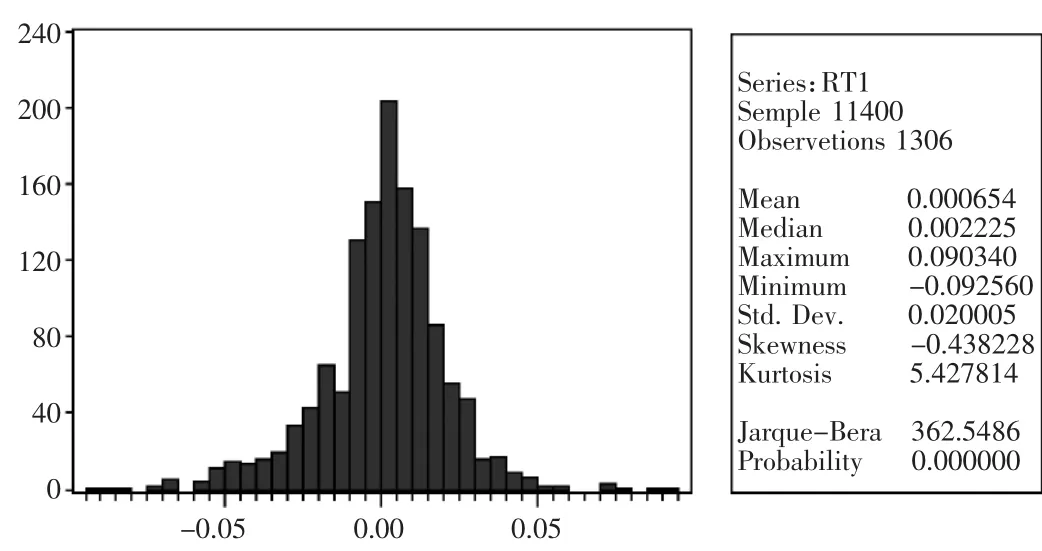
图1 收益率rt的描述性统计量

表1序列{rt}ADF检验结果

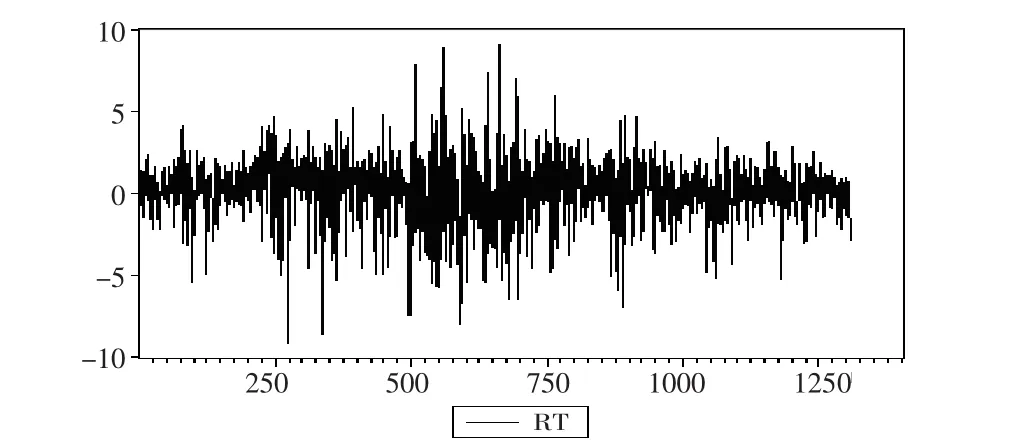
图2 上证指数收益率的时间序列图

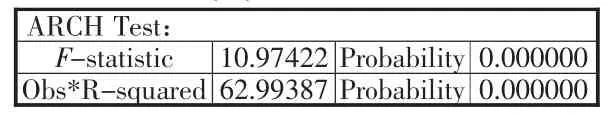
表2序列{εt}的ARCH-LM检验

2.ARCH效应检验

把收益率序列{rt}写成：

rt=b+εt

其中b为常数项，εt为误差项。对序列{εt}进行ARCH效应检验结果如表2，相伴概率p值远远小于显著水平0.05，因此拒绝原假设，可以认为序列{εt}存在ARCH效应，有必要进行ARCH族模型建模分析。

3.ARCH族模型建模分析

利用Eviews软件，可以建立ARCH及其多种扩展模型。

结果如表3所示，ARCH-M模型的残差平方和最小，而且AIC值和SC值也比较小，可以认为ARCHM模型拟合优度最佳。GARCH-M模型是GARCH模型的改进模型，它是在GARCH模型的基础上增加了条件方差项。SQRT(GARCH)后的系数是条件方差的系数（如图3），有时也称为风险溢价参数，其代表是资产回报期望风险的大小，此时风险溢价参数值是-0.047138＜0，即该时段的上证指数的收益率与它过去的波动率成反比（与此不同的是，西方成熟的股市市场的风险溢价参数往往表现为正值，即收益率与过去的波动率成正比[1]），说明上证股市还存在高投机性和高换手率。风险溢价参数的P值=0.6092，远远大于0.05，拒绝为0的原假设，说明期望风险显著，投资风险大，股市存在短线投机观念还相当浓厚的非理性投资行为。与GARCH(1，1)模型相比，GARCH-M模型的残差平方和、AIC和SC值都要小许多，说明GARCH-M模型对GARCH模型具有改进的作用。

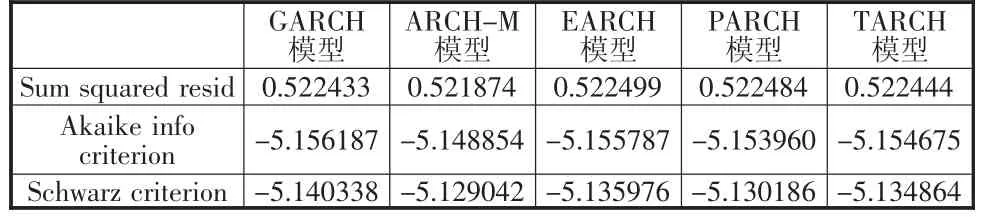
表3 序列的ARCH族Eviews软件拟合结果对比表

图3 GARCH-M模型参数估计与检验结果

对于股票市场的研究发现，股票下跌和上涨相同幅度时，股票价格下跌过程往往会伴随着更剧烈的波动性。为描述这种现象，可以引入ARCH模型的其他扩展模型。其中EARCH模型、TARCH模型和PARCH模型可以用于描述波动率的这种非对称性质，用Eviews估计EARCH模型（结果如图4），结果中的RESID(-1)^2*(RESID(-1)＜0)（即C(4)） 项代表杠杆效应系数的估计值，其不等于0，说明信息的作用是非对称的，小于0时认为杠杆效应显著，而且从另一个侧面说明上证指数的收益率与它过去的波动率成反比。通过观察，在其他非对称ARCH模型，如TARCH模型和PARCH模型中都呈现了显著的杠杆效应，说明上证指数的收益率序列{rt}存在显著的杠杆效应。

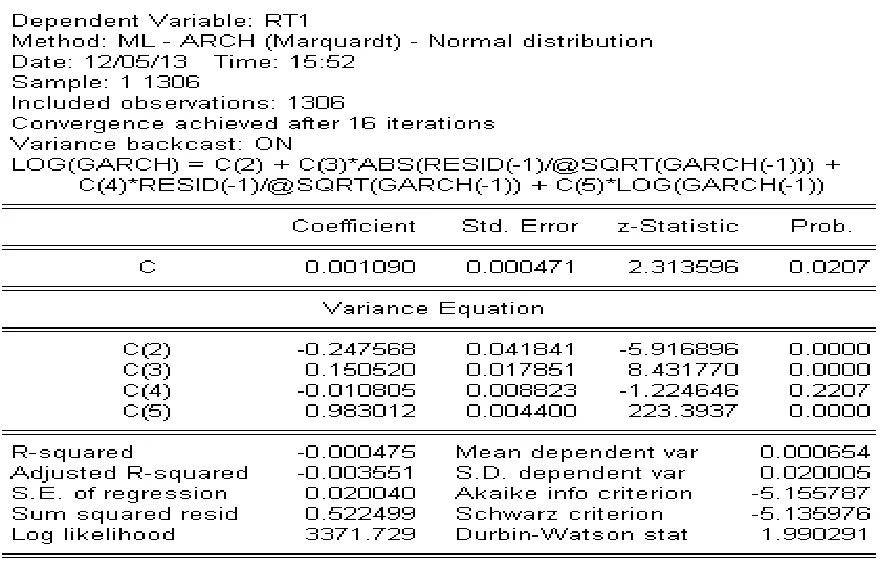
图4 EARCH模型参数估计与检验结果

杠杆效应是指股市价格变动与其随机波动率负相关，波动率对价格的上升和下降的反应是不同的，也就是说收益率为负时的波动性比收益率为正时的波动性要大一些。换言之,“好”和“坏”的消息会对未来的价格波动产生不同程度的影响，通常“坏”消息所引起的波动更大。EARCH模型就是为了描述波动率的这种不对称特性而提出来的，但在这里EARCH模型的预测效果却没有ARCH-M模型的预测效果那么好，而且EARCH模型也没能定量地给出波动率不对称响应的强度大小。为了进一步刻画序列{rt}的这种不对称的响应，下文试以随机系数SETAR模型来对比尝试。

4.随机系数SETAR模型建模分析

（1）模型的识别与估计

在前面对收益率序列{rt}进行ADF检验时，发现收益率序列{rt}的滞后4期存在显著相关，可以考虑先建立AR(4)模型，经尝试有：

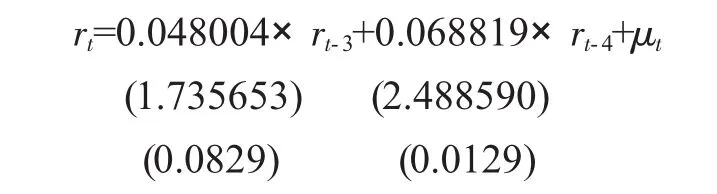
其中μt是残差项，第一行括号是T值，第二行括号是P值，系数显著，说明的确存在4期滞后项。

然后对序列{μt}建立SETAR模型。波动率研究的是正、负收益率的不对称响应，因此实际应用中可初步设置l=2，门限值r=0。门限变量和滞后项数p则由AIC准则进行选择，最后选取rt-1为门限变量和滞后项数p=1，即可建立二维一阶随机系数SETAR模型：

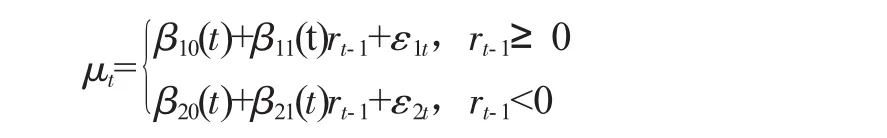
其中r为门限值，βji(t)=βji+ηji(t)，t=1，2，…，n

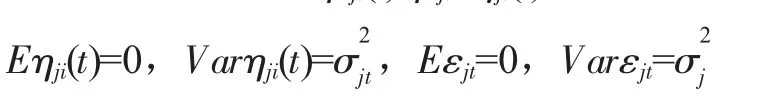
经利用Eviews进行编程计算，模型估计结果为：

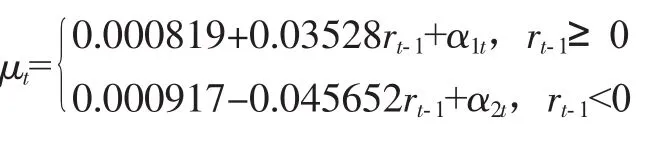
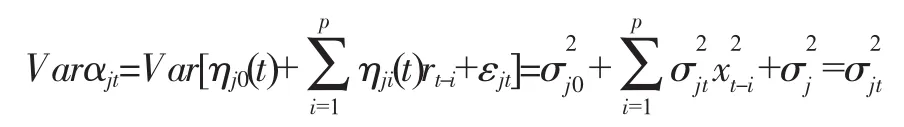
上述模型可记为AR(4)-SETAR(2，1，1)模型，从模型可以看出，当收益率为负时引起的波动强度比收益率为正时引起的波动强度要强一些，而且“负”响应比“正”响应高出约1.3倍。

（2）对AR(4)-SETAR(2，1，1)模型进行检验

先对模型进行残差检验，经检验模型的残差平方和为0.521337，残差自相关检验结果如表4。

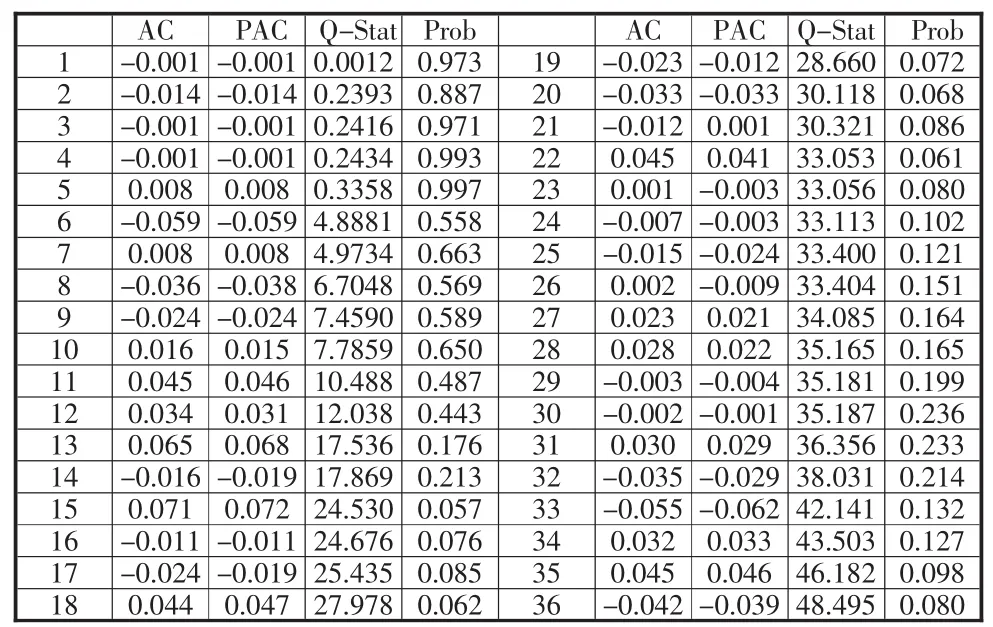
表4 对序列{rt}建立AR(4)-SETAR(2，1，1)模型的残差自相关检验结果

表4给出了从滞后1到36阶自相关检验的Q统计值和假设自相关系数为0的p值，结果表明：在显著水平为0.05下，不能拒绝原假设，即所有的自相关系数为0，因而残差是不具有自相关性，或者说对序列{rt}建立AR(4)-SETAR(2，1，1)模型是合适的。

再对模型进行非线性检验，采用广义似然比检验，有如下结果：

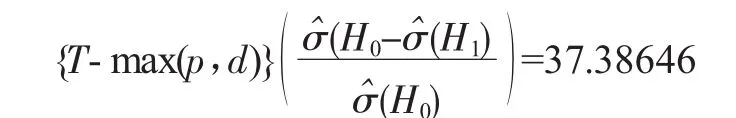
该值远远大于水平0.1%的临界值27.20，拒绝H0假设，即线性模型的假设不成立[7]。

最后是模型系数的显著性检验，计算结果表明：两分段的系数中截矩项系数不显著而滞后1期项的系数都比较显著。

上述结果说明所建立的AR(4)-SETAR(2，1，1)模型对数据拟合效果是理想的，结论可信，预测准确。

四、结论

第一，上证指数的收益率是随机平稳的时间序列，ARCH模型和ARCH-M模型表明：上证指数收益率的风险溢价参数值是-0.047138＜0，即上证指数的收益率与它过去的波动率成反比（与此不同的是，西方成熟的股市市场的风险溢价参数往往表现为正值），说明上证股市还存在高投机性和高换手率。风险溢价参数的P值=0.6092，远远大于0.05，拒绝为0的原假设，说明期望风险显著，投资风险大，股市存在短线投机观念还相当浓厚的非理性投资行为。

第二，上证指数的收益率在一些时期的波动比较大，模型还表明上证指数的收益率在春节先后和夏季期间的波动率比其他时期要大，而且都呈负向波动。即上证指数的收益率存在春节假期的负向效益和夏季的负向效益，这对投资者有较好的警示作用。

第三，ARCH扩展族模型EARCH模型、TARCH模型和PARCH模型建模结果表明，上证指数的收益率的信息作用是非对称的，存在较显著的杠杆效应，且负向波动大于正向波动。说明中国股市市场在受到不利消息和收到有利消息时有明显的不同反应，意味着中国股市市场正朝着一个有效的市场迈进，中国股市市场在逐步走向完善。

第四，通过上述的对比，用SETAR模型来拟合中国股市中的上证综合指数，其效果明显优于ARCH族模型，可用AR(4)-SETAR(2，1，1)模型来拟合中国股市中的上证指数，研究其波动率特点，结果表明上证指数波动率呈不对称的响应，而且“负”响应比“正”响应高出约1.3倍。说明中国股市在不同的状态下具有不同的性质，中国股市呈现非线性的趋势，这种非线性的性质更适合用SETAR模型来拟合。

[1]易丹辉.数据分析与Eviews应用 [M].北京：中国人民大学出版社，2008.

[2]陆静.中国股票市场天气效应的实证研究 [J].中国软科学，2011(6)：65-78.

[3]张普，吴冲锋.股票价格波动：风险还是价值？[J].管理世界，2010(11)：52-60.

[4]陈浪南，孙坚强.股票市场资产收益的跳跃行为研究 [J].经济研究，2010(4)：54-66.

[5]周春生.中国股票市场交易型的价格操纵研究 [J].经济研究，2005(10)：70-78.

[6]胡进.SETAR模型与冲击效应的理论与应用研究 [D].武汉：华中科技大学，2010.

[7]范剑青，姚琦伟，陈敏译.非线性时间序列-建模、预报及应用[M].北京：高等教育出版社，2005：101-103.

[8]Ruey S.Tsay，潘家柱译.金融时间序列分析 [M].北京：机械工业出版社，2009：118-123.

（责任编辑：FMX）

SETAR Model in the Chinese Stock Market Volatility

MO Da-long
（Hezhou University，Hezhou Guangxi 542899，China）

The volatility of closing price in the Shanghai Securities Composite Index from January 6，2006 to May 23，2011 is studied.Random coefficient SETAR model and ARCH model are used to do comparison and fitting.According to the characteristics of data，a new SETAR model is constructed，i.e.AR(r)-SETAR(1，p1，p1)model，which is identified and estimated by ADF test and AIC criterion.The results show that the Shanghai Composite Securities Index of the Chinese stock market can been fitted by the AR(4)-SETAR(2，1，1)model.It is shown that the volatility of Shanghai Securities Composite Index admits asymmetrical response，and negative response ratio was about 1.3 times higher than positive one.The ARCH family model also proves the asymmetric response，but it can not measure the intensity fluctuations，and prediction is less accurate than the SETAR model.The volatility of Shanghai index admits asymmetry response and exhibits nonlinear trend.This nonlinear trend is more suitable for SETAR model.

SETAR model；The stock market risk；The financial economy；The financial investment

F830.91

A

1004-292X（2014）03-0073-05

2013-08-19

2011年度广西高等学校科研一般资助项目（200103YB141）；2012年贺州学院科研资助项目（2012PYZK02）。

莫达隆（1970-），男，广西蒙山人，副教授，主要从事概率统计研究。