联合GNSS和GRACE数据分析南极跟踪站的径向形变

李伟伟 鞠晓蕾 沈云中 张子占

（1同济大学测绘与地理信息学院，上海200092；2同济大学空间信息科学与及可持续发展应用中心，上海200092；3中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，湖北武汉430077）

0 引言

利用GNSS跟踪站长期观测数据确定的地壳运动信息（如速度场）对地球动力学的研究发挥了重要的作用。影响GNSS跟踪站速度场估计精度的主要因素包括跟踪站坐标序列的长度，周期信号的合理建模，有色噪声正确确定。通常要求坐标序列的时间跨度大于2.5年，考虑周年与半年周期项［1］，顾及闪烁噪声和随机游走噪声两类有色噪声才能准确估计GNSS跟踪站的速度及其精度［2-6］。近年来，卫星重力测量（如GRACE）从质量变化的角度分析径向形变也得到了应用。Davis等［7］首次分析比较了亚马逊流域GRACE时变重力资料与GNSS坐标序列，两者具有较好的一致性。Van Dam等［8］比较分析了欧洲区域GNSS与GRACE 34个月估计得到的地表垂直位移，并将两者呈现较低相关性的原因归结于GNSS数据处理模型的不准确，且在沿海区域的站点表现更明显。随后，Tregoning等［9］在 Van Dam研究基础上，重新处理GNSS与GRACE数据，两者的相关性有了明显提高，接近25%的站点相关系数都大于 0.5。Tesmer等［10］分析全球区域 115个站GNSS站观测坐标和GRACE估算得到的径向位移序列，60%站相关系数达到0.5以上，34%站相关系数在0和0.5之间，还有6%站呈现负相关。可见，不同区域GNSS与GRACE相关程度不同。

基准站速度主要包括大尺度板块运动，局部构造形变和冰后回弹三种地壳形变因素的综合影响。基准站位于基岩上且在板块内部相对稳定，就可消除局部构造形变的影响。而板块运动一般沿水平方向，此时的径向变化则主要是冰后回弹引起的地壳形变［11］。Bevis等［12］利用西南极 GNSS观测网坐标序列获得径向形变值，并比较了 ICE-5G（VM2），IJ05（6A），RF3S20（β＝0.2）以及 HUY09m四种GIA模型的预测径向形变值。观测径向形变值与预测径向形变值之差的经验分布函数表示四种GIA模型均存在低估形变或高估形变的现象。埃尔斯沃斯山脉和东南极沿海区域的GNSS站径向形变结果与前两种GIA模型预测值比较同样有一定的偏差［12］，并按站点分析了其偏差的可能原因。

本文主要利用GNSS数据分析南极区域的噪声特性和形变速度，并与GRACE时变重力场结果进行比较分析，研究两者在径向位移的相关性，且比较了GNSS估计形变与GIA模型（W12a）预测站点形变。

1 数学模型

1.1 GNSS估计形变

GNSS跟踪站坐标序列通常可以用线性趋势项、周年和半年项、阶跃变化项和噪声项表示［14］，即

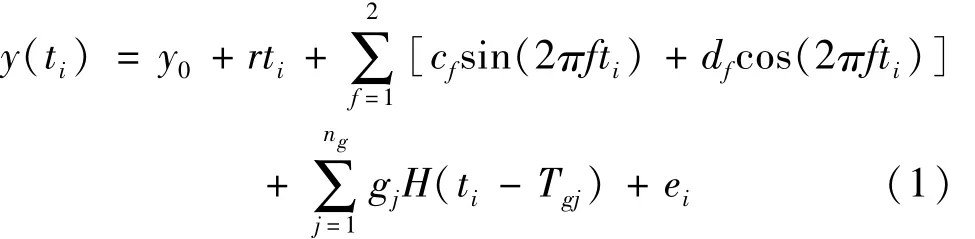
式中ti是以年为单位的GNSS站点单日历元，y0为常数项，r为线性速度，cf和df表示周期性运动（f＝1表示年周期项，f＝2表示半年周期项），表示发生在历元Tgj大小为gj的阶跃，H表示阶梯函数。按照最小二乘参数估计的函数模型，式（1）可以改写为

其中y为观测值向量，A为设计矩阵，x＝［y0，r，c1，d1，c2，d2，g1，…，gng］为待估的模型参数，e为观测噪声向量。若Σy为观测值的协方差矩阵，则基于最小二乘准则求得的参数估值及其协方差阵为

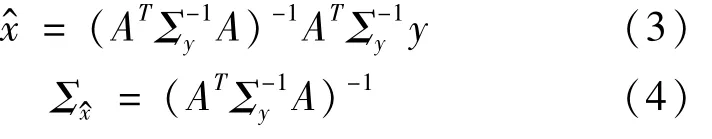
考虑到白噪声、闪烁噪声和随机游走噪声的影响，观测值的协方差矩阵Σy可表示为

其中U1，U2，U3分别为上述三种噪声的协因数阵，θ1，θ2，θ3为对应的噪声分量［3］，采用方差-协方差估计公式可计算各种噪声分量的估值［15］。

1.2 GRACE估计形变

由GRACE估计的径向位移可用（6）式表示，

其中，Δr为地球表面径向位移变化，R为地球的平均半径（6 378.136 km），θ、λ分别为余纬和经度，Nmax为最大阶数为完全规格化的勒让德函数，ΔClm和ΔSlm为每月Stokes系数与系数平均值之差，h′l及 k′l为 l阶负荷勒夫数，Wl为高斯滤波函数，主要用来减小高阶系数本身误差导致的影响。本文采用Han等［16］提供的负荷勒夫数，取Nmax为60，高斯滤波半径为 500 km［17］。

2 数据处理与结果分析

2.1 数据介绍

2.1.1 GNSS数据

由于南极区域各跟踪站建站时间不同，因此各站采集的数据时间段也不同。为了与GRACE数据时间统一，本文选取了南极大陆12个时间跨度为2004—2012年的GNSS站点作为分析对象，每站数据长度不少于3年。各站经纬度和时间跨度如表1所示。图1为选取的GNSS站点分布，除CRAR站和MCM4站处于火山地带外，其他站均建立在基岩上。

表1 南极GNSS站数据概况Table 1.Data overview of GNSS stations in Antarctica

图1 南极GNSS站点分布Fig.1.Distribution of GNSS stations in Antarctica

2.1.2 GRACE数据

本文采用的GRACE数据为2012年3月CSR（Centre for Space Research）公布的GSM RL05数据，其时间跨度为2004年1月到2012年6月，共99个月的数据。该数据采用了新的地球物理模型（海洋、大气、潮汐等），其空间分辨率、精度和周期性变化特性等都优于RL04数据［18］。由于GRACE GSM模型已经扣除海洋大气等的影响，因此在与GNSS数据进行对比时，需要加回level 2数据中反映海洋和大气质量变化引起的时变重力场信息的GAC产品系数；此外，为了使GRACE数据能够与GNSS数据的参考框架统一［19］，需要考虑GRACE数据的一阶项［20］。

2.2 结果分析

2.2.1 噪声分量

表2列出了各站估计的白噪声、闪烁噪声和随机游走噪声分量，由此可明显看出南极GNSS跟踪站的观测噪声中白噪声并不是主要的噪声，因此对其形变速度进行估计时只顾及白噪声的影响是不符合实际的。另外，除MCM4站以外，大部分站点均不存在随机游走噪声或其分量较小，这可能是由于MCM4站附近的火山运动引起基岩不稳定造成的［21］。

表2 噪声分量Table 2.Noise component

2.2.2 相关性比较

如2.1节所述，GNSS与GRACE数据的时间分辨率不同，为了比较GNSS和GRACE去除线性趋势项的形变数据，本文对GNSS数据进行了月平均。图2为12个站点的径向月变化比较图（蓝色为GNSS，红色为GRACE），可见GNSS和GRACE确定的形变总体趋势一致，但前者的变化振幅比后者大。为了研究GNSS和GRACE的相关性，计算了两者相关系数（如表3，显著性水平为0.05）。结果显示两者的相关系数最大可达0.663，总体上呈现较强的相关性。

2.2.3 径向形变速度比较

表4列出12个站点GNSS估计的径向形变速度和W12a模型预测的形变速度。GNSS结果显示位于南极半岛的OHI3和PALM站的径向形变速度最大，12个站中4个站下降，但变化趋势均比较缓慢。由于CRAR站和MCM4站位于火山活动地区，其形变速度不能准确反映形变趋势。其他10个站形变方向基本一致，且6个站与W12a模型吻合较好，W12a模型在DEVI站和DUM1站较高估计形变，而在南极半岛较低估计形变。

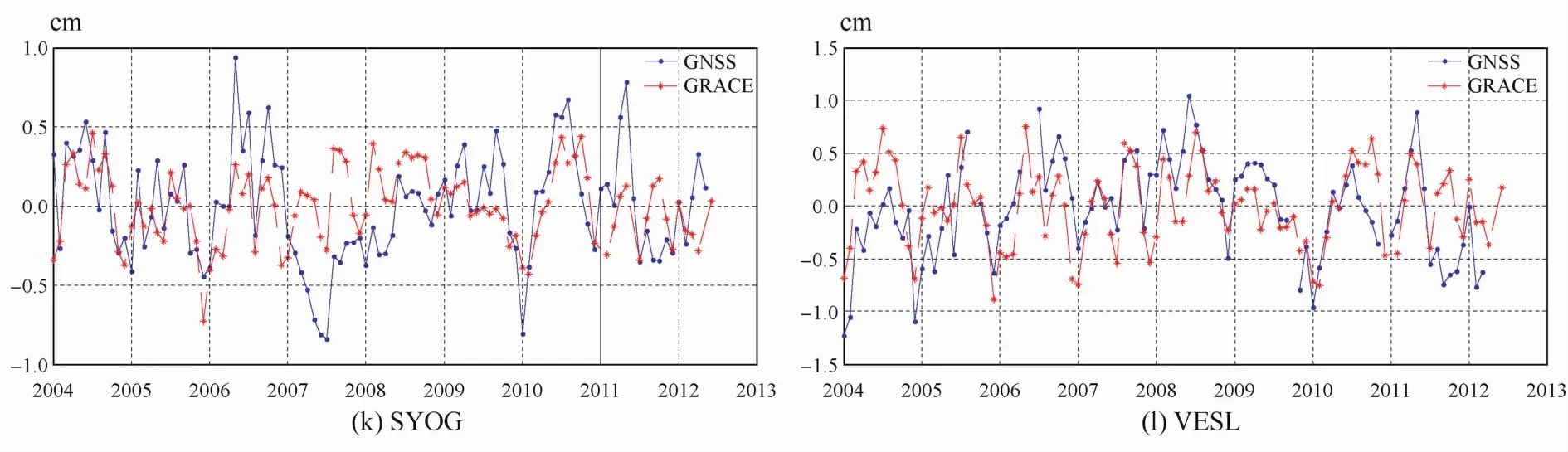
图2 GNSS与GRACE数据求得的径向坐标月变化Fig.2.Vertical displacements derived from GNSS and GRACE data

表3 GNSS与GRACE数据求得的径向坐标相关系数Table 3.Correlation coefficient of GNSS and GRACE

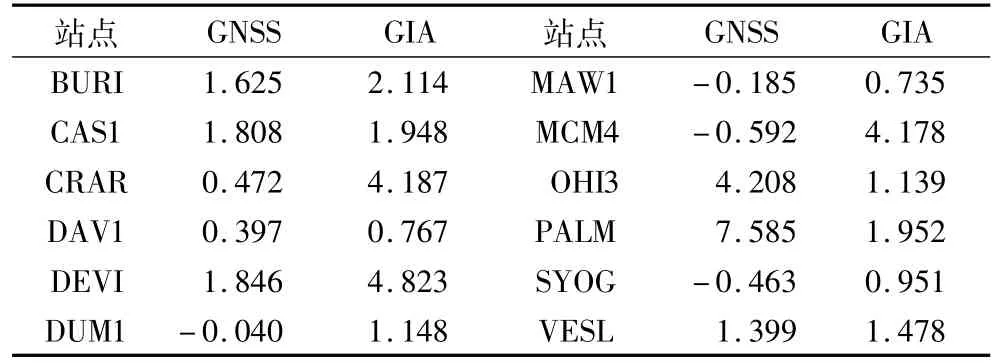
表4 站点速度（mm·a－1）Table 4.Velocities of GNSS stations（mm·a－1）

3 结论

本文计算了GNSS与GRACE月平均坐标的相关性，顾及有色噪声估计南极GNSS站点的径向形变，并比较分析了GNSS站估计形变和GIA模型预测形变。主要得出以下结论：

（1）南极GNSS坐标序列的观测噪声主要是白噪声和闪烁噪声，然而部分站（如MCM4站）受当地环境影响随机游走噪声更明显，因此在估计形变速度时，只考虑白噪声是不准确的。

（2）南极区域GNSS站序列与GRACE序列的相关系数最大为0.663，总体呈现较强的相关性。

（3）虽然研究站点形变趋势总体与W12a模型相吻合，但是需要更多的站点来分析两者的吻合度。

1 Blewitt G，Lavallée D.Effect of annual signals on geodetic velocity.Journal of Geophysical Research，2002，107（B7）：2145，doi：10.1029／2001JB000570.

2 Zhang J，Bock Y，Johnson H，et al.Southern California Permanent GPSGeodetic Array：Error analysis of daily position estimates and site velocities.Journal of Geophysical Research，1997，102（B8）：18035—18055.

3 Mao A L，Harrision C G A，Dixon T H.Noise in GPS coordinate time series.Journal of Geophysical Research，1999，104（B2）：2797—2816.

4 Teferle F N.Strategies for Long-term Monitoring of Tide Gauges Using GPS.Nottingham：University of Nottingham，2003.

5 Santamaría-Gómez A，Bouin M N，Collilieux X，et al.Correlated errors in GPS position time series：Implications for velocity estimates.Journal of Geophysical Research，2011，116（B1），doi：10.1029／2010JB007701.

6 LiW W，Shen Y Z.Velocity estimation of GPS base stations considering the coloured noises.Journal of Applied Geodesy，2012，6（3-4）：149—157.

7 Davis JL，Elósegui P，Mitrovica JX，et al.Climate-driven deformation of the solid Earth from GRACE and GPS.Geophysical Research Letters，2004，31（24），doi：10.1029／2004GL021435.

8 Van Dam T，Wahr J，Lavallée D.A comparison of annual vertical crustal displacements from GPS and Gravity Recovery and Climate Experiment（GRACE）over Europe.Journal of Geophysical Research，2007，112（B3），doi：10.1029／2006JB004335.

9 Tregoning P，Watson C，Ramillien G，et al.Detecting hydrologic deformation using GRACE and GPS.Geophysical Research Letters，2009，36（L15401），doi：10.1029／2009GL038718.

10 Tesmer V，Steigenberger P，Van Dam T，etal.Vertical deformations from homogeneously processed GRACE and global GPS long-term series.Journal of Geodesy，2011，85（5）：291—310.

11 朱新慧，孙付平.用甚长基线干涉测量数据检测冰期后地壳回弹.地球物理学报，2005，48（2）：308—313.

12 Bevis M，Kendrick E，Smalley R，etal.Geodeticmeasurements of vertical crustal velocity in West Antarctica and the implications for icemass balance.Geochemistry Geophysics Geosystems，2009，10（10），doi：10.1029／2009GC002642.

13 Argus D F，BlewittG，PeltierW R，etal.Rise of the Ellsworthmountainsand partsof the EastAntarctic coastobserved with GPS.Geophysical Research Letters，2011，38（16），doi：10.1029／2011GL048025.

14 Rosanne N.Observation of Geodetic and Seismic Deformation with the Global Positioning System.San Diego：University of California，2002.

15 Li B F，Shen Y Z，Lou L Z.Efficient estimation of variance and covariance components：A case study for GPS stochasticmodel evaluation.IEEE Transactions on Geoscience and Remote Sensing，2011，49（1）：203—210.

16 Han D Z，Wahr J.The viscoelastic relaxation ofa realistically stratified Earth，and a further analysisof post-glacial rebound.Geophysical Journal International，1995，120（2）：287—311.

17 Jekeli C.Alternative methods to smooth the Earth’s gravity field.Department of Geodetic Science and Surveying.Ohio：Ohio State University，1981.

18 Bettadpur S.Product Specification Document.Center for Space Research，The University of Texas at Austin，2007-b.

19 Swenson S，Chambers D，Wahr J.Estimating geocenter variations from a combination of GRACE and ocean model output.Journal of Geophysical Research，2008，113（B8），doi：10.1029／2007 JB0 05338.

20 Crétaux JF，Soudarin L，Davidson F JM，et al.Seasonal and interannual geocentermotion from SLR and DORISmeasurements：comparison with surface loading data.Journal of Geophysical Research，2002，107（B12）：2374，doi：10.1029／2002JB001820.

21 Raymond C A，Ivins E R，Heflin M B，et al.Quasi-continuous global positioning system measurements of glacial isostatic deformation in the Northern Transantarctic Mountains.Global and Planetary Change，2004，42（1-4）：295—303.