燃烧器头部旋流器旋流槽加工误差分析及工艺改进

曹卫亮，张喆

燃烧器头部旋流器旋流槽加工误差分析及工艺改进

Processing Error Analysis and Process Improvement of Hydrocyclone Circumrotate Channel at Burner Head

曹卫亮，张喆

在燃烧器的结构中，头部旋流器旋流槽的大小对出风量、风速以及火焰长度有直接的影响，但是在实际的旋流槽加工中，由于多方面的影响，旋流槽宽度误差较大，本文就实际的旋流槽加工工艺进行了实验分析，并对工艺计算方式进行了优化，大幅提高了旋流槽加工精度。

1加工误差的问题描述

典型头部旋流槽加工图如图1所示。

在前期加工过程中，旋流槽的误差形式表现为：梯形截面的上口符合尺寸、下口超差，超差值在0.8～1mm左右，误差数值较大，具体检验数据见表1。

这样的误差直接影响了燃烧器整体质量，也导致了多件产品的报废，对公司造成了一定的损失。

2加工误差的理论分析

经过对旋流槽的整个加工工艺、设备、人员操作等方面进行分析，产生误差的原因主要有以下几个方面：

2.1 机床精度问题

（1）主轴垂直度误差。垂直度误差会导致槽形变化，但由于旋流槽的槽深尺寸很小（一般为10～ 15mm），因此在这个加工方向上产生的误差值，不会成为超差的主要原因。

（2）传动稳定。铣床传动链的稳定性主要体现为刀具摆动，而通过分析该铣床加工其他工件，特别是加工矩形截面旋流器的情况，我们认为刀具摆动产生的误差应在精度允许的范围内。

（3）挂轮误差。挂轮误差主要反映在螺旋角度上，不会产生在槽宽方向上。但挂轮传动不平稳，使导轨与分度头之间的合成运动产生一定的振动，直接体现在被加工工件表面的法线方向（误差敏感方向）上，对加工精度的影响较大。

图1 典型头部旋流槽结构图

表1 典型头部旋流器旋流槽误差，mm

（4）分度头误差。分度头可以对工件进行准确的圆周分度，但旋转任意角度时，手柄转过孔盘会用某一近似值代替，存在分度误差。不过分度误差较小（角度误差一般在15″之内），反映到弦长上的误差可以不计。

2.2 刀具及切削参数

（1）刀具为定尺寸高速钢立铣刀，其直径不会产生误差。铣刀出现崩刀时，能够做到及时更换或刃磨，而且刃磨质量较好。

（2）立铣刀本身的摆动会造成尺寸的超差，当切削参数选择不合理时，摆动会加大。但通过工艺检查发现，操作者选取的切削参数比较合理。高速钢立铣刀切削米数一般控制在18m/min以下，每齿进给量0.03mm，吃刀量5～6mm。

2.3 操作累积误差

全程跟踪、观察操作者的操作过程，发现在刀具对中、偏移工件、吃刀深度、分度计算、摇动孔盘、挂轮确定螺旋角、旋转工件、刀具找线、刀具入程出程等具体加工环节上，存在一定操作误差。

但通过量化分析，发现上述每项误差值均不大，且操作误差属于随机误差，不会产生如此有规律且方向一致的误差。

2.4 拟合原理误差

在机械零件加工中，某些曲面只有通过现代智能加工手段才能完全准确加工，因此在普通机床上，我们往往会采取近似的加工运动或刀具轮廓，这样就导致了拟合原理误差的产生。但经过分析认为，螺旋槽的拟合原理误差主要反映在槽的底面而不是侧面。

2.5 工艺原理问题

在普通铣床上使用普通刀具加工螺旋槽，其加工原理是利用挂轮控制螺旋角，利用刀具与工件的偏移控制梯形夹角，利用分度头旋转工件控制槽宽。其具体加工过程是：

刀具对中→首次偏移工件→加工首槽的第一个侧面→依次旋转工件、依次加工其他螺旋槽的第一个侧面→反向偏移工件→旋转工件→加工首槽的第二个侧面→依次旋转工件、依次加工其他螺旋槽的第二个侧面。

对以上工艺顺序反复检查，工艺原理没有问题。

2.6 计算方法问题

使用电脑模拟方法，全程验证原计算方法。通过对φ175（12mm/ 9mm）、φ212（15mm/9mm）两种规格旋流器进行模拟加工，发现加工后的法向截面槽宽尺寸为“12mm/ 9.48mm”、“15mm/11.83mm”，这是在不考虑其他因素情况下、直接产生的误差，误差值与工件实际超差值很接近。

2.7 误差分析（表2）

通过定量分析，发现计算方法及反向偏移这两个因素是导致槽宽超差的主要原因：

（1）加工第一个侧面时，原加工方法按法向尺寸偏移，与工件的安装反运行轨迹不符，应该按其在端面的投影尺寸偏移（按法向尺寸偏移，会造成梯形角度变小）。

（2）加工第二个侧面时，反向旋转角度的计算过程非常复杂，而且在旋转过程中累计误差也较大。

3计算方法改进与工艺优化

针对以上分析的结果，考虑采用新的计算方法和刀具找线方式，减小旋流槽加工误差。

3.1 优化计算方法

（1）将槽宽的法向尺寸换算成端面投影尺寸（以15mm/11mm为例，见图2）

（2）按投影尺寸计算偏移量（见图3）

（3）导程计算

式中：

L——导程

D——工件外径

β——螺旋升角

（4）挂轮计算

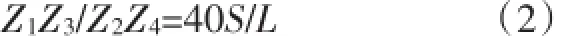
式中：

L——导程

S——工作台丝杠螺距

40——分度头定数

Z1、Z3——主动轮齿数

表2 对造成误差产生的各因素分析

图2 投影尺寸计算

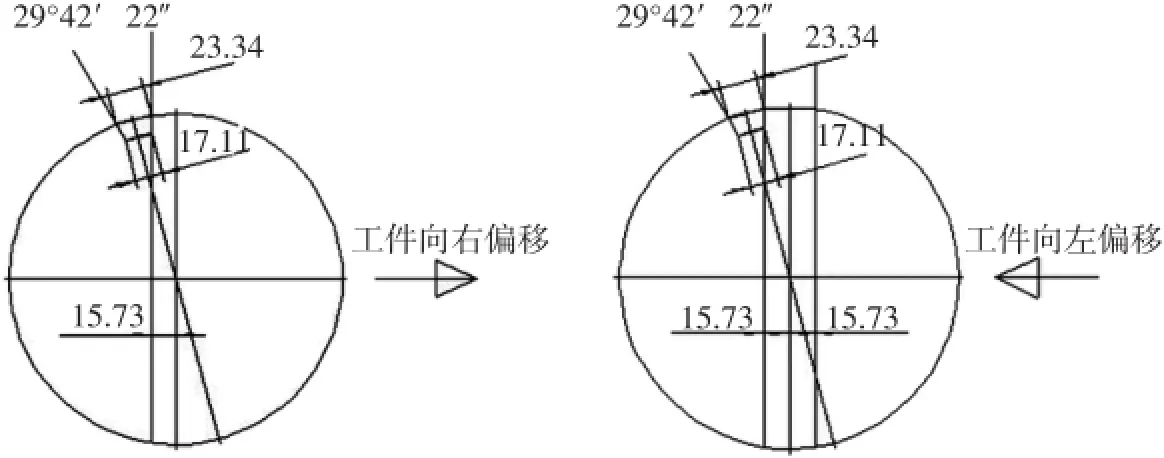
图3 偏移量计算

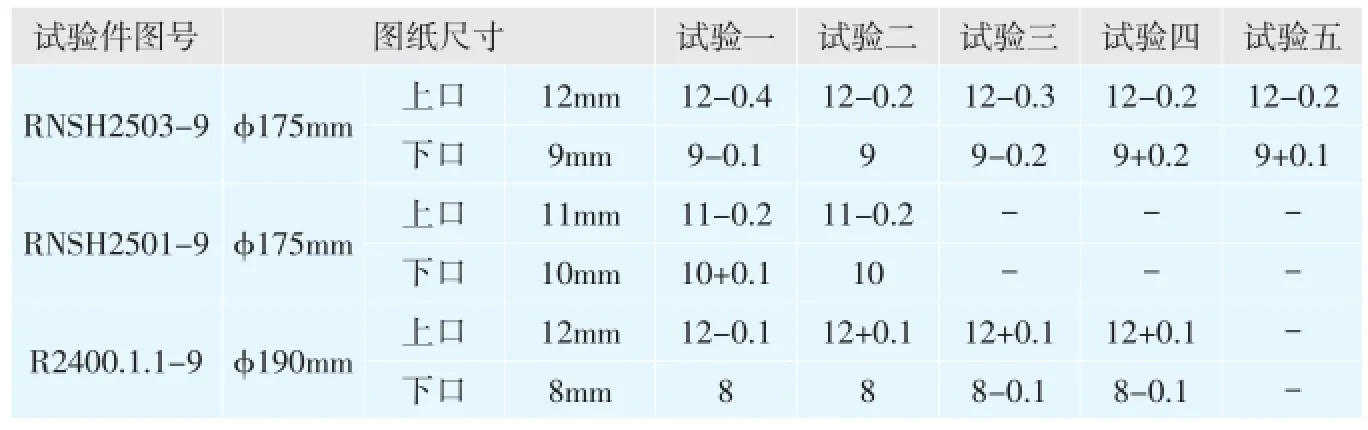
表3 新计算方法试验数据

Z2、Z4——被动轮齿数

（5）分度计算

式中：

n——手柄转数

θ——所需转动角度，°

3.2 优化工艺

加工第二个侧面时，不再按照计算角度旋转，而是按照“按上口尺寸划线、用刀具找线、保证上口尺寸”的方法旋转。这种方法本身，不仅理论上相当于按照计算角度旋转，而且跳过许多中间环节，有效进行了误差转移（见图4）。

3.3 新工艺方法实践

按照新的计算方式，进行若干次试验，误差结果见表3。从表3可以看出，产生的误差由以前的0.8～1.0mm下降至0.1～0.4mm（主要分布在0.1～0.3mm），误差明显减少。误差方向由以前的仅下口超差，变为上口和下口均有少量超差情况，误差方向较随机，较之前的方式有了较大的改善（见表3）。

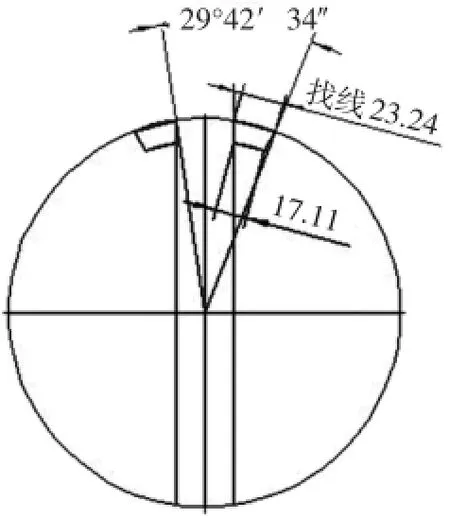
图4 优化后的方案

4结论

（1）在加工工艺、设备刀具、操作人员不变的情况下，计算方法与反向旋转是影响旋流槽宽度误差的主要原因。

（2）计算中按照法向尺寸偏移产生的误差较小，类似件均可采用该计算方式以减小加工误差。

（3）该计算方式较原方法有了较大改善，有效保证了头部旋流槽在燃烧器中所起作用。

[1]成胜.变导程螺旋线圆柱凸轮的加工误差研究[J].机械工程师,2008（4）.

[2]王虎勤.基于SolidWorks的刀具螺旋槽的模拟加工分析[J].金属加工,2010（18）.

[3]许茏,胡剑.加工螺旋槽的成形铣刀轮廓数学计算编程及建模仿真[J].工具技术,2010（7）.

[4]天津大学.机械原理[M].人民教育出版社,北京：1979.■

TQ172.625.3

B

1001-6171（2014）02-0052-03

中材（天津）重型机械有限公司，天津300400；

2013-07-13；编辑：孙娟