基于BP神经网络的车辆动态称重技术

熊少康，王凌川，章家岩，郭许林，冯旭刚

(1.安徽工业大学电气与信息工程学院，安徽马鞍山243032；2.马鞍山钢铁股份有限公司物资公司，安徽马鞍山243000)

动态称重是智能交通系统的重要组成部分，快速、准确地测量汽车载质量对于公路交通的有效运营、管理、养护、执法等具有重要的意义。在动态称重出现之前，车辆称重采用静态方式，即车辆静止于称重传感器上进行质量测量，这种称重方式可达到很高的精度，但是要求车辆在过秤时必须停车，称量时间长，工作效率低。由此可见，对于控制车辆超载运输或物流仓储等要求连续称重的场合(如采矿、冶金、煤炭等货物运输行业以及公路运输行业)，迫切希望实现动态称重[1-3]。对于动态称重，汽车通过称台时，其作用在称台上的力除了自身重量外，还受很多因素干扰，如车速、车辆振动、路面平整情况等[4-5]。若干扰信号混入汽车的真实轴重信号，会给信号分析带来很大的困难。虽然现有的动态称重算法如算术平均法、位移积分法等[7]可在一定程度上解决高频及随机信号干扰问题，但是这些方法都是对单个的数据波形进行处理，从中提取相关的特征值，从而得出轴重。另外它们大多依赖于车型，不具备普遍适用性。在实际使用时，由于受到称重时间较短、传感器灵敏度差、采样速度有限、采集数据不足等因素的影响，导致动态称重精度下降，难以满足要求[7-8]，研究新的动态称重算法对于提高动态称重精度极其重要。文中采用神经网络技术[9-10]对动态称重系统进行建模，利用BP神经网络的非线性函数逼近能力，预测称重系统的位移最大超调量和车辆静态重量。

1 动态称重过程动力学分析

车辆动态称重系统(如电子汽车衡、轨道衡)一般为典型的二阶欠阻尼系统[11-13]，其力学模型如图1。图中：M为被测车辆的质量；m，f和k分别为称重装置的质量、系统的机械阻尼和弹簧的劲度系数；x(t)为M和m共同的位移信号，即系统的模拟输出。

图1 动态称重系统数学模型Fig.1 Dynamic weighing system model

假定M和m从时间t=0时一起振动，则可得系统的动力学方程

其中：u(t)=Mgε(t)；系统阻尼比；系统无阻尼自振角频率由(2)式可得动态称重过程中的位移响应曲线，如图2。由图2可知该系统满足二阶欠阻尼条件，阶跃响应是衰减的正弦振荡曲线。位移响应的峰值时间为

将式(3)代入式(2)，整理后可得二阶欠阻尼系统的最大超调量为

式(4)显示了车辆动态称重系统中，系统阶跃响应的最大超调量x(tp)与车辆的质量M呈单调递增的函数关系，M越大，超调量x(tp)越大。峰值时间反映了时域动态快速性，最大超调量则反映系统响应平稳性的性能指标。因此，选取神经网络的输入、输出变量分别为振荡系统的最大超调量和车辆的静态重量，利用神经网络模型建立输入与输出之间的非线性函数关系，并通过系统的学习和训练后，完成动态称重过程的车辆静态重量计算。

图2 控制系统的动态性能指标Fig.2 Dynamic property target of control system

2 动态称重BP神经网络算法设计

利用神经网络模型建立输入与输出之间的非线性函数关系，并通过系统的学习和训练后，即可完成动态称重过程的车辆静态重量计算。BP网络具有良好的自我学习能力，其神经元采用的传递函数通常是Sigmoid型可微函数，可以实现输入和输出间的任意非线性映射。尤其是在训练样本足够全的情况下，能很高精度地逼近期望的非线性映射。

2.1 输入和输出变量的选取

选取振荡系统的最大超调量作为神经网络的1个输入，利用神经元网络良好的逼近能力[15]，增强器鲁棒性，将输出回馈到输入端作为1个输入信号。因此，选取最大超调量、输出反馈2个量为BP网络的输入。网络输出即为静态轴重，输出变量为车辆的静态重量。网络层数决定了称重模型的辨识精度，增加输入与层数可以降低误差，提高精度，但也使网络复杂化，从而增加了网络权值的训练时间。因此，称重模型采用的是1个S型隐含层和1个线性输出层的神经网络，通过增减隐含层神经元的个数来调节其辨识精度。

2.2 训练算法设计

采用CC(Cascade-Correlation)算法[9]，该算法是增长法中的1种，经编程计算，确定出动态称重模型隐层神经元个数为5。由于系统是非线性的，初始权值的选取对于权值学习过程的误差性能函数能否达到全局最小、是否收敛以及训练时间的长短有很大影响，取初始权值为(-1,1)之间的随机数。

在整个训练过程中整体误差表示为

从输出层开始，考虑到权值的影响，输出层的输入表示为

对于第i隐层，考虑权值的影响，输入之和表示为

其中α，β为学习率。

将式(8)代入Sigmoid函数得到该层的输出

输出误差可以通过BP网络从输出层回传到输入端，对输出层误差可表示为该层输入值偏导的形式

同理，对于隐层单元

BP神经网络训练算法采用动量法和学习率自适应调整的策略[10]，以利于提高网络的学习速度并增强算法的可靠性。动量法权值调整算法为

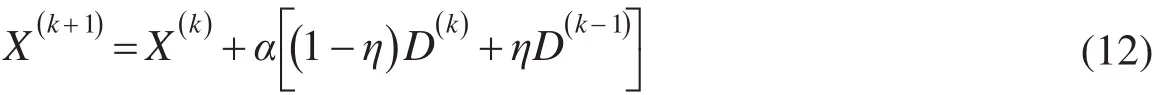
其中：X(k)是第k步时，由网络的权值和阈值组成的向量；D(k)为负梯度；α为学习率，α>0；η为动量因子，0≤η<1。加入的动量项相当于阻尼项，可减少学习过程的振荡趋势，从而改善收敛性。

自适应调整学习率的权值调整算法为：

当连续2次迭代其梯度方向相同时，表示下降太慢，这时可使学习率加倍；当连续2次迭代其梯度方向相反时，表示下降过头，这时可使学习率减半。

将以上2种方法结合，可得到动量—自适应学习率BP神经网络的权值修正算法

3称重过程仿真分析

设计小车以最大超调量为神经网络1个输入进行动态称重实验[14]。当小车静态负载分别为5,6,7,8,9,10 kg时，其输出电压的最大值(即振荡系统的最大输出值y(tp)分别为1.2，2.74，4.19，5.73，7.27，8.80 V。用测量数据对神经网络离线学习，得到最终的模型结构，即隐层和输出层的权值和阈值矩阵，分别为：

隐层权值矩阵 [-4.224 8 0.459 2-1.277 9 1.543 7 2.311 3]T

隐层阈值矩阵 [15.944 5 13.028 9 9.296 5-5.860 7-1.817 4]T

输出层权值矩阵 [1.211 1 1.380 1-1.034 1 2.280 5 3.248 1]

输出层阈值矩阵 [3.309 2]

在仿真过程中，取m=1 000 kg，实际车辆质量M为1 000～50 000 kg之间的6个值，采样周期T=0.5 ms，K=50 000 N/mm，f=200 N/(mm/s)。在MATLAB 7.0.1环境下，用M文件编写程序进行仿真，结果如表1。

表1 动态称重过程仿真结果Tab.1 Simulation results of dynamic weighing system

根据表1可以看出：网络输出值与真实质量非常接近，仿真误差低于千分之一，说明该方法具有极高的精度；从所列峰值时间tp可见，质量M越大，峰值时间tp越长。故在动态称重时，质量较大的车辆需以较低速度运行，以保证有较长的称量时间。实际上，大吨位车辆难以达到很高的速度，而小质量汽车反而可以高速行驶，文中所述方法与实际相符，具有很强的实用性。

如果车辆过衡速度进一步提高，则车辆过衡时间将缩短，计算机所采集数据将会进一步减少。如果车辆过衡时间小于峰值时间，将出现不能采集到最大超调量的情况，利用最大超调量求解静态车重的方法将无法应用，为了解决这个问题，可以采用下均方误差比较法和神经网络预测方法。在现场采集足够多的样本，建立样本库。实际测量过程中，将采集到的未知车辆数据与样本库中各样本进行比较，选取其中均方误差最小样本的质量值作为未知车辆的静态质量，此方法需要较大的计算量。

4 结 论

以车辆动态称重系统为研究对象，在分析动态称重过程力学模型的基础上，提出了1种基于神经网络预测最大超调量的动态称重计算方法，利用BP神经网络的非线性函数逼近能力，预测称重过程的位移最大超调量以及车辆的静态质量。理论分析及仿真结果表明：提出的方法所需数据量少、运算时间短，可有效地提高车辆动态称重系统的称量精度，并可克服对车辆行驶速度的限制缺陷，具有较高的实用价值。

[1]程路,张宏建,曹向辉.车辆动态称重技术[J].仪器仪表学报,2006,27(8):943-948.

[2]张瑞,吕文红.基于神经网络自适应滤波的车辆动态称重系统研究[J].公路交通科技,2010(7):160-187.

[3]WANG J F,WU M G.An overview of research on weigh-in-motion system[J].Intelligent Control andAutomation,2004(6):5241-5244.

[4]周志峰,蔡萍,陈日兴,等.基于非线性拟合的汽车动态称重数据处理新方法[J].上海交通大学学报，2006,40(5):709-712.

[5]郭兰英,梁波,董安国.汽车动态称重的新方法[J].长安大学学报：自然科学版,2009,29(2):98-100.

[6]蔡坤,陈惠滨,陈仅星.基于二阶系统的动态汽车衡称重方法及应用[J].传感技术学报，2005,18(4):906-909.

[7]蔡友发,郑惠群.车辆动态称重仪的研究与设计[J].电子测量与仪器学报,2007,21(5):100-104.

[8]贾生尧,厉志飞,章越海,等.汽车动态称重系统的信号处理研究[J].自动化仪表,2011,32(10):5-12.

[9]Shen Y,Bu Y F,Yuan M X.Study on weigh-in-motion system based on chaos immune algorithm and RBF network[C]//IEEE Pacific-Asia Workshop on Computational Intelligence and IndustrialApplication.Wuhan,China，2008,233:502-506.

[10]贾明兴,牛大鹏,王福利,等.基于RBF神经网络的非线性主元分析方法[J].仪器仪表学报，2008,29(3):453-457.

[11]周建平.具有时延的神经网络的渐近稳定性[J].安徽工业大学学报：自然科学版,2008,25(1):83-85.

[12]王文逾.基于粗糙集的分体错位式动态汽车称重系统研究[J].太原理工大学学报,2011,24(6):639-641.

[13]白瑞林,李军,白瑞祥，等.基于神经网络技术的动态定量称重控制方法的研究[J].自动化仪表，2007,21(7):1-3.

[14]郎佳红,章家岩.基于系统参数辨识汽车动态称重的技术应用的探讨[J].中原工学院学报，2008,12(6):55-59.

[15]茹秋生,庄德渊,宁宗奇.用神经网络算法降低车辆动态称重误差[J].衡器,2012,41(4):41-44.